Confira a prova resolvida do concurso dos Correios realizado em 2011.

Texto para as questões 21 e 22

Além da missão de entregar correspondências, os carteiros são também responsáveis pela difusão de importantes campanhas de conscientização da população e promoção da cidadania. Um exemplo de ação de caráter social que envolve os carteiros e que tem tido grande receptividade é o projeto Papai Noel dos Correios. Em 2009, foram adotados 21% das 1.981.000 cartas recebidas pelos Correios. O projeto contou com o apoio e a participação de 3.818 voluntários internos, 669 voluntários externos e 462 parcerias.

21) Com base no texto, é correto afirmar que, em 2009, a quantidade de cartas que não foram adotadas pelo projeto Papai Noel dos Correios foi:

A. superior a 1,2 milhão e inferior a 1,3 milhão.

B. superior a 1,3 milhão e inferior a 1,4 milhão.

C. superior a 1,4 milhão e inferior a 1,5 milhão.

D. superior a 1,5 milhão.

E. inferior a 1,2 milhão.

Resolução

Como foram adotados 21% das cartas, então não foram adotados 100 – 21 = 79% das cartas

Logo, 79% de 1.981.000 é 79/100 x 1981000 = 79 x 19810 = 1.564.990

Resposta: D

22) Se, em 2010, o projeto Papai Noel dos Correios contou com 22.435 voluntários, e se foi mantida a mesma proporção de voluntários externos e internos verificada em 2009, então a quantidade de voluntários internos em 2010 foi:

A. superior a 19.050 e inferior a 19.100.

B. superior a 19.100 e inferior a 19.150.

C. superior a 19.150.

D. inferior a 19.000.

E. superior a 19.000 e inferior a 19.050.

Resolução

Total de voluntários em 2009: 3818 + 669 = 4487

Proporção de voluntáros internos em 2009: 3818/4487

Como a proporção foi a mesma de 2009 e em 2010 foram 22435 voluntários:

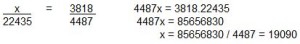
Resposta: E

23) Em 2008, nos 200 anos do Banco do Brasil, os Correios lançaram um selo comemorativo com uma tiragem de 1.020.000 unidades. No selo, cujo formato é de um retângulo medindo 40 mm × 30 mm, a estampa ocupa um retângulo que mede 35 mm × 25 mm. Dadas essas condições, é correto afirmar que a área do retângulo da estampa é

A. superior a 90% da área do retângulo do selo.

B. inferior a 75% da área do retângulo do selo.

C. superior a 75% e inferior a 80% da área do retângulo do selo.

D. superior a 80% e inferior a 85% da área do retângulo do selo.

E. superior a 85% e inferior a 90% da área do retângulo do selo.

Resolução

Como estamos trabalhando com porcentagem, não há necessidade de utilizar a medida mm.

Basta dividirmos a área da estampa pela área do selo. Veja:

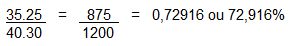
Resposta: B

24) Nos Correios, são utilizados vários tipos de caixas para o envio de encomendas, entre elas, a caixa do tipo 4B, um paralelepípedo retângulo, em papel ondulado, com arestas medindo 360 mm, 270 mm e 180 mm. O volume dessa caixa, em dm³, é:

A. superior a 18 e inferior a 21.

B. superior a 21 e inferior a 24.

C. superior a 24.

D. inferior a 15.

E. superior a 15 e inferior a 18.

Resolução

Veja em nossa sessão unidades e medidas que:

1 m = 10 dm (decímetros)

1 m = 1.000 mm (milímetros)

Primeiramente, vamos transformar as medidas das arestas para dm:

360 mm = 3,6 dm, 270 mm = 2,7 dm e 180 mm = 1,8 dm

Para calcular o volume de um paralelepípedo retângulo, basta multiplicarmos base x comprimento x altura.

Temos:

Volume = 3,6 x 2,7 x 1,8 = 17,496dm³

Resposta: E

25) Em 01/01/2011, os Correios lançaram selo comemorativo de data histórica, com tiragem de 900.000 unidades. Do dia 1 ao dia 10 de janeiro, foram vendidas 210.630 unidades desses selos, das quais 1.958 foram vendidas apenas no dia 4, primeiro dia de comercialização do selo via Internet. O prazo de comercialização desse selo pelos Correios vigorará até 31/12/2014.

Com base nas informações do texto acima e considerando-se que o ritmo de venda do selo tenha sido mantido ao longo do mês de janeiro de 2011, é correto afirmar que a quantidade de selos vendidos, em milhares de unidades, até o dia 30 do referido mês, foi:

A. superior a 640.

B. inferior a 610.

C. superior a 610 e inferior a 620.

D. superior a 620 e inferior a 630.

E. superior a 630 e inferior a 640.

Resolução

Note que o texto apresenta várias informações, a maioria irrelevante para nossa questão.

Como nos 10 primeiros dias foram comercializados 210.630 selos e o ritmo das vendas em janeiro se manteve, temos que até o dia 30 de janeiro serão comercializados 3 x 210630 = 631.890

Texto para as questões 26 e 27

Em 2/3/2011, Steve Jobs, executivo-chefe da Apple, apresentou em São Francisco o iPad2, o segundo modelo do seu tablet iPad. Lançado em abril de 2010, o iPad tornou-se o mais bem-sucedido produto eletrônico de consumo da história, com 14,8 milhões de unidades vendidas em apenas um ano. Entre as inovações presentes no iPad2, destaca-se a redução de sua espessura, que passou de 13,4 mm para 8,8 mm. O impacto do lançamento do iPad2 fez que as ações da Apple na Nasdaq, a bolsa de tecnologia de Nova York, subissem 1% no dia do lançamento, tendo alcançado 352 dólares.

26) De acordo com as informações do texto, a espessura do iPad2, em relação à espessura do iPad lançado em 2010, foi reduzida em mais de e menos de

A) mais de 1/4 e menos de 1/3.

B) mais de 1/3 e menos de 1/2 .

C) mais de 1/2.

D) menos de 1/5.

E) mais de 1/5 e menos de 1/4.

Resolução

A espessura foi reduzida em 13,4 – 8,8 = 4,6mm

Fazendo a razão entre a diferença e a espessura original, temos:

4,6 / 13,4 = 0,34

Temos:

1/3 = 0,3333 < 0,34 < 1/2 = 0,5

Resposta: B

27) Se em 1.º/3/2011, 1 dólar valia R$ 1,64, então, nessa data, de acordo com o texto, uma ação da Apple valia

A. mais de R$ 500,00 e menos de R$ 600,00.

B. mais de R$ 600,00 e menos de R$ 700,00.

C. mais de R$ 700,00 e menos de R$ 800,00.

D. mais de R$ 800,00.

E. menos de R$ 500,00.

Resolução

Note que as ações subiram 1% no dia do lançamento (02/03/11), alcançando 352 dólares.

Vamos descobrir quanto elas valiam no dia anterior.

Como aumentar 1% é a mesma coisa que multiplicar por 101/100, devemos multiplicar por 100/101 para descobrirmos o valor anterior:

352 x 100/101 = 35200/101 = 348,51 dólares

Utilizando regra de 3:

dólar ——— reais
1,00 ———- 1,64
348,51 ——– x

x = 1,64 . 348.51 = 571,55

Resposta: A

Texto para as questões de 28 a 30

O piso de uma sala retangular, medindo 3,52 m × 4,16 m, será revestido com ladrilhos quadrados, de mesma dimensão, inteiros, de forma que não fique espaço vazio entre ladrilhos vizinhos. Os ladrilhos serão escolhidos de modo que tenham a maior dimensão possível.

28) Na situação apresentada, o lado do ladrilho deverá medir

A. mais de 30 cm.

B. menos de 15 cm.

C. mais de 15 cm e menos de 20 cm.

D. mais de 20 cm e menos de 25 cm.

E. mais de 25 cm e menos de 30 cm.

Resolução

Como as respostas estão em cm, vamos considerar as medidas da sala como 352cm x 416cm.

Note que estamos querendo revestir com ladrilhos quadrados iguais de modo que não fiquem espaços vazios e que sejam os maiores possíveis. Não é difícil observar que na verdade estamos querendo achar o maior divisor comum, o popular MDC.

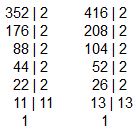
Observe que os fatores primos em comum são 2.2.2.2.2 = 32

Resposta: A

29) Se, para assentar os ladrilhos, são utilizados 2 kg de argamassa por m2  e se a argamassa é vendida em sacos de 3 kg, então a quantidade necessária de sacos de argamassa para completar o serviço é igual a:

A. 9.

B. 10.

C. 6.

D. 7.

E. 8.

Resolução

A área total é 3,52 m × 4,16 m = 14,6 m2

Como são utilizados 2kg por m2, precisamos de 2 x 14,6 = 29,2 kg.

Como cada saco possui 3kg, precisamos de 10 sacos.

Resposta: B

30) ANULADA

Texto para as questões 31 e 32

Para o envio de pequenas encomendas, os Correios comercializam caixas de papelão, na forma de paralelepípedo retângulo, de dois tipos: tipo 2, com arestas medindo 27 cm, 18 cm, e 9 cm; e tipo 4, com arestas medindo 36 cm, 27 cm e 18 cm.

31) Se um escritor deseja enviar livros de sua autoria a outro estado e se cada livro mede 23 cm × 16 cm × 1,2 cm, então a quantidade máxima desses livros que poderá ser enviada em uma caixa do tipo 2, sem que sejam danificados ou deformados, é igual a

A. 9.

B. 5.

C. 6.

D. 7.

E. 8.

Resolução

Note que o comprimento e a largura dos livros cabem perfeitamente na caixa tipo 2.

Como a espessura dos livros é de 1,2cm e a espessura da caixa é de 9cm. Temos:

9 / 1,2 = 7,5

Como não podemos enviar meio livro, a caixa cabe 7 livros.

Resposta: D

32) Se o valor de comercialização de cada tipo de caixa for proporcional ao seu volume e se uma caixa do tipo 2 custar

R$ 4,50, então uma caixa do tipo 4 custará

A. R$ 16,00.

B. R$ 18,00.

C. R$ 20,00.

D. R$ 22,00.

E. R$ 14,00.

Resolução

Volume da caixa tipo 2 = 27 x 18 x 9

Volume da caixa tipo 4 = 36 x 27 x 18

Como o 27 e o 18 se repetem e 36 é 4 x 9, a caixa tipo 4 é 4x maior do que a caixa tipo 2.

Logo, a caixa tipo 4 custará 4 x 4,50 = 18 reais

Resposta: B

33) Em um bairro onde as casas foram todas construídas de acordo com um projeto padrão, os lotes têm 12 metros de frente, em cada lote a caixa de correspondências fica sempre na mesma posição e os postes de iluminação pública são espaçados em 50 metros. O carteiro que entrega correspondências nesse bairro percebeu que a caixa de correspondências da primeira casa de uma rua bastante longa fica exatamente atrás de um poste de iluminação. Nesse caso, caminhando nessa rua e desconsiderando os possíveis espaços entre dois lotes vizinhos, até que encontre a próxima caixa de correspondências atrás do poste de iluminação, o carteiro deverá percorrer uma distância igual a

A. 210 metros.

B. 255 metros.

C. 300 metros.

D. 120 metros.

E. 165 metros.

Resolução

Note que queremos conhecer quando um multiplo de 12 coincidirá com um múltiplo de 50, ou seja, o mínimo múltiplo comum, popular mmc.

Resposta: C

34) Das correspondências que deveria entregar, o carteiro Carlos passou 7/10 delas para o carteiro Jorge; dessas, Jorge repassou 3/5 para o carteiro Marcos. Nesse caso, com relação à quantidade de correspondência que Carlos deveria entregar, a quantidade que coube a Marcos é igual a:

A. 3/10

B. 2/5

C. 21/50

D. 10/15

E. 1/10

Resolução

Carlos passou 7/10 delas para o carteiro Jorge que repassou 3/5 para o carteiro Marcos.

Basta nortar que Marcos ficou com 3/5 de 7/10 das cartas que Carlos deveria entregar, logo:

Marcos ficou com:

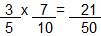
das cartas de Carlos.

Resposta: C

35) Se a agência dos Correios de uma pequena cidade presta, diariamente, 40 atendimentos em média, e se, em razão de festas na cidade, a média de atendimentos diários passar a 52, então, nesse caso, haverá um aumento percentual de atendimentos de

A. 40%.

B. 52%.

C. 90%.

D. 12%.

E. 30%.

Resolução

Note que a média aumentou em 12. Calculando a porcentagem:

12 / 40 = 0,3 ou 30%

Resposta: E

Texto para as questões 36 e 37

As tarifas dos serviços postais e telegráficos, nacionais e internacionais, prestados pelos Correios sofrerão reajuste, conforme portaria assinada pelo ministro interino da Fazenda e publicada no Diário Oficial da União. Os novos valores já foram anunciados pelo Ministério da Fazenda, mas ainda não podem ser cobrados, pois devem ser aprovados pelo Ministério das Comunicações. O primeiro porte da carta não comercial (pessoa física), segundo o Ministério da Fazenda, terá o valor elevado de R$ 0,70 para até R$ 0,75, com um crescimento de até 7,14%. O primeiro porte da carta comercial (pessoa jurídica) terá o valor reajustado de R$ 1,05 para até R$ 1,10, com uma variação de 4,76%, se implementado o reajuste em sua totalidade. O primeiro porte do chamado franqueamento autorizado de cartas (FAC), que é um contrato para a remessa de grandes quantidades de cartas comerciais, passará de R$ 0,92 para até R$ 0,98, um crescimento de 6,52%, se totalmente implementado o reajuste. O preço mínimo dos telegramas nacionais contratados nas agências dos Correios, sem contar a taxação do imposto sobre circulação de mercadorias e serviços (ICMS) estadual, subirá de R$ 6,30 para até R$ 6,70, um aumento de 6,34%. O preço do telegrama internacional também subirá. O valor mínimo por palavra avançará de R$ 0,80 para até R$ 0,85, um reajuste de 6,25%, se integralmente implementado.

36) Caso os referidos reajustes atinjam os valores máximos indicados no texto, entre os serviços postais e telegráficos, aquele que terá o maior reajuste relativo será o

A. primeiro porte da carta comercial (pessoa jurídica).

B. primeiro porte do FAC.

C. telegrama nacional.

D. telegrama internacional.

E. primeiro porte da carta não comercial (pessoa física).

Resolução

Maior reajuste relativo refere-se a maior porcentagem, ou seja, 7,14% (carta não comercial pessoa física)

Resposta: E

37) Caso os reajustes mencionados no texto sejam aprovados daqui a exatamente três meses, o aumento máximo previsto para o primeiro porte do FAC corresponderá a uma taxa de juros simples mensal de:

A. 2,11%.

B. 2,17%.

C. 2,38%.

D. 1,59%.

E. 2,08%.

Resolução

Como o aumento seria de 6,52% e queremos saber a taxa de juros simples mensal, basta dividirmos pelos 3 meses.

 6,52 / 3 = 2,17%

Resposta: B

Texto para as questões 38 e 39

O cálculo do preço para o envio de encomendas por SEDEX depende das localidades de origem e destino e da massa da encomenda. Fixados a origem e o destino, o valor é calculado somando-se uma parcela fixa a uma quantia proporcional à massa da encomenda, medida em quilogramas.

38) Suponha que, no envio, por SEDEX, de encomendas entre as cidades de São Paulo – SP e Rio Branco – AC, a parcela fixa seja de R$ 35,10 e a constante de proporcionalidade, R$ 13,20. Com base nessa situação, considere o envio, por SEDEX, de duas encomendas de 3 kg cada uma e quatro encomendas de 2 kg cada uma, todas para pessoas diferentes, de São Paulo para Rio Branco. Assinale a opção correspondente à expressão numérica que representa o valor a ser pago pelo envio dessas encomendas.

A. [35,10 + 13,20 × 3] × 2 + [35,10 + 13,20 × 2] × 4

B. [35,10 + 13,20] × 3 × 2 + [35,10 + 13,20] × 2 × 4

C. [35,10 + 13,20 × 3] + [35,10 + 13,20 × 2]

D. [35,10 + 13,20] × [3 × 2 + 2 × 4]

E. 35,10 × 3 × 2 + 13,20 × 2 × 4

Resolução

O texto e o enunciado nos informam que para enviar uma encomenda, paga-se R$ 35,10 fixos e R$ 13,20 a cada kg.

Para enviar dois pacotes de 3kg:  2 x (35,10 + 13,20 × 3)
Somando os dois temos a letra A

Para enviar quatro pacotes de 2kg:  4 x (35,10 + 13,20 × 2)

39) Matheus pagou R$ 26,80 para enviar, de Brasília – DF a São Paulo – SP, uma encomenda de 1 kg, e Lucas pagou R$ 31,40 pelo envio, de Brasília a São Paulo, de uma encomenda de 2 kg. Nesse caso, a parcela fixa cobrada pelo envio de encomendas de Brasília para São Paulo é igual a

A. R$ 22,00.

B. R$ 21,80.

C. R$ 21,60.

D. R$ 21,40.

E. R$ 22,20.

Vamos considerar x = valor fixo e y = valor proporcional. Temos o seguinte sistema de equações:

Matheus:  x + y = 26,80    <=>  y = 26,80 – x

Lucas:      x + 2y = 31,40

Substituindo a equação de Matheus na de Lucas:

x + 2(26,80 – x) = 31,40

x + 53,60 – 2x = 31,40

x – 2x = 31,40 – 53,60

x = 22,20

40) Considere que 12 carteiros levem 21 minutos na triagem de certa quantidade de correspondências e que todos os carteiros trabalhem com a mesma eficiência. Nesse caso, se a esses carteiros forem agrupados outros dois, com igual eficiência, então o tempo necessário para a triagem da mesma quantidade de correspondências será igual a

A. 19 minutos.

B. 18 minutos.

C. 15 minutos.

D. 14 minutos.

E. 12 minutos.

Como ao aumentando-se a quantidade de carteiros, diminui-se o tempo, vamos utilizar regra de 3 simples inversa:

     carteiros            minutos

          12                     21                    14x = 21.12

          14                      x                         x = 252 / 14 = 18 minutos