Estudando matemática para concursos? Confira aqui a prova resolvida do concurso da PRF realizado em 2013 pelo Cespe.

Veja também em nosso menu provas resolvidas referente a outros concursos da PRF e de outras carreiras policiais.

Bom estudo!

 

 

Considerando que uma equipe de 30 operários, igualmente produtivos, construa uma estrada de 10 km de extensão em 30 dias, julgue os próximos itens.

 

16. Se, ao iniciar a obra, a equipe designada para a empreitada receber reforço de uma segunda equipe, com 90 operários igualmente produtivos e desempenho igual ao dos operários da equipe inicial, então a estrada será concluída em menos de 1/5 do tempo inicialmente previsto.

 

Resolução

Primeiro vamos arrumar os dados do problema para utilizarmos regra de três.

Obs: Quanto mais operários, menos dias para a realização da obra, ou seja, temos grandezas inversamente proporcionais.

 

Multiplicando em linha reta:

x.120 = 30.30

120x = 900

x = 900/120

x = 7,5 dias

 

Tempo inicialmente previsto:

30 . 1/5 = 6 dias

Reposta: ERRADA.

 

 

17. Se a tarefa estiver sendo realizada pela equipe inicial de 30 operários e, no início do quinto dia, 2 operários abandonarem a equipe, e não forem substituídos, então essa perda ocasionará atraso de 10 dias no prazo de conclusão da obra.

 

Resolução

Vamos ser mais pessimistas e considerar que os dois pedreiros nunca foram a obra.

Quanto mais operários, menos dias.

28x = 30.30

28x = 900

x = 900/28

x = 32,14 dias

 

28 pedreiros geram um atraso de 2,14 dias.

Questão FALSA.

 

 

 

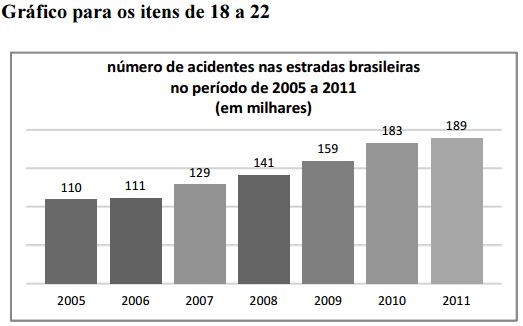
18. A média do número de acidentes ocorridos no período de 2007 a 2010 é inferior à mediana da sequência de dados apresentada no gráfico.

 

Resolução

Primeiramente, vamos calcular a média de acidentes de 2007 a 2010:

Média = (129 + 141 + 159 + 183)/4

Média = 153

 

Relembrando, a mediana é o número que se encontra na posição central quando todos estão em ordem numérica.

Obs: Quando a quantidade de elementos é par, devemos tirar a média aritmética dos dois centrais.

Mediana = (141 + 159)/2

Mediana = 150

 

A questão é FALSA.

 

 

19. Os valores associados aos anos de 2008, 2009 e 2010 estão em progressão aritmética.

 

Resolução

Temos:

2008: 141.000

2009: 159.000

2010: 183.000

 

Lembrando que uma progressão aritmética é uma sequência onde a diferença entre dois elementos consecutivos é sempre igual, fato que não está ocorrendo:

159.000 – 141.000 = 18.000

183.000 – 159.000 = 24.000

A questão é FALSA.

 

 

20. O número de acidentes ocorridos em 2008 foi, pelo menos, 26% maior que o número de acidentes ocorridos em 2005.

De 2005 a 2008 tivemos um aumento de 141 – 110 = 31

Daí, 31/110 = 0,2818 = 28,18%

A questão está CORRETA.

 

 

Considere que, em 2009, tenha sido construído um modelo linear para a previsão de valores futuros do número de acidentes ocorridos nas estradas brasileiras. Nesse sentido, suponha que o número de acidentes no ano t seja representado pela função F(t) = At + B, tal que F(2007) = 129.000 e F(2009) =159.000. Com base nessas informações e no gráfico apresentado, julgue os itens a seguir.

 

21. O valor da constante A em F(t) é superior a 14.500.

 

Resolução

Basta observar que temos uma função afim, onde sabemos dois pontos, assim fica fácil descobrir os valores de A e B.

1) 129000 = 2007A + B

2) 159000 = 2009A + B

 

1) 129000 – 2007A = B

2) 159000 – 2009A = B

 

Daí,

129000 – 2007A = 159000 – 2009A

2009A – 2007A = 159000 – 129000

2A = 30000

A = 30000/2 = 15000

Questão CORRETA

 

 

22. A diferença entre a previsão para o número de acidentes em 2011 feita pelo referido modelo linear e o número de acidentes ocorridos em 2011 dado no gráfico é superior a 8.000.

 

Resolução

Como já sabemos o valor de A, vamos agora descobrir o valor de B:

F(2009) = 159000

159000 = 2009A + B

159000 = 2009.15000 + B

B = 159000 – 30135000

B = – 29976000

 

Temos então que nossa função é:

F(t) = 15000t – 29976000

F(2011) = 15000.2011 – 29976000

F(2011) = 189000

 

Analisando o gráfico, é possível verificar que o modelo calculou a quantidade exata de acidentes, ou seja, a diferença não foi superior a 8.000 acidentes.

Questão ERRADA.

 

 

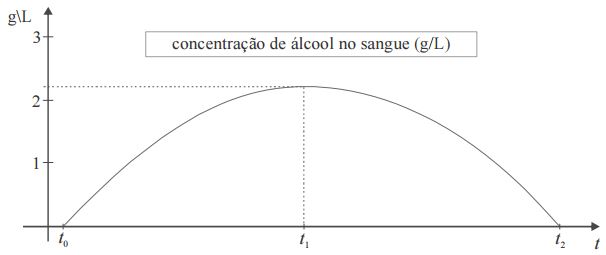
Considere que o nível de concentração de álcool na corrente sanguínea, em g/L, de uma pessoa, em função do tempo t, em horas, seja expresso por N = – 0,008(t² – 35t + 34). Considere, ainda, que essa pessoa tenha começado a ingerir bebida alcoólica a partir de t = t0 (N(t0 = 0), partindo de um estado de sobriedade, e que tenha parado de ingerir bebida alcoólica em t = t1, voltando a ficar sóbria em t = t2. Considere, por fim, a figura acima, que apresenta o gráfico da função N(t) para t є [t0, t2]. Com base nessas informações e tomando 24,3 como valor aproximado de √589, julgue os itens que se seguem.

 

23. O nível de concentração de álcool na corrente sanguínea da pessoa em questão foi superior a 1 g/L por pelo menos 23 horas.

 

Resolução

Isso ocorre quando:

– 0,008(t² – 35t + 34) > 1

– 8(t² – 35t + 34) > 1000

t² – 35t + 34 > – 125

t² – 35t + 159 > 0

 

Δ = b² – 4ac

Δ = 35² – 4.1.159

Δ = 589

 

t = (-b +- √Δ)/2a

t = (35 +- √589)/2.1

t = (35 +- 24,3)/2

 

t’ = (35 + 24,3)/2 = 29,65

t” = (35 – 24,3)/2 = 5,35

 

Calculando a diferença:

29,65 – 5,35 = 24,3

Questão CERTA.

 

 

 

24. O valor de t2 é inferior a 36.

 

Resolução

Só acharmos as raízes da função:

-0,008(t² – 35t + 34) = 0 (x 1000)

-8(t² – 35t + 34) = 0 (: -8)

t² – 35t + 34 = 0

t0 = 1 ou t2 = 34

Questão CERTA.

 

 

25. O nível de concentração mais alto de álcool na corrente sanguínea da referida pessoa ocorreu em t = t1, com t1 > 18 horas.

 

Resolução

O nível mais alto, em se tratando de uma função do segundo grau, é exatamente no meio das duas raízes, ou seja, basta tirar a média aritmética de 1 e 34, que é igual a 35/2 = 17,5

Questão ERRADA.

 

 

Gostou da prova resolvida da PRF 2013?

Deixe o seu comentário.