Estudando matemática e raciocínio lógico para concursos? Confira aqui a prova resolvida do concurso para a Polícia Rodoviária Federal (PRF) realizado em 2008 pelo Cespe.
Lembrando que você encontrará outras provas resolvidas de carreiras policiais em nosso menu.
Bom estudo!
Questão 11. Em um posto de fiscalização da PRF, cinco veículos foram abordados por estarem com alguns caracteres das placas de identificação cobertos por uma tinta que não permitia o reconhecimento, como ilustradas abaixo, em que as interrogações indicam os caracteres ilegíveis.
Os policiais que fizeram a abordagem receberam a seguinte informação: se todas as três letras forem vogais, então o número, formado por quatro algarismos, é par. Para verificar se essa informação está correta, os policiais deverão retirar a tinta das placas:
a) I, II e V
b) I, III, e IV
c) I, III, e V
d) II, III, e IV
e) II, IV e V
Resolução
A única maneira da informação estar errada é se alguma placa apresentar as três letras vogais e o último número par.
Placa 1: Possui três vogais, logo os policiais precisam verificar se o último número realmente é par.
Placa 2: Não possui somente vogais, logo é irrelevante o último número ser par.
Placa 3: Existe a possibilidade de possuir três vogais e o último número ser par. Os policiais deverão verificar.
Placa 4: Como o último número já é par, é irrelevante saber se as letras são vogais.
Placa 5: Devemos verificar se a última letra é vogal, pois em caso positivo a informação seria falsa.
Questão 12. Em um posto de fiscalização da PRF, os veículos A, B e C foram abordados, e os seus condutores, Pedro, Jorge e Mário, foram autuados pelas seguintes infrações:
(i) um deles estava dirigindo alcoolizado;
(ii) outro apresentou a CNH vencida;
(iii) a CNH apresentada pelo terceiro motorista era de categoria inferior à exigida para conduzir o veículo que ele dirigia.
Resolução
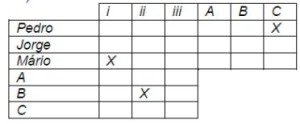
Sabe-se que Pedro era o condutor do veículo C; o motorista que apresentou a CNH vencida conduzia o veículo B; Mário era quem estava dirigindo alcoolizado. Com relação a essa situação hipotética, julgue os itens que se seguem. Caso queira, use a tabela na coluna de rascunho como auxílio.
I – A CNH do motorista do veículo A era de categoria inferior à exigida.
II – Mário não era o condutor do veículo A.
III – Jorge era o condutor do veículo B.
IV – A CNH de Pedro estava vencida.
V – A proposição “Se Pedro apresentou CNH vencida, então Mário é o condutor do veículo B” é verdadeira.
Estão certos apenas os itens
a) I e II
b) I e IV
c) II e III
d) III e V
e) IV e V
Resolução
Se Pedro dirigia o veículo C e o que estava com CNH vencida era o de B, como Mário estava alcoolizado, ele não estava nos veículos B e C, logo estava em A.
Se Pedro dirigia C e Mário A, então Jorge dirigia B e estava com a CNH vencida.
Logo, sobra a Pedro estar com a CNH com categoria inferior ao exigido.
Para um melhor entendimento, sugerimos completar a tabela a cada linha de raciocínio.
Texto para as questões de 13 a 16
Ficou pior para quem bebe.
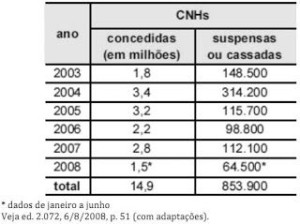
O governo ainda espera a consolidação dos dados do primeiro mês de aplicação da Lei Seca para avaliar seu impacto sobre a cassação de CNHs. As primeiras projeções indicam, porém, que as apreensões subirão, no mínimo, 10%. Antes da vigência da Lei Seca, eram suspensas ou cassadas, em média, aproximadamente 155.000 CNHs por ano. Se as previsões estiverem corretas, a média anual deve subir para próximo de 170.000. A tabela a seguir mostra esses resultados nos últimos anos( fonte: DENATRAN ).
Questão 13. Para que a média de CNHs suspensas ou cassadas, de 2003 a 2008, atinja o valor previsto de 170.000, será necessário que, em 2008, a quantidade de CNHs suspensas ou cassadas seja um número
A) inferior a 180.000.
B) superior a 180.000 e inferior a 200.000.
C) superior a 200.000 e inferior a 220.000.
D) superior a 220.000 e inferior a 240.000.
E) superior a 240.000
Resolução
Para fazer a média dos 6 anos, devemos observar que em 2008 temos dados até junho. Vamos chamar de x o número de CNH cassadas ou suspensas de julho a dezembro e calcular a média:
(853900 + x) / 6 = 170000
853900 + x = 6.170000
853900 + x = 1020000
x = 1020000 – 853900 = 166100
Logo, 166100 + 64500 = 230600
Questão 14. Suponha que, em 2006, nenhuma CNH tenha sofrido simultaneamente as penalidades de suspensão e de cassação e que, nesse mesmo ano, para cada 5 CNHs suspensas, 3 eram cassadas. Nessa situação, é correto afirmar que a diferença entre o número de CNHs suspensas e o número de CNHs cassadas é:
A) inferior a 24.000.
B) superior a 24.000 e inferior a 25.000.
C) superior a 25.000 e inferior a 26.000.
D) superior a 26.000 e inferior a 27.000.
E) superior a 27.000
Resolução
O número de carteiras suspensas ou cassadas em 2006 foi de 98800.
Note que neste período, 5/8 das carteiras foram suspensas e 3/8 foram cassadas, logo a diferença é de 2/8:
Questão 15. Supondo que, neste ano de 2008, a variação na quantidade de CNHs emitidas de um mês para o mês anterior seja mantida constante e que, em fevereiro de 2008, tenham sido emitidas 175.000 habilitações, então o total de habilitações emitidas em 2008 será, em milhões,
A) inferior a 3.
B) superior a 3 e inferior a 3,5.
C) superior a 3,5 e inferior a 4.
D) superior a 4 e inferior a 4,5.
E) superior a 4,5.
Resolução
Como a variação é constante, vamos assumir que a cada mês aumenta x, e como em fevereiro foram emitidas 175000 habilitações, temos:
(175000 – x) + (175000) + (175000 + x) + (175000 + 2x) + (175000 + 3x) + (175000 + 4x) = 1500000
1050000 + 9x = 1500000
9x = 450000
x = 50000
Veja que temos uma PA: 125000, 175000, 225000, …
a12 = 125000 + 11.50000 = 675000
Questão 16. Considerando que, em 2005, o motivo de todas as cassações ou suspensões de CNH tenha sido dirigir veículo automotor depois de ingerir bebida alcoólica em quantidade superior à permitida, e que uma pesquisa tenha revelado que 12% da população brasileira admitia dirigir veículo automotor depois de ingerir bebida alcoólica em quantidade superior à permitida, e considerando, também, que a quantidade de CNHs cassadas ou suspensas corresponda, proporcionalmente, a 3 em cada 600 indivíduos que admitiam dirigir veículo automotor depois de ingerir bebida alcoólica em quantidades superior à permitida, é correto inferir que, em 2005, a população brasileira era, em milhões:
a) inferior a 180.
b) superior a 180 e inferior a 185.
c) superior a 185 e inferior a 190.
d) superior a 190 e inferior a 195.
e) superior a 195.
Resolução
O número de carteiras cassadas ou suspensas em 2005 foi de 115700.
Considere x = população que dirige embriagada no Brasil. Temos:
3x = 600.115700
3x = 69420000
x = 69420000 / 3 = 23140000
Esse número representa 12% da população brasileira (y), logo:
Questão 17. ANULADA
Questão 18.
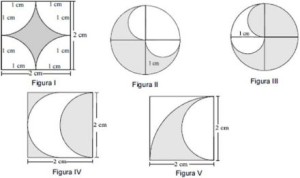
Considerando, em relação às figuras ao lado, que, na figura I, as 4 curvas são quartos de circulo; nas figuras II, III e IV, as curvas são 2 semicírculos; na figura V, aparece 1 quarto de círculo e, interno a ele, um semicírculo, nessa situação, as figuras em que as partes sombreadas têm áreas iguais são:
a) I e IV.
b) I e V.
c) II e III.
d) II e V.
e) III e IV
Resolução
Figura I:
Temos um quadrado com 4 semicírculos inscritos, que resultam em um círculo completo. Então a área sombreada será a área do quadrado menos a área do círculo com raio de 1 cm. Calculando as áreas:
1. Área do quadrado: 2 x 2 = 4 cm²;
2. Área do círculo: ∙π 1² = π cm²;
3. Área sombreada: 4 – π.
Figura II:
A área sombreada é formada por 3/4 da área de um círculo com raio de 1 centímetro, menos a área de 2 semicírculos de raio igual a 1/2 centímetro. Lembre que dois semicírculos formam um círculo. Então:
1. Área do círculo com raio de 1 cm: π 1² = π cm²;
2. 3/4 da área do círculo anterior: 3π/4
3. Área do círculo com raio igual de 1/2 cm: π.(1/2)² = π/4
4. Área sombreada: 3π/4 – π/4 = 2π/4 = π/2cm².
Figura III:
Se o semicírculo sombreado trocar de lugar com o semicírculo brando, a área sombreada será igual a 3/4 da área do círculo de raio de 1 cm. Veja:
1. Área do círculo de raio de 1 cm: π1² = π cm²;
2. Área sombreada: 3π/4 cm².
Figura IV
Se encaixarmos o semicírculo sombreado no semicírculo branco, têm-se um retângulo com a metade sombreada e a outra branca. Dessa forma, a área sombreada seria igual a metade da área de um retângulo de 2 x 2. Veja:
1. Área sombreada: 2.2/2 = 2 cm².
Figura V:
A área sombreada será obtida com a subtração da área de um quarto de círculo de raio igual a 2 centímetro pela metade de um semicírculo de raio igual a 1 centímetro. Calculando as áreas:
1. Área de 1/4 de círculo de 2 cm de raio: π2²/4 = πcm².
2. Área de um semicírculo de 1 cm de raio: π1²/2 = π/2cm².
3. Área sombreada: π – π/2 = π/2 cm².
Questão 19. No ano de 2006, um indivíduo pagou R$ 4.000,00 pelas multas de trânsito recebidas, por ter cometido várias vezes um mesmo tipo de infração de trânsito, e o valor de cada uma dessas multas foi superior a R$ 200,00. Em 2007, o valor da multa pela mesma infração sofreu um reajuste de R$ 40,00, e esse mesmo indivíduo recebeu 3 multas a mais que em 2006, pagando um total de R$ 6.720,00.
Vamos agora analisar cada uma das alternativas.
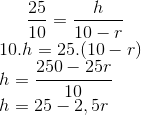
(o fato de -2,5r ser negativo nos prova que a função afim é decrescente)
b) O volume do cilindro como uma função de r é uma função quadrática.
Gostou da prova resolvida da PRF 2008?
Deixe o seu comentário.

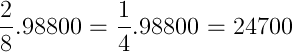
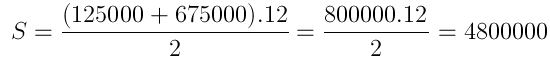
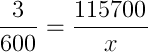
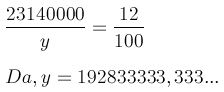
Nao entendo a questão 20 a ultima questão. Na letra A), você igualou o raio do cilindro a 10-r, como pode ser??? Se somente o segmento restante pode ser denominado assim. Uma vez que r é o raio do cilindro, então o que SOBRA é 10-r para quando somar voltar o valor 10. Só não entendi isso. Por favor me explique!
Gabriel, 10-r não é o raio do cilindro, é o lado do triângulo menor quando utilizamos a semelhança de triângulos.