Confira aqui a prova resolvida do concurso para a Polícia Militar do Estado do Paraná (PR) realizado em 2010.
Bom estudo!
11. Sejam quatro cidades designadas por A, B, C e D. Considere que há três rodovias que ligam a cidade A com a cidade B, duas rodovias que ligam a cidade B com a cidade C e quatro rodovias que ligam a cidade C com a cidade D.
Se desejamos ir de A até D, passando pelas cidades B e C, de quantas formas poderemos realizar tal percurso?
a) 12
b) 16
c) 24
d) 30
e) 36
Resolução
3 (A até B) x 2 (B até C) 4 x (C até D) = 3 x 2 x 4 = 24
Resposta: C
12. Considere uma colisão de dois veículos. Num sistema de coordenadas cartesianas, as posições finais destes veículos após a colisão são dadas nos pontos A = (2,2) e B = (4, 1). Para compreender como ocorreu a colisão é importante determinar a trajetória retilínea que passa pelos pontos A e B. Essa trajetória é dada pela equação:
a) x – y = 0
b) x + y – 5 = 0
c) x – 2y + 2 = 0
d) 2x + 2y – 8 = 0
e) x + 2y – 6 = 0
Resolução
Devemos calcular o determinante entre os pontos P(x,y), A(2,2) e B(4,1):
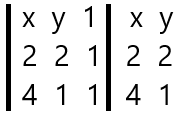
Fazendo o produto das diagonais principais menos o produto das diagonais secundárias:
2x + 4y + 2 – 8 – x – 2y = 0
x + 2y – 6 = 0
Resposta: E
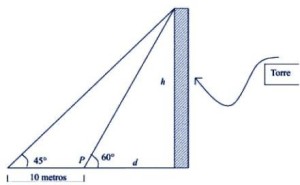
13. Uma torre de observação é construída em uma região plana. Um bombeiro precisa determinar aaltura h da torre. Ele observa a torre sob um ângulo de 60°, a partir de um ponto P, situado a d metrosdesta. Partindo de P, ao se afastar da torre por mais 10 metros, passa a vê-la sob um ângulo de 45°.Qual a altura da torre, em metros?
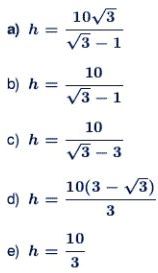
Resolução
Triangulo com ângulo de 60 graus
tg60 = h/d
√ 3 = h/d
d = h / √ 3 (1)
Triângulo com ângulo de 45 graus
tg45 = h/(d+10)
1 = h/(d+10)
h = d + 10 (2)
Substituindo (1) em (2):
h = h / √ 3 + 10 (multiplicar por √ 3)
h√ 3 = h + 10√ 3
h√ 3 – h = 10√ 3
h(√ 3 – 1) = 10√ 3
h = 10√ 3 / (√ 3 – 1)
Resposta: A

15. Considere as afirmativas:
I- A função logarítmica na base 2, para x>0 é sempre positiva.
II- A função logarítmica natural f(x) = ln(x), para x>0 é sempre crescente.
III- A função cosseno f(x) = cos(x), para x>0, é sempre positiva.
IV- A função tangente, f(x) = tg(x), para 0 < x < π/2, é sempre crescente.
Quais as únicas alternativas corretas?
a) I e II
b) II e IV
c) III e IV
d) I, II e III
e) I, III e IV
Resolução
I) Falsa. Será negativa quando 0 < x < 1.
II) Verdadeira. O número de Euler é aproximadamente 2,718 > 1, fazendo com que a função seja crescente para x > 0.
III) Falsa. A função Cosseno varia entre 1 e -1
IV) Verdadeira. A função tangente é sempre crescente para x > 0.
Resposta: B
16. Um serralheiro precisa estimar o custo de estruturas de alumínio no formato de polígonos. Essas estruturas poligonais devem ter barras diagonais para reforçá-las. O custo da estrutura metálica depende do número de barras diagonais. O número de diagonais d de um polígono de n lados é dado por uma função quadrática. Vejamos, o triângulo tem n = 3 lados e d = O diagonais, o quadrado tem n = 4 lados e d = 2 diagonais, o pentágono tem n = 5 lados e d = 5 diagonais e assim por diante. Generalizando, em um polígono de n lados, o número de diagonais d é dado por:
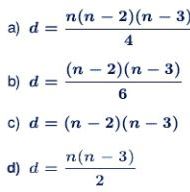
Resolução
A fórmula foi obtida:
– descontando de n os 3 vértices para onde não podem ser traçadas diagonais (os 2 adjacentes e ele mesmo): n – 3;
– multiplicando o resultado obtido pelo número de vértices: n . (n – 3);
– dividindo o resultado obtido por 2, devido às diagonais consideradas duas vezes.
Resposta: D
17. Três números estão em uma progressão aritmética (PA) crescente. O produto dos três é 66 e a soma deles é 18. Determine o próximo termo dessa progressão aritmética.
a) a4 = 12
b) a4 = 13
c) a4 = 14
d) a4 = 15
e) a4 = 16
Resolução
Observe que podemos representar os três números por x-r, x, x+r, onde r = razão.
Temos:
x – r + x + x + r = 18
3x = 18
x = 18/3
x = 6
(x – r).x.(x + r) = 66
(6 – r).6(6 + r) = 66
(36 – r²).6 = 66
216 – 6r² = 66
6r² = 216 – 66
6r² = 150
r² = 150/6
r² = 25
r = 5
Logo,
a3 = 6 + 5 = 11
a4 = 11 + 5 = 16
Resposta: E
18) Considere o sistema linear a seguir:
2ax + 2y = 2 (1)
3x + 3y = b (2)
Para quais valores dos parâmetros a e b o sistema tem solução x e y única?
a) a = 1 e b = 2
b) a = 1 e b ≠ 2
c) a qualquer e b ≠ 2
d) a ≠ 1 e b qualquer
e) a qualquer e b = 2
Resolução
Multiplicando (1) por 1,5 e subtraindo (2):
(3a – 3)x + (3 – 3)y = 2 – b
x = (2 – b)/(3a – 3)
Note que b pode assumir qualquer valor enquanto a não pode ser igual a 1.
Resposta: D
19. Considere uma placa de trânsito na forma de um hexágono regular com lados de L centímetros. Sabe-se que um hexágono regular de lados L é formado por seis triângulos equiláteros de lados L. Como a leitura desta sinalização (placa) depende da área A da placa, temos que A, em função do comprimento L, é dada por:
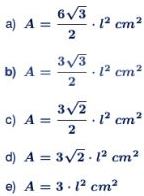
Resolução
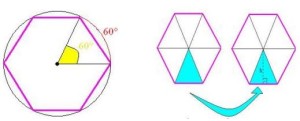
Primeiramente, a área do hexagono é 6x a área do triângulo.
Aplicando o Teorema de Pitágoras, vamos descobrir a altura h do triângulo para descobrirmos sua área:
l² = h² + (l/2)²
l² – l²/4 = h²
(4l² – l²)/4 = h²
3l²/4 = h²
h = l√3/2
Calculando a área:
A∆ = l . l√3/2/2
A∆ = l² √3 /4
A área do hexágono regular será igual a 6 vezes a área do triângulo equilátero.
A = 6 . l² √3/4
A = 3 l² √3 / 2
Resposta: B
20) Qual deve ser o capital inicial que um cidadão deve aplicar em um fundo de renda fixa, que utiliza o sistema de juros compostos e que rende 20% ao ano, de modo que ele tenha R$ 1.440,00 ao final de dois anos?
a) R$ 960,00
b) R$ 975,00
c) R$ 1.000,00
d) R$ 1.003,00
e) R$ 1.010,00
Resolução
Utilizando a fórmula de juros compostos:

Resposta: C
Gostou da prova resolvida da PM Paraná 2010?
Deixe o seu comentário.
