Confira aqui a prova resolvida do concurso para o Tribunal de Justiça do Estado do Rio Grande do Sul, realizado em 2012 pela FAURGS (TJ RS 2012).

O concurso é muito disputado e uma dica que sempre vale a pena é conferir o que caiu na última prova.

Bom estudo!

 

 

Questão 27. Os 20 candidatos aprovados em um concurso do Tribunal de Justiça serão colocados em 10 gabinetes de desembargadores. Se cada gabinete receber pelo menos um dos candidatos aprovados e cada um deles só puder ser lotado em um único gabinete, pode-se afirmar que

a) pelo menos um dos gabinetes receberá dois dos candidatos aprovados.

b) nenhum gabinete receberá mais de dois candidatos aprovados.

c) cada gabinete receberá dois candidatos aprovados.

d) pelo menos um dos gabinetes receberá dois ou mais candidatos aprovados.

e) haverá gabinetes que receberão, cada um, apenas um dos candidatos aprovados.

 

Resolução

Sabendo que cada gabinete receberá pelo menos um dos 20 candidatos, vamos analisar cada uma das opções:

 

A hipótese de colocarmos apenas 1 candidato em 9 gabinetes, e 11 candidatos no gabinete restante já descarta as opções A, B e C.

Se os candidatos forem divididos igualmente entre os gabinetes, eliminamos a opção E.

A resposta é a letra D, que pelo Princípio da Casa dos Pombos, não é possível deixar algum gabinete sem dois ou mais candidatos.

 

Resposta: D

 

 

Questão 28. Observando-se, durante certo período, o trabalho de 24 desenhistas do Tribunal de Justiça, verificou-se que 16 executaram desenhos arquitetônicos, 15 prepararam croquis e 3 realizaram outras atividades. O número de desenhistas que executaram desenho arquitetônico e prepararam croquis, nesse período, é de

a) 10

b) 11

c) 12

d) 13

e) 14

 

Resolução

Retirando os 3 que realizaram outras atividades, temos que 21 desenhistas realizaram projetos arquitetônicos (16) ou fizeram croquis (15).

Quando somamos 16 + 15 = 31, podemos perceber que 10 fizeram as duas coisas, já que estamos analisando um universo de 21 desenhistas.

 

Resposta: A

 

 

Questão 29. Um técnico judiciário deve agrupar 4 processos do juiz A, 3 do juiz B e 2 do juiz C, de modo que os processos de um mesmo juiz fiquem sempre juntos e em qualquer ordem. A quantidade de maneiras diferentes de efetuar o agrupamento é de

a) 32

b) 38

c) 288

d) 864

e) 1728

 

Resolução

Existem 3 grupos de processos. Um para cada juiz.

Esses grupos podem ser organizados de 6 maneiras diferentes:

3 x 2 x 1 = 6

 

Os 4 processos do juiz A podem ser organizados de 24 maneiras diferentes:

4 x 3 x 2 x 1 = 24

 

Os 3 processos do juiz B podem ser organizados de 6 maneiras diferentes:

3 x 2 x 1 = 6

 

Os 2 processos do juiz C podem ser organizados de 2 maneiras diferentes:

2 x 1 = 2

 

Quantidade total:

6 x 24 x 6 x 2 = 1728

 

Resposta: E

 

 

Questão 30. O Tribunal de Justiça está utilizando um código de leitura de barras composto por 5 barras para identificar os pertences de uma determinada seção de trabalho. As barras podem ser pretas ou brancas. Se não pode haver código com todas as barras da mesma cor, o número de códigos diferentes que se pode obter é de

a) 10

b) 30

c) 50

d) 150

e) 250

 

Resolução

São 5 barras, com duas opções de cor. A quantidade possível é:

2 x 2 x 2 x 2 x 2 = 32

 

Temos que descartar os 2 casos onde todas as barras são da mesma cor (todas pretas ou todas brancas).

 

Total: 30

Resposta: B

 

 

Questão 31. Um determinado setor do Poder Judiciário gasta R$ 3.600,00 com vale alimentação para 5 funcionários em 20 dias. Mantido o mesmo valor unitário do vale alimentação, o gasto do setor, em 150 dias e para 10 funcionários, será de

a) R$ 7.200,00

b) R$ 27.000,00

c) R$ 36.000,00

d) R$ 54.000,00

e) R$ 57.600,00

 

Resolução

Questão típica de regra de três composta.

R$            funcionários          dias

3600         5                            20

x               10                          150

↑               ↑                            ↑

 

3600/x = 5/10 . 20/150

3600/x = 1/2 . 2/15

3600/x = 1/15

x = 3600.15

x = 54000

 

Resposta: D

 

 

Questão 32. Se a soma de dois números é igual a 10 e o seu produto é igual a 20, a soma de seus quadrados é igual a

a) 30

b) 40

c) 50

d) 60

e) 80

 

Resolução

Sejam x e y esses números.

 

Temos:

x + y = 10

x.y = 20

 

Elevando todos os lados ao quadrado na primeira equação:

(x + y)² = 10²

x² + 2xy + y² = 100

 

Como xy = 20

x² + 2xy + y² = 100

x² + 2.20 + y² = 100

x² + 40 + y² = 100

x² + y² = 100 – 40

x² + y² = 60

 

Resposta: D

 

 

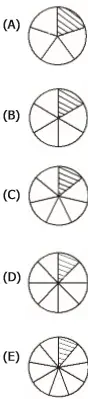
Questão 33. Se cada círculo desenhado abaixo está dividido em partes iguais entre si, assinale a alternativa que apresenta o círculo que tem 12,5% de sua área hachurada.

 

Resolução

A fração que corresponde a 12,5% é 1/8.

Como os círculos estão divididos em partes iguais, o desenho que corresponde a uma parte de oito é o da letra D.

 

Resposta: D

 

 

Questão 34. Se a área do desenho de um retângulo na escala 1:200 é de 50 cm², então a área real desse retângulo é de

a) 1 m²

b) 5 m²

c) 20 m²

d) 100 m²

e) 200 m²

 

Resolução

Se os lados do desenho são x e y, e a escala é 1:200, podemos concluir que os lados do retângulo são 200x e 200y.

 

Calculando a área:

200x.200y = 40000xy

 

Daí, temos que a área real é 40000 vezes maior do que a área do desenho:

50.40000 = 2.000.000 cm² = 200 m²

 

Resposta: E

 

 

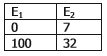
Questão 35. Para a conversão de escalas de E1 para E2 e vice-versa, utiliza-se a tabela abaixo.

Então, os valores x e y que completam corretamente a tabela abaixo

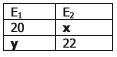
são, respectivamente,

a) 11 e 80

b) 12 e 60

c) 12 e 80

d) 14 e 60

e) 14 e 80

 

Resolução

Pela tabela 1 podemos observar que enquanto E1 cresce 100, E2 cresce 25, ou seja, E1 cresce 4 vezes mais rápido que E2.

A tabela 2 deve ter o mesmo padrão. Podemos observar que a única opção que mantém é a letra B:

E1: 20 – 60: crescimento de 40

E2: 12 – 22: crescimento de 10

 

Resposta: B

 

 

Questão 36. Cada técnico judiciário de um determinado setor do Tribunal de Justiça digitaliza 240 páginas de processo em uma jornada diária de 8 horas de trabalho. Se a jornada de trabalho em digitalização de cada técnico for reduzida para 5 horas diárias, a porcentagem mínima de contratação de novos servidores, para manter o mesmo nível de produtividade do setor, é de

a) 20%

b) 30%

c) 40%

d) 50%

e) 60%

 

Resolução

Vamos calcular quantas páginas um técnico consegue digitalizar em 5 horas diárias, e nas mesmas condições anteriores.

Páginas       h/d

240              8

x                  5

 

x/240 = 5/8

x = 240.5/8

x = 150 páginas

 

Veja que cada funcionário irá digitalizar 90 páginas a menos.

90 / 150 = 0,6 = 60%

Conclusão, para manter o nível de produtividade, é necessário contratar 60% a mais de funcionários.

 

Resposta: E

 

 

Questão 37. No Tribunal de Justiça, constatou-se a média semanal de ingresso de 20 processos na seção de Direito Criminal, 25 processos na seção de Direito Público e 35 processos na seção de Direito Privado. Em um montante de 560 processos a serem distribuídos entre as seções desse tribunal e de acordo com a média semanal constatada, as estimativas de número de processos para ingresso nas seções de Direito Criminal, Público e Privado são de, respectivamente,

a) 130, 175 e 255

b) 140, 165 e 255

c) 140, 175 e 245

d) 150, 165 e 245

e) 150, 175 e 235

 

Resolução

O primeiro passo é somar a média semanal de todos os processos:

20 + 25 + 35 = 80

 

Como existem 560 processos a serem distribuídos:

560 / 80 = 7

 

Veja que a quantidade de processos é 7 vezes superior à média semanal:

Direito Criminal: 20 x 7 = 140

Direito Público: 25 x 7 = 175

Direito Privado: 35 x 70 = 245

 

Resposta: C

 

 

Questão 38. A folha de papel A4 é, provavelmente, a mais utilizada em escritórios. Tem esse nome por ser resultante da quarta dobra sucessiva ao meio e pelo lado maior, da folha retangular A0, que tem área de 1 m² e lados na razão 1/√2.

Assim, a área de uma folha A4 é de

a) 1/32 m²

b) 1/16 m²

c) 1/8 m²

d) 1/2√2 m²

e) 1/√2 m²

 

Resolução

Quando dobramos uma folha ao meio, a área é reduzida pela metade, independente da medida dos lados. Assim, a área da folha A4, resultado da quarta dobra sucessiva de uma folha de área 1 m² é igual a 1/16 m².

 

Resposta: B

 

 

Questão 39. Os funcionários de um departamento do Tribunal de Justiça desejam comprar um forno de micro-ondas para uso comum do setor. O aparelho custa R$ 218,70. Para tanto, resolveram arrecadar dinheiro por meio de uma brincadeira: todos os dias úteis, o último funcionário a chegar ao setor deve colocar na “caixinha” o dobro da quantia que lá está em dinheiro. Para iniciar a brincadeira, o chefe do departamento colocou R$ 0,10 na “caixinha”. Contabilizando somente os dias úteis, o primeiro dia em que o forno de micro-ondas poderá ser comprado é o

a) 8

b) 12

c) 15

d) 30

e) 60

 

Resolução

Considerando que sempre haverá um funcionário chegando por último, o valor de R$ 0,10 dobrará a cada dia.

 

Primeiro dia

Depositado R$ 0,10

Acumulado R$ 0,10

 

Segundo dia

Depositado R$ 0,20

Acumulado R$ 0,30

 

Terceiro dia

Depositado R$ 0,60

Acumulado R$ 0,90

 

Quarto dia

Depositado R$ 1,80

Acumulado R$ 2,70

…

 

Temos uma PG, cujo primeiro termo é 0,1 e a razão é 3.

0,1 – 0,3 – 0,9 – 2,7 …

 

Utilizando a fórmula do termo geral da PG:

an = a1.q^n-1

218,7 = 0,1.3^n-1

3^n-1 = 218,7 / 0,1

3^n-1 = 2187

3^n-1 = 3⁷

n – 1 = 7

n = 8

 

Resposta: A

 

 

Questão 40. Os funcionários de um setor do Tribunal de Justiça estão organizando uma festa de despedida para um colega que irá se aposentar. Os valores recolhidos, por participante, são de R$ 50,00 para jovens ou adultos e de R$ 25,00 para crianças até 12 anos de idade. Sendo R$ 5.250,00 o valor total arrecadado e 120 o número de participantes, então os números de jovens ou adultos e de crianças que contribuíram para a festa são de, respectivamente,

a) 75 e 45

b) 80 e 40

c) 90 e 30

d) 100 e 20

e) 105 e 15

 

Resolução

Sejam x a quantidade de jovens ou adultos, e y a quantidade de crianças. Temos:

50x + 25y = 5250

x + y = 120

 

Organizando a segunda equação e substituindo na primeira:

x + y = 120

y = 120 – x

 

50x + 25y = 5250

50x + 25(120 – x) = 5250

50x + 3000 – 25x = 5250

25x = 5250 – 3000

25x = 2250

x = 90

 

x + y = 120

90 + y = 120

y = 120 – 90

y = 30

 

Resposta: C

 

 

Questão 41. Considere a figura abaixo.

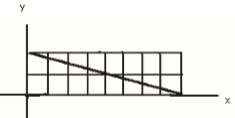
Assinale a alternativa que apresenta uma equação para a reta suporte do segmento oblíquo dessa figura.

a) x + 4y – 8 = 0

b) 4y – x – 8 = 0

c) x + 2y – 8 = 0

d) x + 4y + 8 = 0

e) 4y – x + 8 = 0

 

Resolução

Vamos descobrir a equação da reta representada utilizando os conceitos de equação reduzida.

y = mx + n, onde m é o coeficiente angular e n é o coeficiente linear.

 

Como a reta corta o eixo y no ponto (0, 2), n = 2.

 

Pela figura, é possível observar que enquanto x passa de 0 a 8, y decresce de 2 a 0. Assim, temos que:

m = (y₂ – y₁) / (x₂ – x₁)

m = (0 – 2) / (8 – 0)

m = -2/8

m = -1/4

 

Substituindo na equação reduzida:

y = mx + n

y = (-1/4)x + 2

4y = -x + 8

x + 4y – 8 = 0

 

Resposta: A

 

 

Questão 42. Um desenhista do Tribunal de Justiça quer traçar um retângulo com perímetro de 28 cm e com a maior área possível. O valor dessa área será de

a) 14 cm²

b) 21 cm²

c) 49 cm²

d) 56 cm²

e) 70 cm²

 

Resolução

Tratando-se de um retângulo, e como o perímetro é igual a 28, se um dos lados mede x, o outro medirá 14 – x, e a função da área em função do lado x será:

A(x) = x.(14 – x)

A(x) = -x² + 14x

 

Temos uma função quadrática, que possui valor máximo, já que a<0.

Pela forma como foi construída, podemos perceber que as raízes da função são 0 e 14, de onde concluímos que o x do vértice é 7.

 

Calculando o y do vértice

A(x) = -x² + 14x

A(7) = -7² + 14.7

A(7) = -49 + 98

A(7) = 49 cm²

 

Resposta: C

 

 

Questão 43. A calçada em frente ao prédio do Tribunal de Justiça será reformada, colocando-se lajotas retangulares e quadrangulares de mesma área. Se um dos lados da lajota retangular mede 40 cm e o outro lado mede 30 cm a mais que o lado da lajota quadrangular, então as medidas das lajotas retangular e quadrangular são, respectivamente,

a) 0,4m x 0,6m e 0,9m x 0,9m

b) 0,9dm x 0,4dm e 0,6dm x 0,6dm

c) 0,9m x 0,6m e 0,4m x 0,4m

d) 0,9m x 0,4m e 0,6m x 0,6m

e) 90dm x 40dm e 60dm x 60dm

 

Resolução

Considerando que os lados das lajotas quadrangulares medem x cm, os lados das lajotas retangulares medirão 40 cm e x + 30 cm.

 

Área do quadrangular

x²

 

Área do retangular

40.(x + 30) = 40x + 1200

 

Como as áreas são iguais:

x² = 40x + 1200

x² – 40x – 1200 = 0

 

Resolvendo a equação do segundo grau

∆ = b² – 4ac

∆ = (-40)² – 4.1.(-1200)

∆ = 1600 + 4800

∆ = 6400

 

x = (-b +- √∆)/2a

x = (40 +- √6400)/2.1

x = (40 +- 80)/2

 

Como x representa a medida de um lado, vamos considerar apenas a raiz positiva:

x = (40 + 80)/2

x = 120/2

x = 60 cm

 

Assim, as medidas dos lados serão:

lajota quadrangular: 60 cm x 60 cm

lajota retangular: 40 cm x 90 cm

 

Convertendo para metros

lajota quadrangular: 0,6 m x 0,6 m

lajota retangular: 0,4 m x 0,9 m

 

Resposta: D

 

 

Questão 44. A base CB do retângulo ABCD é dividida em 4 partes de mesma medida pelos pontos M, N e O. O ponto P está sobre o lado AB. A razão entre a área do retângulo ABCD e a área do triângulo MPO é

a) 2

b) 3

c) 4

d) 6

e) 8

 

 

Questão 45. Os desenhistas do Tribunal de Justiça estão projetando um jardim com quadrados de 2 m de lado contendo canteiros triangulares com área destinada ao plantio de flores da estação e áreas com pedras d’água. A figura abaixo representa um desses quadrados, onde M e N são os pontos médios dos lados AB e BC, respectivamente.

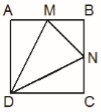
Se as flores forem plantadas no triângulo DMN, elas ocuparão uma área de

a) 1,5 m²

b) 2 m²

c) 2,5 m²

d) 3,5 m²

e) 4 m²

 

Resolução

O caminho mais fácil é calcular a área dos demais triângulos e subtrair da área do quadrado.

 

Área do quadrado:

2² = 4 m²

 

A área dos demais triângulos:

Área de DCN

b.h/2 = 2.1/2 = 1 m²

Área de MAD

b.h/2 = 1.2/2 = 1 m²

Área de MBN

b.h/2 = 1.1/2 = 0,5 m²

 

Área total dos três triângulos:

1 + 1 + 0,5 = 2,5 m²

 

Área do triângulo MND:

4 – 2,5 = 1,5 m²

 

Resposta: A

 

 

Questão 46. Em um prédio do Tribunal de Justiça, há um desnível de altura entre a calçada frontal e a sua porta de entrada. Deseja-se substituir a escada de acesso existente por uma rampa. Se a escada possui 40 degraus iguais, cada um com altura de 12,5 cm e comprimento de 30 cm, o comprimento da rampa será de

a) 5 m

b) 8 m

c) 10 m

d) 12 m

e) 13 m

 

Existem 40 degraus com 12,5 cm de altura e 30 cm de comprimento.

 

A altura total da escada é de:

40 x 12,5 = 500 cm = 5 m

 

O comprimento total da escada é de:

40 x 30 = 1200 cm = 12 m

 

 

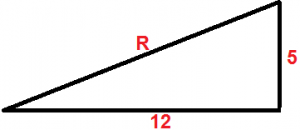
Veja que temos um triângulo retângulo, onde chamaremos de R o comprimento da rampa.

Utilizando o Teorema de Pitágoras:

R² = 12² + 5²

R² = 144 + 25

R² = 169

R = 13 m

 

Resposta: E

 

 

Gostou da prova resolvida do TJ RS 2012?

Deixe o seu comentário.