Estudando matemática para concursos? Confira a prova resolvida do concurso para o TJ do PR, realizado em 2014 pela UFPR.
Questão 21 – Uma caixa contém certa quantidade de lâmpadas. Ao retirá-las de 3 em 3 ou de 5 em 5, sobram 2 lâmpadas na caixa. Entretanto, se as lâmpadas forem removidas de 7 em 7, sobrará uma única lâmpada. Assinale a alternativa correspondente à quantidade de lâmpadas que há na caixa, sabendo que esta comporta um máximo de 100 lâmpadas.
a) 36.
b) 57.
c) 78.
d) 92.
Vamos resolver por eliminação:
Podemos descartar o 36, o 57 e o 78 pois são múltiplos de 3, por este motivo, não sobrariam duas lâmpadas.
Basta então verificar que:
92 = 3.30 + 2
92 = 5.18 + 2
92 = 7.13 + 1
Questão 22 – Devido a um acidente ocorrido em alto mar, uma grande quantidade de óleo está vazando de um navio cargueiro.
Suponha que a mancha de óleo gerada por esse vazamento esteja se espalhando uniformemente em todas as direções e que, após algumas horas do início do vazamento, estima-se que a mancha terá assumido o formato circular, com raio de 500 metros. Qual será a área coberta pelo óleo nesse momento? (Use pi = 3,14)
a) 0,157 km²
b) 0,471 km²
c) 0,785 km²
d) 1,57 km²
Como as respostas estão em km, vamos considerar 500m = 0,5km
Pela fórmula de área de uma circunferência:
A = pi.r² = 3,14.0,5² = 3,15.0,25 = 0,785km²
Questão 23 – Após viajar 300 km e chegar ao seu destino, um motorista percebeu que, se sua velocidade média na viagem tivesse sido 10 km/h superior, ele teria diminuído o tempo da viagem em 1 hora. Quanto tempo o motorista gastou na viagem?
a) 6 horas.
b) 5,5 horas.
c) 5 horas.
d) 4,5 horas.
Temos que velocidade é igual a distância sobre o tempo.
Sendo v a velocidade e t o tempo, temos duas equações:
(1) v = 300/t
(2) v + 10 = 300/(t – 1)
Substituindo (1) em (2):
300/t + 10 = 300/(t – 1)
(300 + 10t)/t = 300/(t – 1)
300t = (300 + 10t).(t – 1)
300t = 300t – 300 + 10t² – 10t
10t² – 10t – 300 = 0
t² – t – 30 = 0
Resolvendo pelo método da soma e produto:
Soma = -b/a = -(-1)/1 = 1
Produto = c/a = (-30)/1 = -30
Os dois números cuja soma é 1 e o produto é -30 são -5 e 6.
Descartando a solução negativa, a resposta é 6 horas.
Questão 24 – Abaixo estão representados os primeiros passos da construção de uma sequência de figuras formadas por quadrados. Nessa sequência, cada figura é obtida a partir da figura anterior seguindo-se certa regra, conforme indicado a seguir:
Seguindo essa mesma regra, quantos quadrados terá a figura do passo 20?
a) 125 quadrados.
b) 421 quadrados.
c) 653 quadrados.
d) 761 quadrados
Analisando as figuras, temos que a quantidade de quadrinhos da figura 20 pode ser calculada como:
1 + 4 + 8 + 12 + 16 + …
A quantidade será a soma da PA que começa com 4, a razão é 4 e tem 19 elementos, mais 1.
Primeiramente vamos calcular o 19º termo dessa PA, utilizando a fórmula do termo geral:
an = a1 + (n-1)r
a19 = 4 + (19-1).4 = 4 + 18.4 = 76
Vamos agora somar a PA utilizando a fórmula da soma:
S = (a1 + an).n/2
S = (4 + 76).19/2 = 80.19/2 = 40.19 = 760
A quantidade total será então 760 + 1 = 761
Questão 25 – Um grupo de alunos deseja comprar um livro como presente para sua professora. Se cada aluno contribuir com R$ 9,00 para a compra do livro, haverá R$ 11,00 de troco ao final. Por outro lado, se cada aluno contribuir com R$ 6,00, faltarão
R$ 16,00 para completar o valor do livro. Qual é o preço do livro?
a) R$ 56,00.
b) R$ 64,00.
c) R$ 70,00.
d) R$ 85,00.
Sejam x a quantidade de alunos e y o preço do livro. Temos duas equações:
(1) 9x = y + 11
(2) 6x = y – 16
Fazendo (1) – (2):
9x – 6x = y + 11 – y + 16
3x = 27
x = 27/3 = 9
Vamos substituir o valor encontrado em (1) para acharmos o valor de y:
9.9 = y + 11
81 = y + 11
y = 81 – 11
y = 70
Questão 26 – Um tanque é abastecido com água por três torneiras, cada uma com uma vazão diferente, que podem ser abertas e
fechadas individualmente. Quando o tanque se encontra vazio, cada uma delas é capaz de enchê-lo em 2, 5 e 10 horas
individualmente. Se as três torneiras forem abertas simultaneamente, no momento em que o tanque está vazio, quanto
tempo será necessário para enchê-lo?
a) 1 hora e 15 minutos.
b) 1 hora e 48 minutos.
c) 3 horas e 20 minutos.
d) 7 horas e 12 minutos.
Sendo x o tempo total, considerando que 2, 5 e 10 são inversamente proporcionais a vazão das torneiras, e que 1 representa o tanque cheio, temos a seguinte equação:
x/2 + x/5 + x/10 = 1
(5x + 2x + x)/10 = 1
8x/10 =1
x = 10/8 = 1,25
Convertendo para horas, 1,25 corresponde a 1 hora e 15 minutos
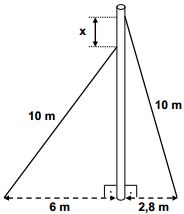
Questão 27 – Um mastro é mantido na vertical por meio de dois cabos de 10 m de comprimento. O primeiro está fixado a 6 m da base do mastro, e o segundo a 2,8 m da base, conforme indica a figura. Determine a distância x entre as alturas dos pontos de fixação dos cabos no mastro.
a) 1,2 m.
b) 1,6 m.
c) 2,4 m.
d) 2,8 m.
Temos que utilizar o Teorema de Pitágoras nos dois triângulos:
Triângulo da esquerda:
10² = 6² + h²
100 – 36 = h²
h² = 64
h = 8
Triângulo da direita:
10² = 2,8² + H²
100 – 7,84 = H²
H² = 92.16
H = 9,6
Daí, x = H – h = 9,6 – 8 = 1,6m
Questão 28 – Após o processo de recuperação de uma reserva ambiental, uma espécie de aves, que havia sido extinta nessa reserva, foi reintroduzida. Os biólogos responsáveis por essa área estimam que o número P de aves dessa espécie, t anos após
ser reintroduzida na reserva, possa ser calculado pela expressão
De acordo com essa estimativa, quantos anos serão necessários para dobrar a população inicialmente reintroduzida?
a) 2 anos.
b) 4 anos.
c) 8 anos.
d) 16 anos.
Queremos que a população dobre.
Para sabermos quantas aves existiam no início, basta tomar t = 0:
P = 300 / (7 + 8.0,5) = 300 / (7 + 4) = 300 / 15 = 20 aves
Precisamos então que a população chegue a 40 aves:
40 = 300 / (7 + 8.(0,5)^t)
7 + 8.(0,5)^t = 300/40
7 + 8.(0,5)^t = 7,5
8.(0,5)^t = 7,5 – 7
8.(0,5)^t = 0,5
(0,5)^t = 0,5 / 8
(0,5)^t = 0,0625
t = 4
Questão 29 – Suponha que o tempo necessário para se tomar uma decisão esteja relacionado com o número de escolhas de que se dispõe. Nesse caso, um modelo matemático que fornece o tempo de reação R, em segundos, em função do número de escolhas N, é dado pela expressão:
R = 0,17 + 0,44 log(N)
De acordo com esse modelo, quando o número de escolhas for reduzido de 100 para 10, qual será o percentual de diminuição no tempo de reação, aproximadamente?
a) 26%.
b) 42%.
c) 55%.
d) 88%.
Quando N = 100:
R = 0,17 + 0,44.log100 = 0,17 + 0,44.2 = 0,17 + 0,88 = 1,05
Quando N = 10:
R = 0,17 + 0,44.log10 = 0,17 + 0,44.1 = 0,17 + 0,44 = 0,61
Nota-se que a queda foi de 1,05 – 0,61 = 0,44
Calculando a queda percentual:
0,44/1,05 = 0,419 = 42%
Questão 30 – Um investimento rende juros compostos a uma taxa de 6% ao ano. Depois de quantos anos, um valor inicial de
R$ 1.000,00 chegará ao valor de R$ 10.000,00 com esse investimento? (Use log(1,06) = 0,025)
a) 20 anos.
b) 30 anos.
c) 40 anos.
d) 50 anos.
Pela fórmula de juros compostos:
M = C x (1 + i)^n
10.000 = 1.000 x (1 + 0,06)^n
10 = 1,06^n
n x log1,06 = log10
n x 0,025 = 1
n = 1/0,025
n = 40 anos