Confira aqui a prova de Raciocínio Lógico‐quantitativo para o cargo de Assistente Técnico Judiciário do Tribunal de Justiça do Amazonas (TJ AM), aplicada em 2013 pela FGV (Fundação Getúlio Vargas).
Boa sorte!
Questão 16. Dona Maria tem quatro filhos: Francisco, Paulo, Raimundo e Sebastião. A esse respeito, sabe‐se que
I. Sebastião é mais velho que Raimundo.
II. Francisco é mais novo que Paulo.
III. Paulo é mais velho que Raimundo.
Assim, é obrigatoriamente verdadeiro que
(A) Paulo é o mais velho.
(B) Raimundo é o mais novo.
(C) Francisco é o mais novo.
(D) Raimundo não é o mais novo.
(E) Sebastião não é o mais novo.
Resolução
Analisando as afirmações, temos:
I. S>R (Saulo é mais velho que Raimundo)
II. P>F (Paulo é mais velho que Francisco)
III. P>R (Paulo é mais velho que Raimundo)
Podemos descartar a letra A e a letra C porque os filhos podem ser organizados da seguinte forma:
S>P>F>R
Podemos descartar a letra B e a letra D porque os filhos podem ser organizados da seguinte forma:
S>P>R>F
A letra E é obrigatoriamente verdadeira pela afirmação I.
Resposta: E
Questão 17. Ana deseja formar uma senha de cinco caracteres usando as três letras de seu nome e os dois algarismos da dezena do ano de seu nascimento, 1994. Ela decidiu que manterá a ordem das letras de seu nome, ANA, bem como a ordem dos dois algarismos, 94, mas não manterá, necessariamente, as três letras juntas e os dois algarismos juntos. Além disso, decidiu que a senha começará por uma letra. Assim, por exemplo, AN94A é uma possível senha para Ana.
Assinale a alternativa que indica a quantidade de escolhas que Ana tem para a sua senha, de acordo com os critérios que ela estabeleceu.
(A) 6
(B) 7
(C) 8
(D) 9
(E) 10
Resolução
Não podemos alterar as ordens das letras ou dos números.
Outra informação valiosa é que a senha deve começar por uma letra, ou seja, pela letra A.
Como a senha apresenta poucos caracteres, podemos listar todas as opções apenas nos concentrando nos números 9 e 4.
A94NA
A9N4A
A9NA4
AN94A
AN9A4
ANA94
A questão também pode ser resolvida através das ferramentas de análise combinatória:
Devemos distribuir os caracteres 9, 4, N e A nas posições 2 a 5.
P(4) = 4.3.2.1 = 24
Descartando as opções em que o 4 vem antes do 9 (metade):
24 / 2 = 12
Descartando as opções em que o A vem antes do N (metade):
12 / 2 = 6
Resposta: A
Questão 18. Considere como verdadeiras as sentenças a seguir.
I. Alguns matemáticos são professores.
II. Nenhum físico é matemático.
Então, é necessariamente verdade que
(A) algum professor é físico.
(B) nenhum professor é físico.
(C) algum físico é professor.
(D) algum professor não é físico.
(E) nenhum físico é professor.
Resolução
Podemos afirmar que os professores que são matemáticos NÃO são físicos, basta observar que nenhum físico é matemático. Assim, alguns professores (aqueles que são matemáticos) não são
físicos.
Resposta: D
Questão 19. Se não é verdade que “Todos assistentes judiciários de determinado fórum são formados em advocacia”, então é necessariamente verdade que
(A) nenhum assistente judiciário desse fórum é formado em advocacia.
(B) todos assistentes judiciários desse fórum não são formados em advocacia.
(C) ninguém formado em advocacia é assistente judiciário desse fórum.
(D) alguém formado em advocacia é assistente judiciário desse fórum.
(E) algum assistente judiciário desse fórum não é formado em advocacia.
Resolução
Para negarmos a proposição iniciada por Todos, basta dizermos que “ALGUM assistente judiciário NÃO é formado em advocacia”.
Resposta: E
Questão 20. Em um determinado fórum, dezessete processos foram analisados em uma semana, de 2a feira a 6a feira. Assim, é necessariamente verdade que
(A) em algum dia da semana foram analisados quatro ou mais processos.
(B) em cada dia da semana foi analisado pelo menos um processo.
(C) em cada dia da semana foram analisados pelo menos dois processos.
(D) em nenhum dia da semana foram analisados mais de dez processos.
(E) em algum dia da semana não foi analisado processo algum.
Resolução
Questão envolvendo o Princípio da Casa dos Pombos.
15 processos / 5 dias = 3 processos
Como são 17, os dois restantes nos deixam afirmar que “em algum dia da semana foram analisados quatro processos ou mais” (letra A).
Resposta: A
Questão 21. Considere que, para se deslocar no espaço bidimensional, uma partícula só possa fazer movimentos nos sentidos norte (N), sul (S), leste (L), oeste (O) e que, cada deslocamento corresponda a uma unidade de comprimento.
Suponha que, partindo de um ponto A, uma partícula tenha se deslocado até um ponto B percorrendo a trajetória N N L N L L N N O S O N.
Outra trajetória que essa partícula poderia percorrer para se deslocar do ponto A até o ponto B é
(A) L L S S N N N N N N O
(B) S L N L S S O O S O S S
(C) N N L N N L N N L S O
(D) N L L N N N N O
(E) L L N N N N N L
Resolução
A ordem não importa. Perceba que se as trajetórias N L e L N levam a partícula ao mesmo lugar.
Outra observação importante é que os opostos se anulam, por exemplo, a trajetória N S não leva a partícula a lugar algum.
Analisando a trajetória, temos:
6N, 3L, 2O e 1S
Como os opostos se anulam, podemos eliminar um deslocamento em cada direção:
5N, 2L, 1O
Sabendo que a ordem é irrelevante, a opção correta é a letra D, pois contem 5N, 2L e 1O.
Resposta: D
Questão 22. Abel, Bruno, Carlos, Diogo, Elias e Fernando estão, respectivamente, sobre os vértices A, B, C, D, E e F de um hexágono regular, dispostos nessa ordem e no sentido horário.
Sejam a, b, c, d e e as distâncias de Fernando, respectivamente, a Abel, Bruno, Carlos, Diogo e Elias, então é correto afirmar que
(A) a = b = c = d =e
(B) a < b < c < d < e = 2a
(C) a = e < b= d < c = 2a
(D) a = b < d= e < c = 2a
(E) a = c < b= d < e = 2a
Resolução
Observe nas figuras abaixo que Fernando está localizado no vértice F, sendo a, b, c, d e e as distâncias até Abel, Bruno, Carlos, Diogo e Elias, respectivamente.
No primeiro hexágono é possível observar que a=e e b=d, e também que a<b<c.
No segundo, considerando que um hexágono regular pode ser dividido em 6 triângulos equiláteros, podemos concluir que c = 2a.
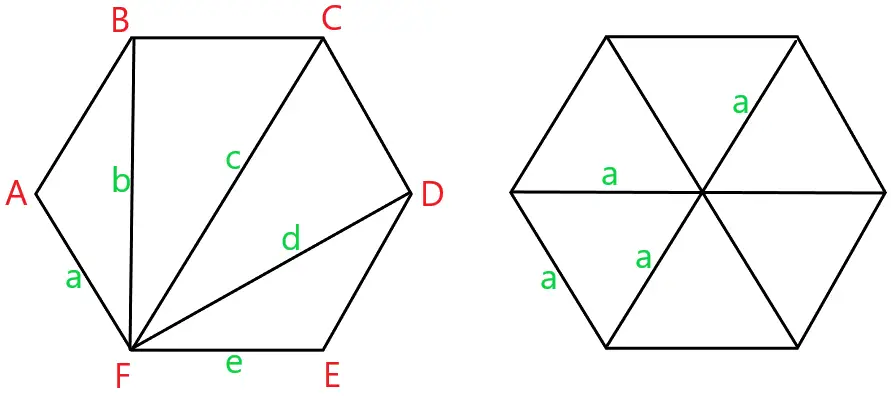
Daí, a = e < b = d < c = 2a.
Resposta: C
Questão 23. Considere como verdadeiras as sentenças a seguir.
I. Se André não é americano, então Bruno é francês.
II. Se André é americano então Carlos não é inglês.
III. Se Bruno não é francês então Carlos é inglês.
Logo, tem‐se obrigatoriamente que
(A) Bruno é francês.
(B) André é americano.
(C) Bruno não é francês.
(D) Carlos é inglês.
(E) André não é americano.
Resolução
André é americano ou não é americano. Analisando I e II, podemos concluir que:
“ou Bruno é francês ou Carlos não é inglês”
Analisando a afirmação III, a equivalente é:
“Se Carlos não é inglês, então Bruno é francês”
Veja que se Carlos não é inglês, teremos que Bruno é francês, contrariando a disjunção exclusiva.
Daí, podemos concluir que Bruno é francês.
Resposta: A
Questão 24. A respeito de um conjunto de cem processos judiciais, sabe‐se que
I. pelo menos um deles é de 2o grau;
II. entre quaisquer quatro desses processos, pelo menos um é de 1o grau.
Sobre esse conjunto de processos judiciais tem‐se que
(A) exatamente setenta e cinco são de 1o grau.
(B) no máximo noventa e sete são de 2o grau.
(C) no mínimo noventa e sete são de 1o grau.
(D) no máximo vinte e cinco são de 2o grau.
(E) no máximo setenta e cinco são de 1o grau.
Resolução
Por II, escolhendo 4 processos ao acaso, pelo menos um deles é de 1o grau, ou seja, na pior das hipóteses, existem 3 processos de 1o grau, e todos foram escolhidos.
Como são 100 processos, e, no máximo, 3 não são de 1o grau, podemos concluir que no mínimo 97 processos não são de 1o grau.
Resposta: C
Questão 25. Em um fórum há 60 processos judiciais, sendo que o menor tem 30 páginas e o maior tem 42 páginas.
Considere que cada processo tenha um número inteiro de páginas. Sobre esses 60 processos judiciais, é obrigatoriamente verdadeiro que
(A) o total de páginas é maior que 2400.
(B) cada processo tem, em média, 36 páginas.
(C) nenhum processo tem exata mente 36 páginas.
(D) pelo menos um processo tem exatamente 36 páginas.
(E) há pelo menos cinco processos com exatamente o mesmo número de páginas.
Resolução
A e B são afirmações falsas.
Poderíamos ter 59 processos com 30 páginas e 1 com 42 páginas.
C e D são afirmações falsas.
Com as informações da questão, não podemos afirmar que existe processo com ou sem 36 páginas, exatamente.
Considerando que a quantidade de páginas está limitada entre 30 e 42 páginas, temos 13 opções para cada processo.
Como 13 x 4 = 52, na pior das hipóteses, teremos 4 processos com cada uma das 13 opções de páginas, totalizando 52 processos:
4 processos com 30 páginas
4 processos com 31 páginas
4 processos com 32 páginas
…
4 processos com 42 páginas
O 53o obrigatoriamente estará em um desses grupos, ou seja, pelo menos 5 processos terão exatamente a mesma quantidade de páginas.
Resposta: E
Gostou da resolução da prova de assistente técnico judiciário do TJ AM 2013?
Deixe o seu comentário.
