Confira aqui a prova resolvida do concurso para a PRF, realizado em 2021 pelo CESPE.
O gabarito oficial está previsto para ser divulgado amanhã.
Gabarito extraoficial de matemática e raciocínio lógico.
Boa sorte a todos!!!!
Foi modelado que o espalhamento de uma notícia em uma população – entendido como o percentual de indivíduos dessa população que recebe essa notícia por unidade de tempo – é diretamente proporcional ao percentual de indivíduos da população que já conhecem a notícia multiplicado pelo percentual de indivíduos dessa população que ainda não a conhecem até aquele instante. A constante k de proporcionalidade depende, entre outros fatores, do impacto da notícia na vida dos envolvidos e de propriedades dos meios de comunicação disponíveis.
Tendo como base essas informações e considerando que, para certa notícia, k = 1, julgue os itens seguintes.
Comentário:
A questão informa que o espalhamento de uma notícia E(x) é diretamente proporcional ao percentual de indivíduos da população que já conhecem a notícia multiplicado pelo percentual de indivíduos dessa população que ainda não a conhecem até aquele instante.
Considerando que x é o percentual de indivíduos que já conhecem a notícia até aquele instante, temos que:
E(x) = x . (1 – x) . k, onde k é a constante de proporcionalidade.
Como devemos considerar k = 1, temos:
E(x) = x . (1 – x)
Questão 27. Se, em determinado instante, o espalhamento de uma notícia é igual a 16% por unidade de tempo, então, nesse instante, mais de 75% da população ainda desconhece a notícia.
Resolução
E(x) = x . (1 – x)
0,16 = x – x²
-x² + x – 0,16 = 0
Resolvendo a equação do segundo grau:
Δ = b² – 4ac
Δ = 1² – 4.(-1).(-0,16)
Δ = 1 – 0,64
Δ = 0,36
x = (- b +- √Δ ) / 2a
x = (- 1 +- √0,36 ) / 2(-1)
x = (- 1 +- 0,6 ) / (-2)
x’ = (- 1 + 0,6 ) / (-2) = 0,2 = 20%
x’’ = (- 1 – 0,6 ) / (-2) = 0,8 = 80%
Veja que quando o espelhamento é de 16%, x = 20% ou x = 80%. De onde concluímos que 20% da população desconhece a doença ou 80% da população desconhece a doença.
Isto acontece porque o gráfico da função espelhamento é uma função do segundo grau, com cavidade para baixo.
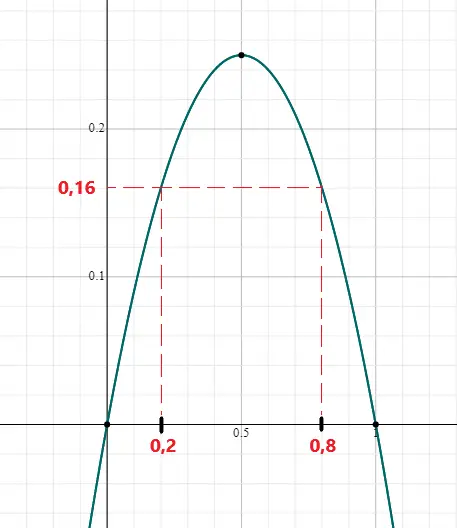
Como x = 20% é um valor válido para o espelhamento de 80%, podemos concluir que a afirmação está INCORRETA.
Questão 28. O espalhamento de uma notícia será tanto maior quanto maior for o número de pessoas que dela tiverem tomado conhecimento.
Resolução
Como foi visto no item anterior, a função espelhamento E(x) é uma função do segundo grau, com cavidade para baixo, ou seja, essa afirmação é verdadeira apenas até o x do vértice, pois após este ponto, o percentual de quem conhece a notícia continua aumentando, porém o espelhamento começa a cair.
Resposta: ERRADO.
Questão 29. Se, em determinado instante, 30% da população já conhece a notícia, então, nesse instante, o seu espalhamento estaria em patamar superior a 20% por unidade tempo.
Resolução
E(x) = x . (1 – x)
E(0,3) = 0,3 . 0,7
E(0,3) = 0,21 = 21%
Resposta: CERTO
Questão 30. De acordo com a modelagem realizada, é possível que, em determinado instante, o espalhamento da notícia seja superior a 50% por unidade de tempo.
Resolução
Considerando que o gráfico é uma parábola com cavidade para baixo, ele tem um ponto máximo, que é o x do vértice.
E(x) = x . (1 – x)
E(x) = x – x²
xv = -b / 2a = -1/2(-1) = 1/2 = 0,5 = 50%
Calculando E(0,5):
E(x) = x – x²
E(0,5) = 0,5 – 0,5²
E(0,5) = 0,5 – 0,25
E(0,5) = 0,25 = 25%.
O espelhamento máximo é de 25%.
Resposta: ERRADO
Em uma operação da PRF, foram fiscalizados: 20 veículos automotores até o fim da primeira hora; 60 veículos automotores até o fim da segunda hora; 120 veículos automotores até o fim da terceira hora; 200 veículos automotores até o fim da quarta hora e 300 veículos automotores até o fim da quinta hora. O padrão numérico observado manteve-se até o fim da décima hora, quando, então, foi finalizada a operação.
Considerando essa situação hipotética, julgue os itens seguintes.
Questão 31. Mais de 550 veículos terão sido fiscalizados até o fim da sétima hora de realização da operação.
Resolução
Hora 1: 20 veículos
Hora 2: 60 veículos
Hora 3: 120 veículos
Hora 4: 200 veículos
Hora 5: 300 veículos
…
Diferença:
H2 – H1 = 60 – 20 = 40
H3 – H2 = 120 – 60 = 60
H4 – H3 = 200 – 120 = 80
H5 – H4 = 300 – 200 = 100
Observe que os aumentos têm um acréscimo de 20 veículos a cada hora, ou seja, os próximos aumentos serão de 120 e 140.
Hora 6: 300 + 120 = 420
Hora 7: 420 + 140 = 560
Resposta: CORRETO
Questão 32. Considere que {qn}, n variando de 1 a 10, seja a sequência numérica formada pelas quantidades de veículos fiscalizados apenas no decorrer da n-ésima hora de realização da operação, ou seja, q1 é a quantidade de veículos fiscalizados apenas no decorrer da primeira hora de realização da operação; q2 é a quantidade de veículos fiscalizados apenas no decorrer da segunda hora de realização da operação; e assim por diante. Nessa situação, a sequência {qn}, para n variando de 1 a 10, é uma progressão aritmética.
Resolução
Veículos fiscalizados na primeira hora (q1): 20
Veículos fiscalizados na segunda hora (q2): 40
Veículos fiscalizados na terceira hora (q3): 60
Veículos fiscalizados na quarta hora (q4): 80
Veículos fiscalizados na quinta hora (q5): 100
Veículos fiscalizados na sexta hora (q6): 120
Observe que a quantidade de veículos fiscalizados aumenta em 20 veículos por hora. Temos aqui uma progressão aritmética de razão 20.
Resposta: CERTO
Veja no YouTube:
Gostou da resolução da prova da PRF 2021?
Deixe o seu comentário.
