Confira aqui a prova resolvida do concurso para professor de matemática da educação básica da Prefeitura de Teresina – Piauí, organizado em 2019 pela NUCEPE.

Bom estudo!

Questão 1. A figura a seguir é formada por quatro triângulos unidos pelos vértices nos quais estão em destaque, na cor cinza, alguns ângulos internos.

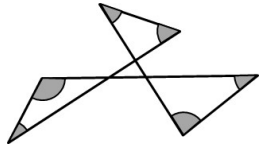
Qual a soma dos ângulos internos em destaque?

a) 180º.

b) 270º.

c) 360º.

d) 540º.

e) 720º.

Resolução

Observe na figura abaixo que os ângulos com a mesma cor são opostos pelo vértice, e por consequência, são congruentes.

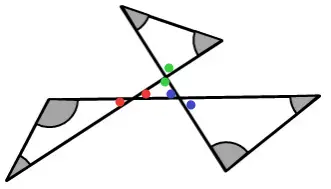
A soma dos ângulos internos de um triângulo é igual a 180°, ou seja, a soma dos ângulos internos dos três maiores triângulos é igual a:

3 x 180° = 540°

Podemos calcular a soma dos ângulos internos em destaque subtraindo a soma dos ângulos coloridos de 540°.

Observe no triângulo do meio que a soma dos ângulos coloridos é igual a 180°, ou seja, podemos calcular a soma buscada pela questão através da subtração:

540º – 180º = 360º

Resposta: C

Questão 2. Paulo escreveu dois números naturais em seu caderno, cada um deles com quatro algarismos diferentes. O maior deles só tem algarismos ímpares e o menor só tem algarismos pares. Sabendo que a diferença entre o maior número e o menor é a maior possível, qual é esta diferença?

a) 1 111.

b) 7 285.

c) 7 293.

d) 7 707.

e) 9 507.

Resolução

A diferença entre os números naturais escrito por Paulo deve ser a maior possível, ou seja, o maior deles deve ser o maior possível, e o menor deles deve ser o menor possível, dentro das características informadas pela questão.

O maior possui quatro algarismos diferentes, todos ímpares, ou seja, trata-se do número 9753.

O menor possui quatro algarismos diferentes, todos pares, ou seja, trata-se do número 2046.

Calculando a diferença:

9753 – 2046 = 7707

Resposta: D

Questão 3. Lívia quer pintar as quatro paredes de seu quarto de modo que paredes adjacentes tenham cores distintas. Ela dispõe de cinco tipos de cores. De quantas maneiras diferentes Lívia pode pintar seu quarto?

a) 80.

b) 120.

c) 180.

d) 240.

e) 260.

Resolução

A Lívia deve escolher um lado para começar a pintar, e depois seguir a ordem da esquerda para a direita, ou vice-versa.

O primeiro lado a ser pintado possui 5 opções de cores.

O segundo lado possui 4 opções, pois é adjacente ao lado anterior e não pode ser da mesma cor.

A partir do terceiro, temos dois casos a considerar:

Caso 1 (o terceiro lado possui a mesma cor do primeiro)

Neste caso, temos uma opção para o terceiro lado, e como os lados 1 e 3 são da mesma cor, temos 4 opções para o quarto lado.

5 x 4 x 1 x 4 = 80

Caso 2 (o terceiro lado possui cor diferente do primeiro)

Neste caso, temos 3 opções para o terceiro lado, que deve ser diferente do primeiro e do segundo.

O quarto lado deve ser diferente do primeiro e do terceiro, por ser adjacente a eles.

5 x 4 x 3 x 3 = 180

Total de possibilidades:

80 + 180 = 260

Resposta: E

Questão 4. Na divisão de dois números naturais, o quociente é 21 e o resto é o maior possível. Se a diferença do dividendo pelo o divisor é 251, qual é o resto dessa divisão?

a) 8.

b) 9.

c) 10.

d) 11.

e) 12.

Considere:

D = dividendo

d = divisor

R = resto

Como R deve ser o maior possível, podemos concluir que R = d-1.

21d + R = D

21d + (d – 1) = D

22d -1 = D

Como D – d = 251, D = 251 + d.

22d – 1 = 251 + d

22d – d = 251 + 1

20d = 252

d = 252/21

d = 12

R = d – 1

R = 12 – 1

R = 11

Resposta: D

Questão 5. Paulo consultou um médico e foi receitado com três tipos de remédios, para um tratamento de 60 dias
completos. O remédio A deverá ser tomado a cada 4 horas, o B a cada 6 horas e o C a cada 10 horas. Paulo
iniciou o tratamento tomando os remédios A, B e C no mesmo horário. Supondo que ele tomará, rigorosamente, toda medicação no horário da ingestão dos medicamentos, então o número de vezes em que os três remédios serão ingeridos simultaneamente será:

a) 12 vezes.

b) 24 vezes.

c) 25 vezes.

d) 30 vezes.

e) 120 vezes.

Resolução

Inicialmente, devemos calcular a quantidade de horas em 60 dias:

60 x 24 = 1440 horas

Os remédios serão tomados a cada 4, 6 e 10 horas, e a questão deseja saber a quantidade de vezes que serão ingeridos ao mesmo simultaneamente. Temos aqui o conceito de MMC.

MMC(4,6,10) = 60

Dividindo 1440 por 60:

1440 / 60 = 24

Devemos apenas considerar o início do tratamento, quando Paulo tomou todos os remédios:

24 + 1 = 25

Resposta: C

Questão 6. Um ferreiro vai confeccionar pedaços de barras de ferro de mesma medida. Ele dispõe de 35 barras de
270 cm, 18 de 540 cm e 6 de 810 cm, todas de igual largura. Ele pretende cortar as barras em pedaços de
mesmo comprimento, sem deixar sobras, de modo que esses pedaços fiquem o maior possível, mas de
comprimento menor que 1 m. Quantas pedaços de barra de ferro o ferreiro pode produzir?

a) 89.

b) 178.

c) 267.

d) 524.

e) 801.

Resolução

Precisamos dividir as barras de 270, 540 e 810 cm em barras menores. A principio, consideraremos que esses pedaços devem ter a maior quantidade possível, ou seja, temos aqui o conceito de MDC.

MDC(270, 540, 810) = 270

Porém, a questão deseja comprimento menor que 1 m (100 cm).

Podemos dividir o MDC por 3.

270 / 3 = 90 cm

Considerando que as barras terão a medida de 90 cm, podemos calcular a quantidade total.

As barras de 270 cm serão divididas em 3 pedaços de 90 cm cada.

35 barras = 3 x 35 = 105 pedaços

As barras de 540 cm serão divididas em 6 pedaços de 90 cm cada.

18 barras = 6 x 18 = 108 pedaços

As barras de 810 cm serão divididas em 9 pedaços de 90 cm cada.

6 barras = 6 x 9 = 54 pedaços.

Total

105 + 108 + 54 = 267

Resposta: C

Questão 7. Sendo p/q a fração irredutível equivalente a 0,0222… / 0,001818… Qual o valor de p – q?

a) 92.

b) 99.

c) 100.

d) 101.

e) 110.

Resolução

O número 0,222… é uma dízima periódica que equivale a fração 2/9, ou seja, o numerador 0,0222… equivale a fração 2/90, por ser 10 vezes menor.

O número 0,1818… também é uma dízima periódica, e equivale a fração 18/99, ou seja, o denominador 0,001818… equivale a fração 18/9900.

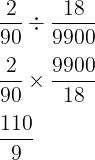
Calculando p – q:

110 – 9 = 101

Resposta: D

Questão 8. Uma escola resolveu confeccionar uma bandeira formada por três faixas horizontais e uma vertical, como
mostra a figura a seguir.

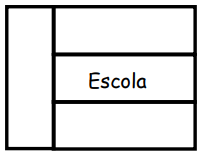
A escola consultou os alunos a respeito das cores a serem usadas na bandeira e foram indicadas cinco
cores. De quantos modos a referida bandeira pode ser pintada, sendo que faixas adjacentes devem ter cores
diferentes?

a) 120.

b) 160.

c) 180.

d) 240.

e) 625.

Resolução

Começaremos a pintar as faixas horizontais, de cima para baixo.

A primeira possui 5 opções de cores.

A segunda possui 4 opções e cores.

A partir daí temos dois casos a considerar:

Caso 1 (todas as cores serão diferentes)

5 x 4 x 3 x 2 = 120

Caso 2 (a faixa horizontal superior possui a mesma cor da inferior)

5 x 4 x 1 x 3 = 60

Total:

120 + 60 = 180

Resposta: C

Questão 9. Uma caixa contém 8 bolas verdes, 6 bolas amarelas, 4 bolas azuis e 2 bolas vermelhas. Qual a probabilidade, de alguém, sem olhar, tirar dessa caixa uma bola azul?

a) 10%.

b) 20%.

c) 40%.

d) 50%.

e) 100%.

Resolução

Observe que a caixa possui 4 bolas azuis e um total de 20 bolas.

A probabilidade de sair uma bola azul é:

4/20 = 0,2 = 20%

Resposta: B

Gostou da prova resolvida do concurso para professor de matemática da Prefeitura de Teresina (NUCEPE – 2019)?

Deixe o seu comentário.