Confira aqui a prova resolvida do concurso para a PM SP 2021, organizado pela Vunesp para o cargo de Soldado.
Boa sorte!
Questão 21. Leia a notícia veiculada em um jornal digital.

Uma frase que substitui corretamente o dado apresentado
na reportagem está indicada em:
(A) 1 em cada 5 metros quadrados onde sistemas de satélite registraram desmate em 2019 no Brasil tem autorização para o corte raso das árvores.
(B) 0,5 em cada 1 000 metros quadrados onde sistemas de satélite registraram desmate em 2019 no Brasil tem autorização para o corte raso das árvores.
(C) 5 em cada 100 metros quadrados onde sistemas de satélite registraram desmate em 2019 no Brasil têm autorização para o corte raso das árvores.
(D) 1 em cada 2 metros quadrados onde sistemas de satélite registraram desmate em 2019 no Brasil tem autorização para o corte raso das árvores.
(E) 1 em cada 200 metros quadrados onde sistemas de satélite registraram desmate em 2019 no Brasil tem autorização para o corte raso das árvores.
Resolução
O texto informa que 0,5% das áreas que registraram desmate em 2019 têm autorização para desmate.
Considerando que a área é medida em metros quadrados, podemos dizer que 0,5 em cada 100 metros quadrados possuem autorização.
Observe que não temos esta opção, porém, “0,5 em cada 100 metros quadrados” é equivalente a “1 em cada 200 metros quadrados”.
Resposta: E
Questão 22. Monges cistercienses desenvolveram no fim do século 13 uma escrita numérica usada em mosteiros de toda a Europa por pelo menos mais de dois séculos. Essa escrita oferecia a possibilidade de representar números com um único símbolo e era baseada nos seguintes caracteres:
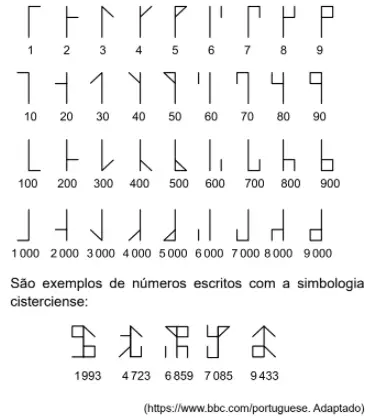
Para poder interpretar o símbolo cisterciense é preciso saber lê-lo, conforme ilustração a seguir:
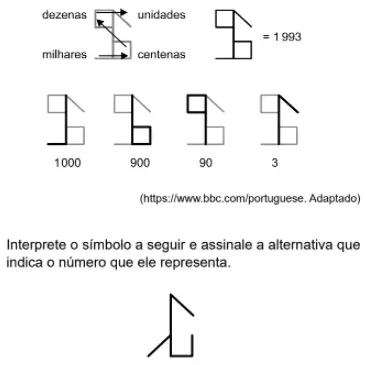
(A) 5630.
(B) 4703.
(C) 4603.
(D) 5703.
(E) 4730.
Resoluçao
Observando a tabela, podemos concluir que o número representado é o 4703.
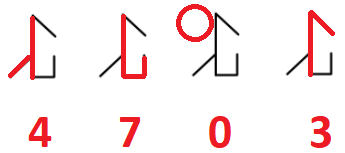
Resposta: B

Questão 23. Uma empresa está propondo a implementação de eletrificação da frota de ônibus coletivos de uma cidade. O projeto envolve a venda do ônibus elétrico e o aluguel da bateria pelo período de 10 anos, no qual a empresa se responsabiliza pelo fornecimento, manutenção e recarga da bateria. Para esse período, o projeto determina um custo de R$1.860.000,00 por ônibus. Segundo a empresa, a grande vantagem desse projeto é que a parte desse custo, referente ao aluguel das baterias, é pago com mensalidades fixas de R$10.000,00, que é o valor aproximado do gasto mensal com diesel dos ônibus convencionais.
Descontado o valor do aluguel da bateria, tem-se que esse projeto considera a venda do ônibus elétrico no
valor de
(A) R$ 1.760.000,00.
(B) R$ 660.000,00.
(C) R$ 760.000,00.
(D) R$ 860.000,00.
(E) R$ 1.740.000,00.
Resolução
10 anos = 120 meses
Considerando que o aluguel das baterias tem um custo mensal de R$ 10.000,00, temos:
120 x R$ 10.000,00 = R$ 1.200.000,00
Sabendo que o custo total foi de R$1.860.000,00, temos:
R$ 1.860.000,00 – R$ 1.200.000,00 = R$ 660.000,00
Resposta: B
Questão 24. Uma reportagem lançada em 2015 trazia que, segundo o Livro Guinness dos Recordes, o lago Maracaibo, na Venezuela, era o lugar com a mais alta concentração de relâmpagos do mundo, com 250 deles por quilômetro quadrado, todo ano. O número de tempestades atinge seu ponto mais espetacular no ápice da estação chuvosa, em
outubro, quando os registros indicam uma média de 40 mil relâmpagos por dia.
Sendo assim, nesses dias de ápice, a média de relâmpagos por minuto é de, aproximadamente,
(A) 16.
(B) 33.
(C) 333.
(D) 275.
(E) 28.
Resolução
Calculando quantos minutos possui um dia:
24 horas x 60 minutos = 1440
Sabendo que em outubro os registros indicaram uma média de 40 mil relâmpagos por dia, temos:
40000 / 1440 = 27,77
Resposta: E
Utilize as informações a seguir para responder às questões de números 25 e 26.
No final de 2020, uma aeronave da Força Aérea Britânica obteve novas imagens do maior iceberg do mundo, enquanto este flutua pelo sul do oceano Atlântico, ao leste da Argentina. Conhecido como A68a, as imagens do iceberg mostraram que o tamanho de sua superfície era de 4,2 mil quilômetros quadrados, um valor 30% menor do que o registrado em julho de 2017, quando o A68a se desprendeu de um bloco de gelo da Antártida.
Questão 25. Quando se desprendeu de um bloco de gelo da Antártida, o tamanho da superfície do iceberg A68a, em milhares de quilômetros quadrados, era igual a
(A) 5,4.
(B) 5,0.
(C) 5,5.
(D) 6,0.
(E) 4,5.
Resolução
As imagens mostraram que a área da superfície do iceberg era de 4,2 km², sendo este valor 30% menor que o registrado em julho de 2017.
Se precisamos saber a área registrada em julho de 2017, basta dividirmos a área de 4,2 por 0,7, que representa que a área equivale a 70% da medição anterior, ou seja, caiu 30%.
4,2 / 0,7 = 6,0
Resposta: D
Questão 26. Considere um campo de futebol retangular, medindo 100 metros de comprimento por 70 metros de largura. A área de 4,2 mil quilômetros quadrados ocupada pelo iceberg no final de 2020 equivale a quantos desses campos de futebol?
(A) 6000000.
(B) 6000.
(C) 600000.
(D) 600.
(E) 60000.
Resolução
Calcularemos a área do campo de futebol em km², sabendo que:
70 metros = 0,07 km
100 metros = 0,1 km
0,1 x 0,07 = 0,007 km²
Para calcularmos quantos campos de futebol caberiam em 4,2 mil km², basta efetuarmos a seguinte divisão:
4200 / 0,007 = 600.000
Resposta: C
Questão 27. Um pequeno cultivador de café está estudando maneiras de agregar valor na venda do café produzido em sua propriedade e aumentar seu lucro. Até então, cada quilograma de café seco vendido retornava um lucro de R$ 3,50 para esse produtor.
Uma alternativa encontrada foi torrar e moer o café a fim de vendê-lo em cápsulas para uso em máquinas de bebidas. Desse modo, ele venderia cada cápsula com 10 gramas de café torrado e moído por R$1,50, sendo que o lucro corresponderia a 3/5 desse valor de venda. Considerando que o processo de torrar e moer 1 kg de café seco elimina 1/4 dessa quantidade, a nova alternativa de venda fará com que o valor do lucro obtido por quilograma do café seco seja de
(A) R$ 67,50.
(B) R$ 64,00.
(C) R$ 86,50.
(D) R$ 112,50.
(E) R$ 90,00.
Resolução
O produtor de café poderia vender 10 gramas de café torrado e moído por R$ 1,50, com lucro correspondente a 3/5 deste valor:
1,50 x 3/5 = R$ 0,90
Segundo a questão, utilizando este processo, torrar e moer 1 kg de café seco elimina 1/4 da quantidade, ou seja, a cada 1 kg, sobrará apenas:
1 kg x 3/4 = 0,75 kg = 750 gramas
Como 10 gramas geram um lucro de R$ 0,90, 750 gramas seriam suficientes para gerar um lucro de:
75 x R$ 0,90 = R$ 67,50
Resposta: A
Questão 28. Os gráficos a seguir apresentam a distribuição da população urbana e rural no mundo e no Brasil.
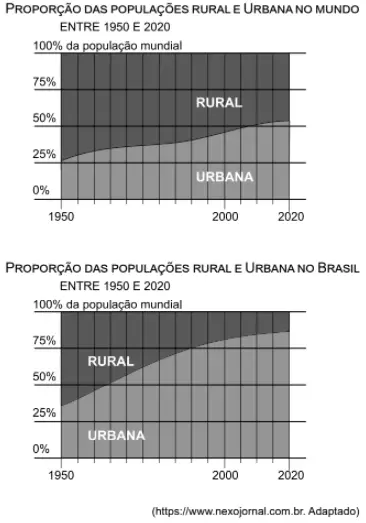
Dado que as marcações verticais relacionadas aos anos de referência estão igualmente espaçadas, ao analisar os dados apresentados, tem-se que a maioria dos habitantes do mundo passaram a viver em áreas urbanas entre os anos de _______________________ , enquanto que, no Brasil, isso ocorreu pouco mais de _________________ anos antes.
Os termos que completam, correta e respectivamente, a frase anterior são:
(A) 2005 e 2010 … 40
(B) 2005 e 2010 … 50
(C) 1995 e 2000 … 50
(D) 2000 e 2005 … 40
(E) 2000 e 2005 … 50
Resolução
Observe na imagem abaixo que a maioria dos habitantes do mundo passaram a viver em áreas urbanas entre os anos de 2005 e 2010.
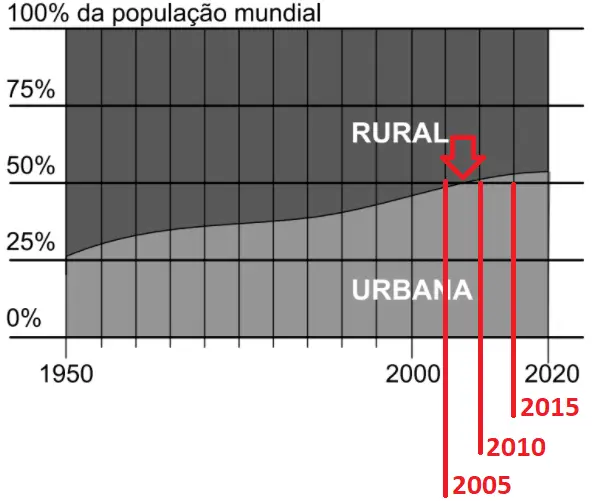
Na figura abaixo é possível observar que, no Brasil, isso ocorreu entre 1960 e 1965, ou seja, pouco mais de 40 anos antes.
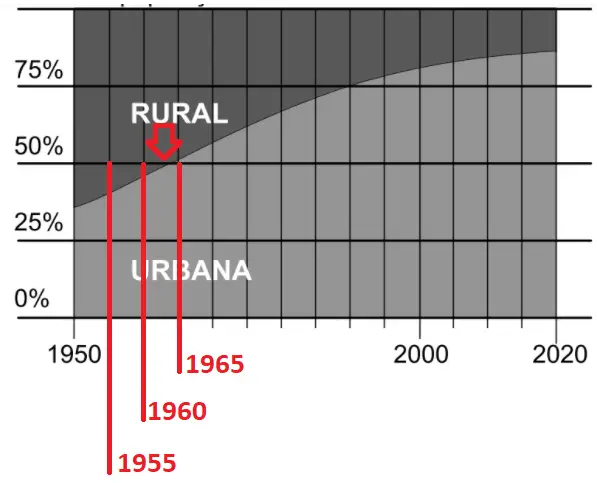
Resposta: A
Questão 29. A pandemia da covid-19 afetou as maiores economias do mundo. Uma das maneiras de perceber isso é o aumento na taxa de desemprego em 2020 quando comparado a 2019. O gráfico a seguir mostra o quanto essa taxa aumentou para 8 países.
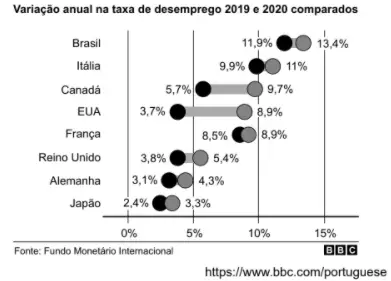
Ao analisar o gráfico, é possível identificar os três países que apresentaram as maiores variações anuais, em pontos percentuais, na taxa de desemprego, sendo que o Brasil ________________ entre eles. Para esses três países, a média das variações anuais na taxa de desemprego foi igual a _________________.
Os termos que completam, correta e respectivamente, a frase anterior são:
(A) está … 11,3 pontos percentuais
(B) está … 2,2 pontos percentuais
(C) não está … 3,8 pontos percentuais
(D) está … 3,5 pontos percentuais
(E) não está … 3,6 pontos percentuais
Resolução
Brasil: 13,4% – 11,9% = 1,5%
Itália: 11% – 9,9% = 1,1%
Canadá: 9,7% – 5,7% = 4,0%
EUA: 8,9% – 3,7% = 5,2%
França: 8,9% – 8,5% = 0,4%
Reino Unido: 5,4% – 3,8% = 1,6%
Alemanha: 4,3% – 3,1% = 1,2%
Japão: 3,3% – 2,4% = 0,9%
As três maiores variações foram nos EUA (5,2%), Canadá (4,0%) e Reino Unido (1,6%). Calculando a média:
(5,2 + 4 + 1,6) / 3 = 10,8 / 3 = 3,6
Resposta: E
Questão 30. Dados do Levantamento Nacional de Informações Penitenciárias de 2014 mostram que a maioria das pessoas presas no referido ano eram homens, e que tanto para homens quanto para mulheres, o tráfico é o principal tipo de crime pelos quais essas pessoas responderam.
Os dois gráficos a seguir retratam essa situação:
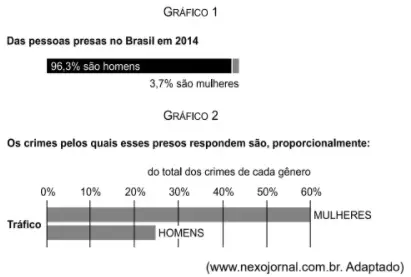
Segundo os gráficos apresentados, das pessoas presas no Brasil em 2014, as mulheres presas que respondem
por tráfico correspondiam a
(A) 2,15%.
(B) 2,22%.
(C) 63,70%.
(D) 2,12%.
(E) 60,00%.
Resolução
O Gráfico 1 informa que 3,7% do total de pessoas presas em 2014 eram mulheres.
O Gráfico 2 informa que 60% das mulheres presas em 2014 foram pelo crime de tráfico.
Se precisamos saber a porcentagem de mulheres presas que respondem por tráfico em relação ao total de presos em 2014, basta multiplicamos estes valores:
3,7% x 60% = 0,037 x 0,6 = 0,0222 = 2,22%
Resposta: B
Questão 31. Uma pesquisa feita com Microempreendedores Individuais (MEI) que encerraram suas atividades teve como objetivo descobrir o principal motivo dessa decisão. Os participantes da pesquisa indicaram um único motivo, sendo que os três motivos mais sinalizados foram:
• 1o motivo: conseguir um emprego
• 2o motivo: não possuir clientes
• 3o motivo: não obter retorno financeiro
Juntos, esses três motivos foram apontados por 54% dos MEI que participaram da pesquisa. Além disso, constatou-se uma diferença de 8 pontos percentuais entre os que indicaram o 1o e o 3o motivo; e que o percentual atribuído ao 2o motivo é igual a média aritmética simples do percentual atribuído ao 1o e 3o motivos.
Sendo assim, conseguir um emprego foi o principal motivo apontado por
(A) 22% dos participantes da pesquisa.
(B) 26% dos participantes da pesquisa.
(C) 18% dos participantes da pesquisa.
(D) 24% dos participantes da pesquisa.
(E) 20% dos participantes da pesquisa.
Resolução
x = 1o motivo: conseguir um emprego
y = 2o motivo: não possuir clientes
z = 3o motivo: não obter retorno financeiro
Se há uma diferença de 8 pontos percentuais entre os que indicaram o 1o e o 3o motivo, então:
x – z = 8
z = x – 8
Como o percentual atribuído ao 2o motivo é igual a média aritmética simples do percentual atribuído ao 1o e 3o motivos, temos que:
y = x – 4
Como os três motivos apontados correspondem a 54%, temos que:
x + y + z = 54
x + (x – 4) + (x – 8) = 54
x + x – 4 + x – 8 = 54
3x – 12 = 54
3x = 54 + 12
3x = 66
x = 66 / 3
x = 22
Resposta: A
Questão 32. Alguns métodos de estimação do tamanho de uma multidão consideram o espaço ocupado por cada pessoa presente no evento. Considere o seguinte método que classifica a multidão nas três categorias a seguir:

Em um evento que ocorreu numa famosa avenida de SP foram estimadas 200 mil pessoas por volta do meio-dia
e 600 mil pessoas ao final da tarde. Considerando que o evento ocupou toda a avenida, que ela é retangular e
possui 2,5 km de comprimento e 40 m de largura, para a realização dessa estimativa, as multidões presentes ao meio-dia e ao final da tarde foram classificadas, respectivamente, como
(A) Multidões densas e Multidões muito densas.
(B) Multidões densas e Multidões densas.
(C) Multidões leves e Multidões densas.
(D) Multidões leves e Multidões muito densas.
(E) Multidões muito densas e Multidões muito densas.
Resolução
Calculando a área da avenida:
2.500 m x 40 m = 100.000 m²
- Foram estimadas 200 mil pessoas por volta do meio-dia:
100.000 / 200.000 = 0,5
Cada pessoa ocupa 0,5 m² (multidões leves)
- Foram estimadas 600 mil pessoas ao final da tarde:
100.000 / 600.000 = 0,16
Cada pessoa ocupa 0,16 m² (multidões muito densas)
Resposta: D
Questão 33. Estudos feitos em 2018 pelo Instituto Trata Brasil, a partir de dados do Sistema Nacional de Informações sobre Saneamento (Snis), mostrou que cerca de 38% da água potável que passa por sistemas de distribuição no Brasil é desperdiçada em vazamentos durante o processo de produção, tratamento e distribuição. Também entram nessa conta desvios ilegais e furtos de água. Esse volume de água equivale a 7 mil piscinas olímpicas de água potável jogadas fora todos os dias.
Considerando que piscinas olímpicas precisam ter um comprimento de 50 metros, uma largura de 25 metros e profundidade mínima de 2 metros, o volume de água potável desperdiçada diariamente nos sistemas de distribuição no Brasil, segundo o estudo citado anteriormente, é de, no mínimo,
(A) 6,65 bilhões de litros.
(B) 2,5 milhões de litros.
(C) 17,5 bilhões de litros.
(D) 17,5 milhões de litros.
(E) 6,65 milhões de litros.
Resolução
Calculando o volume mínimo de uma piscina olímpica:
50 x 25 x 2 = 2500 m³
Sabendo que 1 m³ equivale a 1 mil litros de água, podemos concluir que uma piscina equivale a 2.500.000 litros de água.
A questão informa que o desperdício diário equivale a 7 mil piscinas:
7.000 x 2.500.000 = 17.500.000.000 de litros
Resposta: C
Questão 34. Um artigo científico publicado em 2019 mostrou que o crescimento da população e as mudanças climáticas são dois fatores que pressionam o uso da terra no planeta. Na ocasião, 63,7 milhões de km2 de terra eram destinados à agricultura ou à pastagem, quase a metade do solo não coberto por gelo nas áreas continentais, que totaliza 130 milhões de km2
Sendo que a área destinada à pastagem supera a área direcionada à agricultura em 32,5 milhões de km2, a área voltada para a agricultura ocupa das áreas continentais
(A) mais de 22% do solo não coberto por gelo.
(B) entre 14% e 18% do solo não coberto por gelo.
(C) entre 18% e 22% do solo não coberto por gelo.
(D) entre 10% e 14% do solo não coberto por gelo.
(E) menos de 10% do solo não coberto por gelo.
Resolução
x = área destinada à agricultura
y = área destinada à pastagem
- “63,7 milhões de km2 de terra eram destinados à agricultura ou à pastagem”:
x + y = 63,7
- “a área destinada à pastagem supera a área direcionada à agricultura em 32,5 milhões de km2”:
y – x = 32,5
Subtraindo as duas equações:
x + y – (y – x) = 63,7 – 32,5
x + y – y + x = 31,2
2x = 31,2
x = 31,2 / 2
x = 15,6 milhões de km2
Calculando quanto isto representa do solo não coberto por gelo nas áreas continentais, que totaliza 130 milhões de km2:
15,6 / 130 = 0,12 = 12%
Resposta: D
Questão 35. Um programa de entrevistas é apresentado simultaneamente na TV aberta e por uma plataforma de vídeos, via internet. Devido a essa estratégia, os responsáveis pelo programa vendem tempos distintos de propagandas para serem veiculadas na TV aberta ou na internet, nos intervalos desse programa. Esses intervalos sempre têm mais de 2 minutos de duração, sendo que o programa é retomado simultaneamente nos dois formatos de transmissão, sem a interrupção de anúncios.
As propagandas vendidas para serem veiculadas na internet possuem 15 segundos de duração, enquanto
que as da TV aberta possuem 25 segundos de duração. Assim sendo, o tempo mínimo de duração dos intervalos
desse programa é de
(A) 3 minutos e 45 segundos.
(B) 2 minutos e 30 segundos.
(C) 3 minutos.
(D) 3 minutos e 15 segundos.
(E) 2 minutos e 50 segundos.
Resolução
As propagandas veiculadas na internet possuem 15 segundos de duração, enquanto as da TV aberta possuem 25 segundos.
Como o programa é retomado simultaneamente, precisamos calcular o mínimo valor que seja múltiplo de 15 e 25 simultaneamente, ou seja, o mmc de 15 e 25.
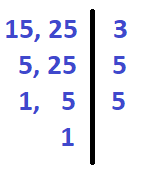
mmc (15, 25) = 3.5.5 = 75 segundos
Observe que 75 segundos equivale a 1 minuto e 15 segundos, ou seja, não respeitaria o intervalo mínimo de 2 minutos.
O próximo número que podemos utilizar será o dobro de 75, que equivale a 150 segundos.
Observe que 150 segundos equivale a 2 minutos e 30 segundos.
Resposta: B
Veja no YouTube:
Gosto da prova resolvida do concurso para a PM SP 2021?
Deixe o seu comentário.
