Confira aqui a prova de matemática resolvida do concurso para a Polícia Militar do Estado de São Paulo (PM SP), aplicada no mês de novembro de 2019. Gabarito Extraoficial.
Boa sorte!
Questão 21. A tabela mostra algumas informações sobre três times de basquete, A, B e C, após cada um deles jogar 5 partidas de um campeonato.
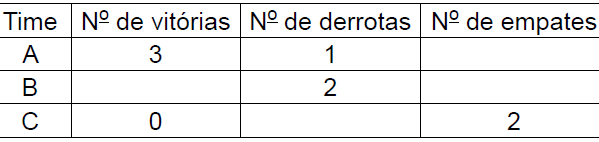
Nesse campeonato, cada vitória soma 3 pontos, cada empate soma 2 pontos, e cada derrota perde 1 ponto. Sabendo que o número de vitórias do time B é igual ao número de empates do time A, então, após essas 5 partidas, a diferença entre os pontos do time A e os pontos do time C é igual a
a) 7
b) 8
c) 9
d) 6
e) 5
Resolução
Considerando que cada time jogou 5 vezes, e que o número de vitórias do time B é igual ao número de empates do time A, podemos preencher a tabela da seguinte forma:
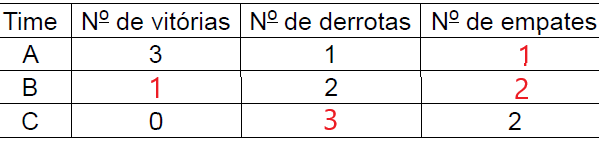
Calculando a pontuação dos times A e C:
A: 3.3 – 1.1 + 1.2 = 9 – 1 + 2 = 10
B: 0.3 – 3.1 + 2.2 = 0 – 3 + 4 = 1
Diferença:
10 – 1 = 9
Resposta: C

Questão 22. João precisa pintar um total de 48 ripas de madeira. Na sexta-feira, ele pintou 3/8 desse total, no sábado, pintou 3/5 das ripas restantes, e, no domingo, pintou as demais, finalizando a pintura. Em relação ao número total de ripas de madeira, aquelas que foram pintadas no domingo correspondem à fração
a) 1/3
b) 1/6
c) 1/8
d) 1/4
e) 1/5
Resolução
Sexta-feira
Quantidade de ripas pintadas
48 . 3/8 = 18
Quantidade de ripas restantes
48 – 18 = 30
Sábado
Quantidade de ripas pintadas
30 . 3/5 = 18
Quantidade de ripas restantes
30 – 18 = 12
Conclusão: João pintou 12 ripas no domingo.
12/48 = 1/4
Resposta: D
Questão 23. Um lote de livros será dividido em caixas, cada uma delas contendo o mesmo número de livros. Pode-se colocar em cada caixa 20 livros, mas também é possível colocar 24 livros em cada uma, ou 25 livros em cada uma, e qualquer que seja a opção, todos os livros do lote ficarão guardados não sobrando livro algum fora das caixas. O menor número de livros desse lote é
a) 480
b) 540
c) 720
d) 660
e) 600
Resolução
A questão não informa a quantidade total de livros, porém sabemos que esses livros podem ser divididos em caixas com 20, 24 ou 25 livros, sem sobra.
Como a banca deseja saber “o menor número de livros desse lote”, basta calcularmos o MMC (mínimo múltiplo comum) de 20, 24 e 25.
MMC (20, 24, 25) = 600
Resposta: E
Questão 24. Uma empresa possui em sua frota 36 veículos. Parte desses veículos são movidos somente a etanol e os demais são movidos somente a gasolina. A razão do número de veículos movidos somente a etanol para o número de veículos movidos somente a gasolina é 5/7. O número de veículos dessa frota movidos somente a gasolina é
a) 21
b) 18
c) 12
d) 15
e) 9
Resolução
Sabendo que a razão entre o número de carros movidos a etanol e o número de carros movidos a gasolina é 5/7, podemos concluir que a cada 12 carros, 5 são movidos a etanol e 7 são movidos a gasolina.
Considerando que a frota possui 36 veículos, temos:
36 . 7/12 = 21
Resposta: A
Questão 25. Uma empresa recebeu 1 200 currículos de candidatos interessados nas vagas oferecidas de emprego e selecionou 35% deles para realizarem uma prova. Sabendo que 15% dos candidatos que fizeram a prova foram contratados, então, o número de candidatos contratados foi
a) 42
b) 49
c) 63
d) 56
e) 70
Resolução
Quantos participaram da prova:
1200 . 35/100 = 420
Quantos foram contratados:
420 . 15/100 = 63
Resposta: C
Questão 26. O gráfico mostra algumas informações sobre o número de unidades vendidas do produto A em 5 dias de uma determinada semana.
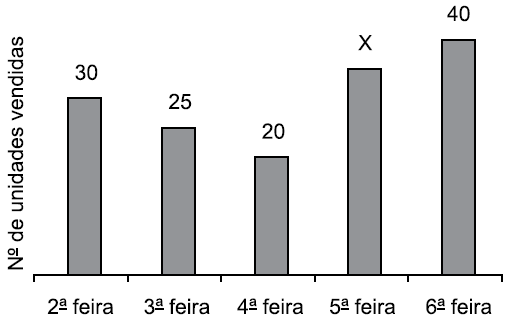
Sabendo que nesses 5 dias foram vendidas, em média, 30 unidades por dia, então, o número de unidades vendidas na quinta-feira foi
a) 45
b) 30
c) 40
d) 35
e) 25
Resolução
Analisando o gráfico, e sabendo que a média é igual a 30 unidades, temos:
(30 + 25 + 20 + x + 40) / 5 = 30
115 + x = 30.5
115 + x = 150
x = 150 – 115
x = 35
Resposta: D
Questão 27. Uma máquina, trabalhando sem interrupções, fabrica 30 peças iguais em 18 minutos. Essa mesma máquina, trabalhando sem interrupções por 2 horas e 48 minutos, irá fabricar uma quantidade de peças igual a
a) 220
b) 280
c) 300
d) 240
e) 260
Resolução
2 horas e 48 minutos = 120 + 48 = 168 minutos
Regra de três
30 peças ————— 18 minutos
x peças —————- 168 minutos
18x = 30.168
18x = 5040
x = 5040/18
x = 280
Resposta: B
Questão 28. Roberta recebeu determinado valor de abono salarial. Gastou, desse valor, 1/5 na farmácia e 1/3 no supermercado, restando ainda R$ 252,00. O valor do abono recebido por Roberta foi
a) R$ 600,00.
b) R$ 630,00.
c) R$ 660,00.
d) R$ 570,00.
e) R$ 540,00.
Resolução
Calculando a fração que representa quanto Roberta gastou na farmácia e no supermercado:
1/5 + 1/3 = (3 + 5)/15 = 8/15
Considerando que x representa o valor do abono, temos:
x . 8/15 = 252
x = 252 . 15/8
x = 540
Resposta: E
Questão 29. Ana e Bete trabalham como vendedoras em uma mesma loja de roupas. Certo dia elas venderam, no total, 54 camisetas. Sabendo que Ana vendeu 8 camisetas a mais do que Bete, então, o número de camisetas vendidas por Ana foi
a) 29
b) 30
c) 31
d) 28
e) 27
Resolução
Sabendo que Ana vendeu 8 camisetas a mais do que Bete, considere que:
x = quantidade de camisas vendidas por Bete
x + 8 = quantidade de camisas vendidas por Ana
Considerando que, no total, foram vendidas 54 camisetas:
x + x + 8 = 54
2x = 54 – 8
2x = 46
x = 46/2
x = 23
Quantidade de camisetas vendidas por Ana:
x + 8 = 23 + 8 = 31
Resposta: C
Questão 30. Um fio de cobre, com 2,7 m de comprimento, foi dividido em 5 pedaços. O 1 o pedaço com 1,3 m de comprimento e os demais pedaços todos de comprimento iguais entre si, conforme mostra a figura.

A diferença entre o comprimento do 1 o pedaço e o comprimento do 2 o pedaço, nessa ordem, é de
a) 65 cm.
b) 75 cm.
c) 85 cm.
d) 105 cm.
e) 95 cm.
Resolução
Sabendo que o comprimento total é de 2,7 metros e que o comprimento do primeiro pedaço é igual a 1,3 metros, podemos concluir que a soma dos demais é igual a:
2,7 – 1,3 = 1,4 metros
Como os demais pedaços possuem comprimentos iguais, temos que:
4x = 1,4
x = 1,4 / 4
x = 0,35 m
Calculando a diferença entre o comprimento do 1o pedaço e o comprimento do 2o pedaço:
1,3 – 0,35 = 0,95 m = 95 cm
Resposta: E
Questão 31. Alfredo foi a uma loja de materiais elétricos para comprar alguns itens. A tabela mostra a quantidade comprada de cada item e seu respectivo valor unitário.
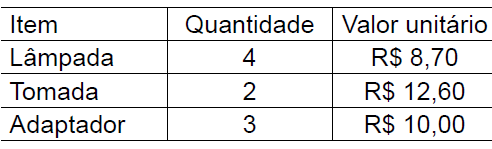
O valor total gasto por Alfredo nessa compra foi
a) R$ 90,00.
b) R$ 92,80.
c) R$ 87,50.
d) R$ 80,00.
e) R$ 83,20.
Resolução
Calculando o valor gasto com cada item:
Lâmpada
4 . 8,70 = 34,80
2 . 12,60 = 25,20
3 . 10,00 = 30,00
Total
34,80 + 25,20 + 30,00 = 90,00
Resposta: A
Questão 32. Um terreno retangular ABCD, com 12 m de comprimento, teve 2/5 de sua área total, reservada para um canteiro de hortaliças, conforme mostra a figura, onde as medidas indicadas estão em metros.
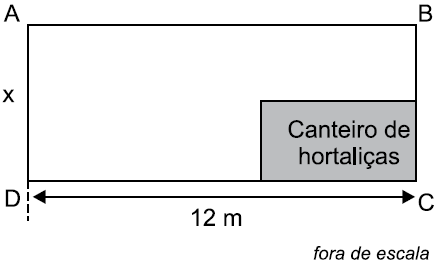
Sabendo que a área do canteiro de hortaliças é 24 m2, então, a medida do lado do terreno, indicada na figura pela letra x, é igual a
a) 6,0 m.
b) 5,5 m.
c) 7,0 m.
d) 5,0 m.
e) 6,5 m.
Resolução
Área total da figura
A = 12x
Considerando que a área do canteiro é 24m2, e que isso representa 2/5 da área total, temos:
12x . 2/5 = 24
24x/5 = 24
x/5 = 1
x = 5
Resposta: D
Questão 33. Uma região retangular foi totalmente cercada por tela. A figura mostra as medidas dos lados, em metros, dessa região.

Se para cercar totalmente essa região foram utilizados 48 m de tela, a medida do lado maior é igual a
a) 8 m
b) 14 m
c) 12 m
d) 10 m
e) 16 m
Resolução
Sabendo que o perímetro do retângulo mede 48 metros, temos:
x + x + x + 4 + x + 4 = 48
4x + 8 = 48
4x = 48 – 8
4x = 40
x = 40/4
x = 10 m
Medida do maior lado:
x + 4 = 10 + 4 = 14 m
Resposta: B
Questão 34. A figura mostra as medidas internas, em centímetros, de um recipiente que tem a forma de um bloco retangular, com 30 cm de altura.
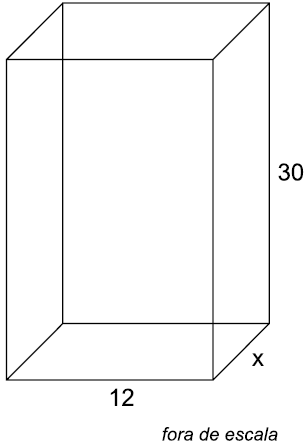
A capacidade total desse reservatório é 2,88 litros. Lembrando que 1 litro = 1 000 cm3 , então, a medida do lado do retângulo da base, indicado na figura pela letra x, é igual a
a) 8 cm.
b) 7 cm.
c) 10 cm.
d) 6 cm.
e) 9 cm.
Resolução
Considerando que 1 litro = 1000 cm3, temos que 2,88 litros corresponde a 2880 cm3.
Calculando o volume do bloco retangular:
12.x.30 = 2880
360x = 2880
36x = 288
x = 288/36
x = 8 cm
Resposta: A
Questão 35. Três amigos, Pedro, José e Caio marcaram de se encontrar na frente de um estádio de futebol, para assistirem a um jogo. Sabe-se que:
– Pedro não foi o último a chegar.
– Caio chegou antes que José.
– Pedro chegou depois de Caio.
Nessas condições, o 1o, o 2o e o 3o a chegar foram, respectivamente,
a) Caio, José e Pedro.
b) Pedro, Caio e José.
c) Caio, Pedro e José.
d) José, Pedro e Caio.
e) Pedro, José e Caio.
Resolução
Como Pedro não foi o último a chegar, porém chegou depois de Caio, podemos concluir que ele foi o segundo a chegar.
Como Caio chegou antes de José, um foi o primeiro e o outro foi o último a chegar.
Ordem correta:
Caio, Pedro, José
Resposta: C
Gostou da prova resolvida da PM SP 2019 (novembro)?
Deixe o seu comentário.
