Confira em primeira mão a prova resolvida do concurso da Polícia Militar do Estado de São Paulo, realizado em 2018 pela Vunesp (PM SP 2018).

Não deixe de ver também em nosso menu outras provas resolvidas de carreiras policiais.

Boa sorte!

Questão 19. Uma loja colocou à venda 80 peças do tipo A e 40 peças do tipo B, e após uma semana havia vendido 1/4 das peças do tipo A e 2/5 das peças do tipo B. Em relação ao número total de peças colocadas à venda, o número de peças que não foram vendidas nessa semana representam

a) 3/10

b) 9/10

c) 3/5

d) 2/5

e) 7/10

Resolução

80 peças do tipo A

40 peças do tipo B

Total de peças: 80 + 40 = 120

Peças não vendidas do tipo A:

80.3/4 = 60

Peças não vendidas do tipo B:

40.3/5 = 24

Total de peças não vendidas:

60 + 24 = 84

Finalizando:

84/120 = 7/10

Resposta: E

Questão 20. A tabela fornece algumas informações sobre o número de vagas abertas e fechadas nos últimos três anos, pelas indústrias de uma determinada cidade.

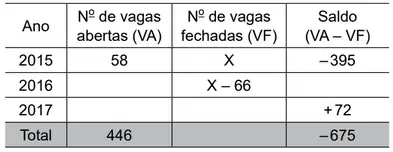
O número de vagas fechadas em 2017 foi

a) 268

b) 276

c) 285

d) 281

e) 272

Resolução

Analisando o ano de 2015:

58 – x = -395

x = 395 + 58

x = 453

Número de vagas fechadas em 2016:

453 – 66 = 387

Total de vagas fechadas (y):

446 – y = – 675

y = 675 + 446

y = 1121

Vagas fechadas em 2017 (z):

453 + 387 + z = 1121

z + 840 = 1121

z = 1121 – 840

z = 281

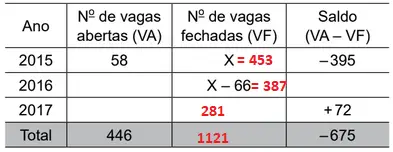
Resposta: D

Questão 21. Em um depósito há um determinado número de caixas que deverão ser empilhadas, de modo que cada pilha tenha o mesmo número de caixas. Na realização da tarefa foi constatado que, se cada pilha tiver 5 caixas, ou 6 caixas ou 8 caixas, sempre restarão 2 caixas fora das pilhas. O menor número de caixas que deverão ser empilhadas nesse depósito é

a) 122

b) 124

c) 118

d) 120

e) 126

Resolução

O total de caixas, quando dividido por 5, 6 ou 8, tem resto sempre igual a 2.

Basta calcularmos o MMC dos três números e adicionarmos duas unidades:

MMC (5, 6, 8) = 120

Total de caixas: 122

Total de caixas nas pilhas: 120

Veja que o enunciado da questão dá margem para duas interpretações diferentes, o total de caixas ou o total de caixas nas 3 pilhas, tornando a questão passível de anulação.

Resposta do gabarito oficial: 122

Questão 22. Uma pessoa tirou 150 fotos com seu celular e excluiu 14 delas. Considerando-se as fotos restantes, a razão entre as fotos de boa qualidade e as fotos de baixa qualidade é 3/5. Sabendo-se que havia somente fotos de boa ou de baixa qualidade no celular, o número de fotos de boa qualidade era

a) 57.

b) 62.

c) 51.

d) 73.

e) 68.

Resolução

Total de fotos restantes:

150 – 14 = 136

Considere que:

x = fotos de boa qualidade

y = fotos de baixa qualidade

Como só existem fotos de boa ou de baixa qualidade:

x + y = 136

Como a razão entre boa e baixa qualidade é 3/5:

x/y = 3/5

5x = 3y

Temos um sistema de equações:

x + y = 136

5x = 3y

Multiplicando a primeira equação por 3 e substituindo os valores da equação 2:

3x + 3y = 408

3x + 5x = 408

8x = 408

x = 408/8

x = 51

Resposta: C

Questão 23. Um determinado produto, se for comprado a prazo, terá 10% de acréscimo sobre o valor da etiqueta, e passará a custar R$ 93,50. Se esse produto for comprado à vista, terá 20% de desconto sobre o valor da etiqueta. O preço desse produto à vista é

(A)    R$ 75,80.

(B)    R$ 68,00.

(C)    R$ 72,50.

(D)    R$ 81,40.

(E)    R$ 79,00.

Resolução

Seja x o valor da etiqueta.

Comprando a prazo:

93,5 = x.1,1

x = 93,5/1,1

x = 85

Comprando à vista:

85.80% = 85.0,8 = R$ 68,00

Resposta: B

Questão 24. Uma máquina trabalhando ininterruptamente 5 horas por dia produz um lote de peças em 3 dias. Para que esse mesmo lote fique pronto em 2 dias, o tempo que essa máquina terá que trabalhar diariamente, de forma ininterrupta, é de

(A)    7 horas e 50 minutos.

(B)    6 horas e 45 minutos.

(C)    6 horas e 35 minutos.

(D)    7 horas e 30 minutos.

(E)    7 horas e 05 minutos.

Resolução

A questão pode ser resolvida através da regra de três simples.

Veja que temos duas grandezas inversamente proporcionais.

2x = 3.5

2x = 15

x = 15/2

x = 7,5 horas

7,5 horas = 7 horas e 30 minutos

Resposta: D

Questão 25. Uma pessoa possui um móvel com algumas gavetas, e quer colocar em cada uma delas o mesmo número de blusas. Ao realizar a tarefa percebeu que, colocando 7 blusas em cada gaveta, 3 blusas ficariam de fora, porém, não seria possível colocar 8 blusas em cada gaveta, pois ficariam faltando 2 blusas na última gaveta. O número total de blusas é

(A)    38.

(B)    30.

(C)    34.

(D)    36.

(E)    32.

Resolução

Considere:

b = quantidade total de blusas

x =  número de gavetas

Analisando as duas situações, temos o seguinte sistema de equações do primeiro grau:

b = 7.x + 3

b = 8.x – 2

Subtraindo a primeira da segunda equação:

b – b = 8x – 7x – 2 – 3

0 = x – 5

x = 5

Calculando a quantidade de blusas:

b = 7x + 3

b = 7.5 + 3

b = 35 + 3

b = 38

Resposta: A

Questão 26. O gráfico apresenta o número de pontos obtidos pelos grupos A, B, C e D, que participaram de uma atividade recreativa.

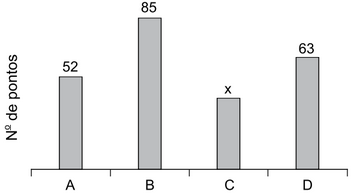
Sabendo que o número de pontos obtidos pelo grupo A foi 30% maior que o número de pontos obtidos pelo grupo C, então, na média, o número de pontos obtidos por um grupo foi

(A)    70.

(B)    50.

(C)    60.

(D)    55.

(E)    65.

Resolução

Calculando o número de pontos do grupo C, considerando que A é 30% maior que C.

C.1,30 = A

C.1,3 = 52

C = 52/1,3

C = 40

Calculando a média:

(52 + 85 + 40 + 63)/4 = 240/4 = 60

Resposta: C

Questão 27. Dois amigos foram a uma lanchonete e pediram cinco pães de queijo e dois sucos, e pagaram, no total, R$ 19,50. Sabendo que o preço de um pão de queijo mais um suco é R$ 6,00, então, o valor a ser pago na compra de três pães de queijo será

(A)    R$ 8,00.

(B)    R$ 7,50.

(C)    R$ 8,50.

(D)    R$ 9,50.

(E)    R$ 9,00.

Resolução

x = preço do pão de queijo

y = preço do suco

Analisando o enunciado, temos um sistema de equações do primeiro grau:

5x + 2y = 19,5

x + y = 6

Da segunda equação:

y = 6 – x

Substituindo na primeira:

5x + 2(6 – x) = 19,5

5x + 12 – 2x = 19,5

3x = 19,5 – 12

3x = 7,50

Resposta: B

Questão 28. Uma avenida retilínea terá um trecho de 3,6 km recapeado, e isso será feito em 3 etapas, conforme mostra a figura.

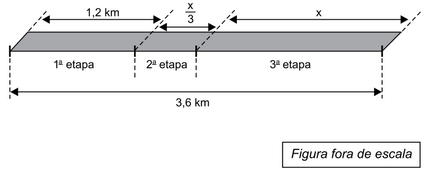
O comprimento do trecho a ser recapeado na 2a etapa é de

(A)    1 200 m.

(B)    1 000 m.

(C)    800 m.

(D)    400 m.

(E)    600 m.

Resolução

Total a ser recapeado nas segunda e terceira etapas:

3,6 – 1,2 = 2,4 km

Na figura, esses dois trechos correspondem a x/3 e x:

x/3 + x = 2,4

4x/3 = 2,4

4x = 2,4.3

4x = 7,2

x = 7,2/4

x = 1,8 km

Comprimento do trecho da segunda etapa:

1,8/3 = 0,6 km = 600 metros

Resposta: E

Questão 29. Uma praça retangular, cujas medidas em metros, estão indicadas na figura, tem 160 m de perímetro.

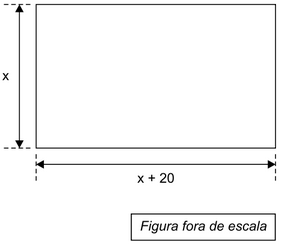
Sabendo que 70% da área dessa praça estão recobertos de grama, então, a área não recoberta com grama tem

(A)    450 m2.

(B)    500 m2.

(C)    400 m2.

(D)    350 m2.

(E)    550 m2.

Resolução

Como o perímetro é igual a 160 metros:

x + x + x + 20 + x + 20 = 160

4x + 40 = 160

4x = 160 – 40

4x = 120

x = 120/4

x = 30 m

Os lados do retângulo medem 30 e 50 metros. Calculando a área:

30.50 = 1500 m²

Como 70% da área dessa praça estão recobertos de grama, então, a área não recoberta com grama corresponde a 30%.

Podemos calcular 30% da área total apenas multiplicando por 0,3:

1500.0,3 = 450 m²

Resposta: A

Questão 30. Um bloco maciço de argila tem a forma de um prisma reto de base retangular e altura igual a 24 cm, conforme mostra a figura.

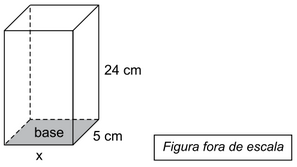
Sabendo que o volume desse bloco é 900 cm3, o perímetro da base indicada na figura mede

(A)    20 cm.

(B)    22 cm.

(C)    15 cm.

(D)    25 cm.

(E)    18 cm.

Resolução

Como o volume é igual a 900 cm³:

24.5.x = 900

120x = 900

x = 900/120

x = 7,5 cm

Perímetro da base:

5 + 5 + 7,5 + 7,5 = 25 cm

Resposta: D

Gostou da prova resolvida do concurso PM SP 2018?

Deixe o seu comentário.