Confira aqui a prova resolvida do concurso para a Polícia Militar do Estado de São Paulo (PM SP 2017), realizado pela Vunesp.
Gabarito extraoficial em primeira mão…
Boa sorte!
Questão 19. Uma pessoa entra no elevador, no piso térreo, e vê no painel que os números -2, -1, 5 e 8 já estão acesos, indicando os andares onde o elevador irá parar. Essa pessoa aperta o botão 12, mas por motivos técnicos, o elevador obedece à seguinte ordem: sai do térreo, indicado pelo número 0, sobe até o 5º andar, desce até o 2º subsolo, indicado pelo -2, depois para o 1º subsolo, indicado pelo número -1, sobe direto até o 8º andar e em seguida sobre até o 12º andar. Sabendo que entre cada andar, a distância percorrida pelo elevador é sempre de 3 metros, então, para fazer o percurso descrito, esse elevador percorreu um total de
a) 81 metros
b) 78 metros
c) 75 metros
d) 69 metros
e) 72 metros
Resolução
Vamos calcular a quantidade de andares percorridos, e por último multiplicaremos por 3 metros.
0 a 5º andar: 5
5º andar ao 2º subsolo: 7
2º subsolo ao 1º subsolo: 1
1º subsolo ao 8º andar: 9
8º andar ao 12º andar: 4
Total: 26
Distância total:
26 . 3 = 78 metros
Resposta: B

Questão 20. Em uma sala havia 120 candidatos fazendo uma prova de certo concurso. Após uma hora do início da prova, 1/5 dos candidatos foi embora. Após mais uma hora, 6 candidatos entregaram a prova e também saíram, e os candidatos restantes permaneceram até o horário limite estabelecido. Em relação ao número inicial de candidatos que havia na sala, aqueles que ficaram até o horário limite estabelecido correspondem a
a) 1/2
b) 1/5
c) 3/5
d) 3/4
e) 1/4
Resolução
Total de 120 candidatos fazendo a prova.
Após 1 hora
1/5 dos candidatos foi embora
120/5 = 24
Restaram 120 – 24 = 96 candidatos
Após 2 horas
6 foram embora
Restaram 96 – 6 = 90
Ficaram até o final / total
90 / 120 = 3/4
Resposta: D
Questão 21. Um comerciante possui uma caixa com várias canetas e irá colocá-las em pacotinhos, cada um deles com o mesmo número de canetas. É possível colocar, em cada pacotinho, ou 6 canetas, ou 8 canetas, ou 9 canetas e, em qualquer dessas opções, não restará caneta alguma na caixa. Desse modo, o menor número de canetas que pode haver nessa caixa é
a) 66
b) 68
c) 72
d) 64
e) 70
Resolução
Não sabemos a quantidade de canetas, mas sabemos que essa quantidade é divisível por 6, 8 e 9, considerando que não restará caneta alguma na caixa em nenhuma das 3 opções.
Como queremos o menor número que seja múltiplo de 6, 8 e 9, basta calcular o mmc desses 3 números.
MMC (6, 8, 9) = 72
Resposta: C
Questão 22. A razão entre o número de camisetas brancas e o número de camisetas pretas vendidas por uma loja, em determinado dia, foi 3/7. Se nesse dia o número total de camisetas vendidas (brancas + pretas) foi 120, então o número de camisetas pretas vendidas foi
a) 75
b) 78
c) 84
d) 88
e) 90
Resolução
b = número de camisetas brancas
p = número de camisetas pretas
Como a razão entre o número de camisetas brancas e pretas é 3/7
b/p = 3/7
b = 3p/7
Como foram vendidas 120 camisetas
p + b = 120
Substituindo a primeira na segunda equação
p + b = 120
p + 3p/7 = 120
7p + 3p = 840
10p = 840
p = 84
Resposta: C
Questão 23. Uma loja comprou um lote com 60 carregadores para telefone celular e vendeu 15% deles na 1ª semana do mês. Entre os demais carregadores, 3 estavam com defeito e foram devolvidos ao fornecedor. Dos carregadores restantes, 75% deles foram vendidos até o final do mês. Após as vendas e a devolução efetuadas, restou ainda um determinado número de carregadores que, em relação ao número de carregadores comprados pela loja, correspondem a
a) 15%
b) 20%
c) 17%
d) 22%
e) 12%
Resolução
A loja comprou 60 carregadores
15% vendidos na primeira semana
60 x 15% = 9
Restaram 60 – 9 = 51
3 foram devolvidos
restaram 51 – 3 = 48
75% vendidos até o final do mês
48 x 75% = 36
restaram 48 – 36 = 12
Carregadores restantes / comprados
12 / 60 = 20%
Resposta: B
Questão 24. Uma indústria possui duas máquinas, A e B, que produzem uma mesma peça. A máquina A produz 7 peças em 15 minutos, e a máquina B produz 8 peças em 20 minutos. Nessas condições, é correto afirmar que, no mesmo tempo gasto pela máquina B para produzir 36 peças, a máquina A irá produzir um número de peças igual a
a) 48
b) 44
c) 46
d) 42
e) 40
Resolução
Máquina A
7 peças em 15 minutos
Máquina B
8 peças em 20 minutos
ou 6 peças em 15 minutos
A máquina B produz 36 peças em:
6 x 15 = 90 minutos
Em 90 minutos a máquina A produz
6 x 7 = 42 peças
Resposta: D
Questão 25. Um estudante fez quatro simulados, A, B, C e D, preparatórios para uma prova de vestibular. A tabela mostra as notas obtidas por ele em cada um dos simulados.
Simulado Nota
A 8
B 8,5
C ?
D 9
Se a média aritmética das quatro notas foi 8,25, então, a nota obtida no simulado C foi
a) 8,25
b) 8,50
c) 7,75
d) 8,00
e) 7,50
Resolução
Calculando a média das notas obtidas nos 4 simulados
(A + B + C + D) / 4 = 8,25
8 + 8,5 + C + 9 = 8,25.4
25,5 + C = 33
C = 33 – 25,5
C = 7,5
Resposta: E
Questão 26. Uma pessoa foi a uma papelaria com R$ 20,00 para comprar canetas, todas de mesmo preço. Ao chegar à papelaria, constatou que, se comprasse 4 canetas e um bloco de anotações gastaria exatamente os R$ 20,00, mas se quisesse comprar somente 6 canetas, não seria possível, pois ficaria faltando R$ 1,00. O valor do bloco de anotações era (em reais)
a) 4,50
b) 5,50
c) 6,00
d) 4,00
e) 5,00
Resolução
Orçamento de 20 reais
Quando a pessoa tentou comprar 6 canetas, faltou 1 real, ou seja, 6 canetas custam R$ 21 reais.
Calculando o valor de cada caneta
21 / 6 = 3,50
Calculando o valor de 4 canetas
4 x 3,5 = 14,00
Como 1 bloco + 4 canetas custam exatamente 20 reais, e 4 canetas custam 14 reais, podemos concluir que o bloco custa:
20 – 14 = 6,00
Resposta: C
Questão 27. Uma loja colocou 80 camisetas em promoção, algumas do modelo A e todas as restantes do modelo B. Nessa promoção, cada camiseta do modelo A estã sendo vendida a 40 reais e cada camiseta do modelo B a 32 reais. Sabendo que o valor arrecadado com a venda das 80 camisetas foi 2840 reais, o número de camisetas do modelo A vendidas foi
a) 35
b) 32
c) 38
d) 30
e) 40
Resolução
80 camisetas na promoção, sendo dois modelos A e B.
Valor do modelo A: 40 reais
Valor do modelo B: 32 reais
Sejam:
x = quantidade de camisas A
y = quantidade de camisas B
Total de 80 camisetas
x + y = 80
y = 80 – x
Valor total arrecadado
40x + 32y = 2840
Substituindo a primeira na segunda equação
40x + 32y = 2840
40x + 32 (80 – x) = 2840
40x + 2560 – 32x = 2840
8x = 2840 – 2560
8x = 280
x = 280 / 8
x = 35
Resposta: A
Questão 28. Uma peça de madeira tem o formato de um prisma reto com 15 cm de altura e uma base retangular com 6 cm de comprimento, conforme mostra a figura.
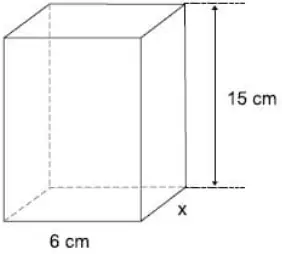
Sabendo que o volume dessa peça é 720 cm³, a área da base é
a) 40 cm²
b) 52 cm²
c) 36 cm²
d) 48 cm²
e) 44 cm²
Resolução
Como trata-se de um prisma reto de base retangular, o volume pode ser calculado multiplicando-se as 3 dimensões.
V = 6 . x . 15
Como o volume é igual a 720 cm³
720 = 6 . x . 15
720 = 90x
x = 720 / 90
x = 8 cm
Área da base
6 . 8 = 48 cm²
Resposta: D
Questão 29. O gráfico mostra o número de unidades de certo produto vendidas nos meses de julho, agosto, setembro e outubro.
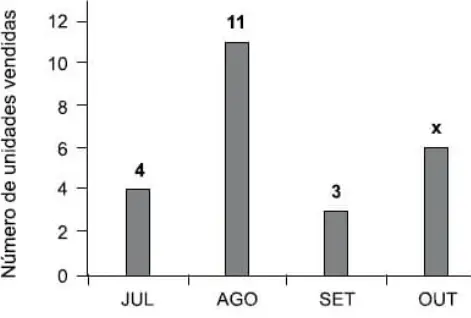
Sabendo que a soma dos valores arrecadados com a venda desse produto nos meses de julho e de setembro foi 840 reais e que o valor arrecadado com as vendas de agosto foi 600 reais a mais do que o valor arrecadado com as vendas de outubro, então, o número de unidades vendidas em outubro foi
a) 6
b) 5
c) 9
d) 7
e) 8
Resolução
Quantidade de produtos vendidos em julho e setembro
4 + 3 = 7
O valor arrecadado nos dois meses foi de 840 reais.
Cada produto foi vendido por
840 / 7 = 120 reais
A diferença entre os valores arrecadados em agosto e outubro foi de 600 reais. Como cada produto custa 120 reais, concluímos que a diferença foi de 5 produtos.
Como foram vendidos 11 produtos em agosto, podemos concluir que a empresa vendeu 6 produtos em outubro.
Resposta: A
Questão 30. O terreno retangular ABCD, mostrado na figura, cujas medidas estão indicadas em metros, tem 80 metros de perímetro.
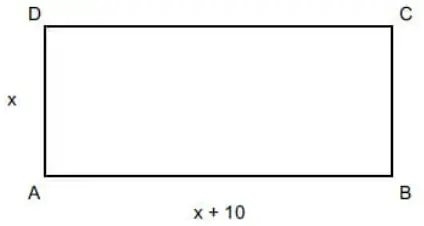
Sabendo que 12% da área desse terreno será destinada à construção de uma garagem, a área dessa garagem será de
a) 38 m²
b) 45 m²
c) 35 m²
d) 42 m²
e) 40 m²
Resolução
Sabendo que podemos calcular o perímetro através da soma dos lados do retângulo, temos:
x + x + (x + 10) + (x + 10) = 80
4x + 20 = 80
4x = 80 – 20
4x = 60
x = 60 / 4
x = 15
Cada lado mede:
x = 15
x + 10 = 25
Área total:
15 . 25 = 375 m²
Área da garagem
375 . 12% = 45m²
Resposta: B
Gostou do gabarito extraoficial (prova resolvida) da PM SP 2017?
Deixe o seu comentário.
