Confira aqui a prova resolvida do concurso para a PM RN (Polícia Militar do Rio Grande do Norte), realizado em 2006 pela CONSULTEC: Consultoria em Projetos Educacionais e Concursos LTDA.
Não deixe de ver na sessão provas resolvidas mais resoluções referentes a concursos para a Polícia Militar de outros Estados.
Bom estudo!
Questão 21. Após receber seu salário de R$ 780,00, um cidadão gasta a metade com aluguel e alimentação e um terço do restante com a escola do filho.
Com base nessa informação, é correto afirmar que sobrará para outras despesas a quantia de
01) R$390,00
02) R$260,00
03) R$240,00
04) R$130,00
05) R$120,00
Resolução
Salário: R$ 780,00
Valor gasto com aluguel e alimentação:
780 / 2 = 390
Valor gasto com escola:
390 / 3 = 130
Valor para outras despesas:
390 – 130 = 260
Resposta: 02
Questão 22. Um indivíduo esqueceu-se da senha de acesso a um computador. Lembrava-se que era formada com as letras A, B, C e D, sem repetição, e que A e B estavam sempre juntas, nessa ordem, e não se lembrava da posição das demais.
Com base nessa informação, pode-se afirmar que a pessoa teria x tentativas para acertar a senha de acesso, portanto x é igual a
01) 2
02) 4
03) 6
04) 8
05) 10
Resolução
Temos 4 letras, que não serão repetidas, com AB sempre juntas e nesta ordem.
Podemos considerar que existem 3 campos a serem preenchidos com AB, C e D.
Total de opções:
3 x 2 x 1 = 6
Resposta: 03
Questão 23. Para demarcar linhas laterais do campo de futebol de um quartel, gasta-se meio litro de solução aquosa de cal para cada metro de marcação.
Sabendo-se que o campo tem formato retangular e que o comprimento e a largura medem 80m e 45m, respectivamente, pode-se afirmar que o total da solução aquosa de cal a ser usada na marcação do campo é igual, em litros, a
01) 125
02) 250
03) 360
04) 480
05) 500
Resolução
Temos um retângulo de perímetro:
80 + 80 + 45 + 45 = 250 m
São gastos 0,5 litros por metro:
0,5 x 250 = 125 litros
Resposta: 01
Questão 24. Numa competição entre três soldados A, B e C, de um quartel, o comandante propôs a resolução das seguintes operações.
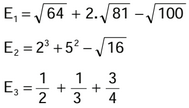
Quem acertasse o resultado de, pelo menos, duas delas, estaria livre do plantão do final de semana do Carnaval. As respostas dadas pelos três soldados, constam da tabela:
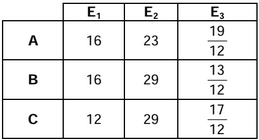
Da análise dessas informações, pode-se concluir:
01) Apenas A estará livre do plantão.
02) Apenas B estará livre do plantão.
03) A dará o plantão.
04) A e C estarão livres no Carnaval.
05) Apenas C dará o plantão.
Resolução
Calculando o valor de cada uma das expressões numéricas:
E1 = √64 + 2.√81 – √100
E1 = 8 + 2.9 – 10
E1 = 8 + 18 – 10
E1 = 16
E2 = 2³ + 5² – √16
E2 = 8 + 25 – 4
E2 = 29
E3 = 1/2 + 1/3 + 3/4
E3 = (6 + 4 + 9) / 12
E3 = 19/12
Os soldados A e B acertaram duas questões cada e estarão livres do plantão.
Resposta: 05
Questão 25. Um reservatório, inicialmente vazio, com capacidade para 8000 litros, recebe água à razão de 1600cm³ por segundo.
O tempo decorrido para que ele fique totalmente cheio é de
01) 1h 20min 40s
02) 1h 21min 30s
03) 1h 22min
04) 1h 23min 20s
05) 1h 24min 40s
Resolução
Para resolvermos a questão, é necessário sabermos que:
– 1 m³ equivale a 1000 litros.
– 0,0016 m³ equivale a 1600 cm³.
O objetivo da questão é encher um reservatório de 8 m³ a uma taxa de 0,0016 m³ por segundo.
8 / 0,0016 = 5000 segundos
Efetuando as devidas transformações, temos que 5000 segundos é equivalente a 1h 23min 20s.
Resposta: 04
Questão 26. Devido a um policiamento ostensivo, a média de criminalidade no Bairro Felipe Camarão, em Natal, caiu linearmente e, depois, manteve-se constante durante certo tempo. O gráfico que melhor ilustra tal variação no índice de criminalidade é
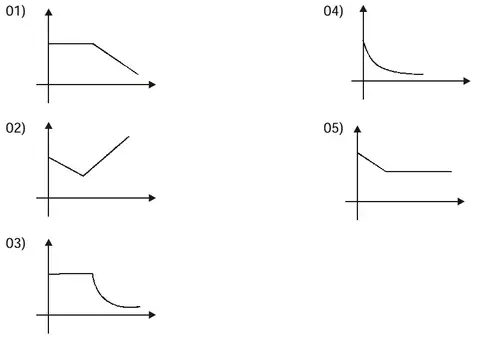
Resolução
Cair linearmente: reta decrescente
Manter-se constante: reta horizontal
Resposta: 05
Questão 27. O gráfico t x I, representa a variação do índice de poluição diária, em Natal, cidade considerada pela NASA como a que possui o “ar mais puro das Américas”.
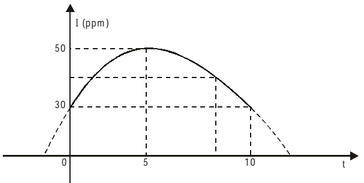
Da análise do gráfico, considerando-se que o instante inicial t = 0 corresponde a 6 horas, pode-se concluir:
01) A função índice é I(t) = t² – 11t + 30.
02) Às 16 horas, o índice era de 30ppm.
03) O índice de poluição, às 10 horas, era de 30ppm.
04) O índice de poluição, às 6 horas, era de 50ppm.
05) O índice máximo ocorreu às 12 horas.
Resolução
Nota-se que o ponto (10, 30) pertence ao gráfico, logo, o índice de poluição, às 10 horas, era de 30ppm.
Resposta: 03
Questão 28. Ao cadastrar os 2000 moradores de um certo bairro, uma equipe constatou que 1100 eram do sexo feminino, 400 eram crianças do sexo masculino e 800 eram adultos.
Com base nesses dados, pode-se afirmar que o número de adultos do sexo masculino era igual a
01) 900
02) 800
03) 700
04) 500
05) 400
Resolução
x = quantidade de adultos do sexo masculino
y = quantidade de adultos do sexo feminino
z = quantidade de crianças do sexo masculino
w = quantidade de crianças do sexo feminino
Pelo enunciado temos:
x + y + z + w = 2000
y + w = 1100
z = 400
x + y = 800
Como z = 400:
x + y + 400 + w = 2000
x + y + w = 2000 – 400
x + y + w = 1600
Restaram 3 equações:
(1) x + y + w = 1600
(2) y + w = 1100
(3) x + Y = 800
Fazendo (1) – (2):
x + y + w – y – w = 1600 – 1100
x = 500
Resposta: 04
Questão 29. A prefeitura do município de Caicó resolveu dar um prêmio de R$ 2800,00 a dois de seus policiais, devido ao trabalho feito por eles na comunidade. O prêmio deve ser dividido em partes diretamente proporcionais ao tempo de serviço de cada um deles, na prefeitura.
Se o primeiro policial tem 8 anos de serviço e o segundo policial tem 6 anos de serviço, então pode-se afirmar:
01) A diferença entre os dois prêmios é de R$300,00.
02) O primeiro deverá receber R$200,00 a mais que o segundo.
03) O segundo policial deverá receber R$1400,00.
04) O segundo policial deverá receber R$1000,00.
05) O prêmio do primeiro policial é aproximadamente 33% maior de que o prêmio do segundo.
Resolução
Sabendo que os valores serão diretamente proporcionais a 8 e 6, e que 8 é aproximadamente 33% maior que 6, temos que a resposta certa é a opção 05.
Resposta: 05
Questão 30. De acordo com o Detran- RN, ainda estão disponíveis os prefixos de placa de automóveis do tipo M _ _.
Se estão disponíveis para a 2a letra X, Y e Z e para a 3a letra A, B, C, D, E, F, G e H, então o número de carros que ainda podem ser emplacados com esse prefixo é
01) 60
02) 36
03) 28
04) 24
05) 18
Número de opções para a segunda letra: 3
Número de opções para a terceira letra: 8
Total de combinações disponíveis: 3 x 8 = 24
Resposta: 04
Questão 31. Se um funcionário público recebe, inicialmente, um salário So e, a cada 2 anos, um aumento de 5% sobre o salário anterior, então a lei que define o salário S do funcionário, em função do tempo t, em biênio, é
01) S(t) = So (1 + 0,5)t
02) S(t) = Sot
03) S(t) = So + 5t
04) S(t) = So(1,05)t
05) S(t) = 5t.So
Resolução
Basta recordarmos a fórmula de juros compostos, onde 5% = 0,05.
Resposta: 04
Questão 32. Para participar da corrida de jegues, que acontece todo mês de setembro na cidade de São Gonçalo de Amarante, um grupo de turistas deseja contratar um ônibus para transportá-los. A empresa A cobra R$120,00 de taxa fixa e mais R$0,60 por quilômetro rodado, enquanto a empresa B cobra R$150,00 de taxa fixa e mais R$0,40 por quilômetro rodado.
Com base nessa informação, pode-se afirmar que a empresa A é mais cara do que a empresa B, se a distância percorrida for maior ou igual a
01) 150km
02) 130km
03) 120km
04) 100km
05) 90km
Resolução
Temos as seguintes funções de custo, onde x é a quilometragem:
Empresa A
CA(x) = 120 + 0,6x
Empresa B
CB(x) = 150 + 0,4x
Calculando a quilometragem que faz o custo ser igual em ambas empresas:
120 + 0,6x = 150 + 0,4x
0,6x – 0,4x = 150 – 120
0,2x = 30
x = 30/0,2
x = 150 km
Veja que a empresa A é mais cara que a empresa B quando a distância percorrida é maior que 150 km, e não maior ou igual. A questão deveria ter sido anulada.
Questão 33. Em uma viatura, quatro policiais fazem o policiamento de uma área em forma de um triângulo cujos vértices são três bairros de Natal, como representados na figura.
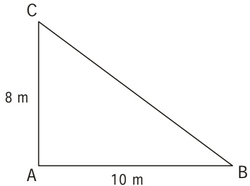
Com base na informação, pode-se afirmar que a área policiada por essa viatura é igual, em unidades de área, a
01) 30
02) 40
03) 45
04) 50
05) 60
O gabarito informa que a resposta correta é 40 m², esta resposta pode ser encontrada se considerarmos que trata-se de um triângulo retângulo, porém em nenhum momento é informado o tipo de triângulo, e nem pode ser deduzido, considerando que existem infinitos triângulos com dois lados medindo 8 e 10 metros.
Questão 34. Na saída da cidade de Mossoró (RN), uma blitz intercepta um caminhão- baú lotado de caixas retangulares, cada uma com 12 garrafas de mel. O comandante da operação ordenou que o soldado contasse quantas garrafas de mel havia no caminhão. O soldado, inteligentemente, simplesmente verificou que o volume interno do baú era igual a 36m³ e que o volume de cada caixa era igual a 36000cm³. Voltou-se ao comandante e disse, com toda certeza, que o número de garrafas era x.
Se o baú estava com a maior quantidade possível de caixas e se a resposta do soldado está correta, 15% de x é igual a
01) 2800
02) 2400
03) 1800
04) 1600
05) 1500
Resolução
Temos que 36000cm³ = 0,036m³. Como a capacidade do baú é de 36m³, podemos concluir que o número de caixas de mel é:
36 / 0,036 = 1000 caixas
Como cada caixa possui 12 garrafas, podemos concluir que existem 12000 garrafas.
15% . 12000 = 1800
Resposta: 03
Questão 35. Suponha-se que, no município de Parnamirim, a Polícia Militar mantenha um pasto para alimentar seus cavalos em forma de um trapézio isósceles cujos lados paralelos medem 300m e 600m.
Se cada um dos lados, não paralelos, medem 50m a menos que o menor dos lados paralelos, então a área, desse pasto, é igual a
01) 90000m2
02) 80000m2
03) 9000m2
04) 8000m2
05) 900m2
Resolução
Analisando as informações do enunciado, temos o seguinte trapézio isósceles.
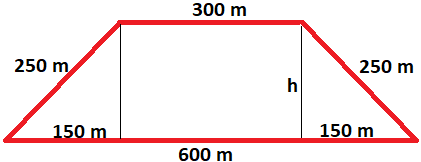
A altura h pode ser calculada através do Teorema de Pitágoras. A medida de 150 m foi calculada subtraindo o menor do maior dos lados paralelos, e dividindo por 2, considerando que trata-se de um trapézio isósceles.
250² = h² + 150²
62500 = h² + 22500
h² = 62500 – 22500
h² = 40000
h = √40000
h = 200 m
Calculando a área do trapézio:
![]()
A = (600 + 300).200 / 2
A = 900 . 100
A = 90000 m²
Resposta: 01
Questão 36. Se, no município de Mossoró, que tem, segundo o censo de 2000, 213841 habitantes, dos quais 14760 vivem na zona rural, então a população urbana, representa um percentual, aproximadamente, de
01) 89%
02) 90%
03) 93%
04) 94%
05) 95%
Resolução
População urbana:
213841 – 14760 = 199081
Calculando a porcentagem:
199081 / 213841 = 0,93 = 93%
Resposta: 03
Questão 37. No campeonato interno de futebol da Polícia Militar do Estado do Rio Grande do Norte, inscreveram-se 32 equipes, divididas em 8 grupos de 4 equipes. Sabendo-se que, na primeira fase, em cada grupo, todos os times se enfrentam e que, em cada jogo, são gastos R$60,00 com arbitragem, pode-se afirmar que o gasto total em arbitragem, na primeira fase do campeonato, será igual a
01) R$2880,00
02) R$2860,00
03) R$2850,00
04) R$2840,00
05) R$2820,00
Resolução
Todos jogam entre si, ou seja, cada uma das 4 equipes jogará 3 vezes, porém devemos dividir por 2 para não contarmos a mesma partida duas vezes.
Total de partidas por grupo:
4 . 3 / 2 = 6
Como existem 8 grupos, teremos um total de:
8 . 6 = 48 partidas
Como cada partida custa 60 reais:
48 . 60 = R$ 2880
Resposta: 01
Questão 38. Numa fase de treinamento, uma tropa policial fazia uma trilha nas redondezas do município de Macau. Cada soldado carregava sacos de igual tamanho e peso. De repente, um dos soldados dirigiu-se a um de seus colegas e disse:
— Minha carga está muito pesada.
O colega respondeu:
— Pare de reclamar, pois se eu te der um dos meus sacos, empataremos em número de sacos. Ao invés disso, se me deres um dos teus, levarei o dobro do número de sacos que tu levas.
Deste modo, se o reclamante carrega x sacos e o seu colega carrega y sacos, então 2x + 3y é igual a
01) 31
02) 28
03) 26
04) 19
05) 7
“se eu te der um dos meus sacos, empataremos em número de sacos”
y – 1 = x + 1
y = x + 1 + 1
y = x + 2
“se me deres um dos teus, levarei o dobro do número de sacos que tu levas”
2(x – 1) = y + 1
2x – 2 = y + 1
2x = y + 1 + 2
2x = y + 3
Substituindo a primeira na segunda equação:
2x = x + 2 + 3
2x – x = 5
x = 5
Calculando o valor de y:
y = x + 2
y = 5 + 2
y = 7
2x + 3y = 2.5 + 3.7 = 10 + 21 = 31
Resposta: 01
Questão 39. Num quartel, para fins estatísticos, foi tirada uma amostragem das massas corporais de policiais com os seguintes resultados em kg 72, 74, 77, 78, 82, 84 e 91.
Desse modo, a massa corporal média foi igual a
01) 77,92kg
02) 78,41kg
03) 79,71kg
04) 80,02kg
05) 81,03kg
(72 + 74 + 77 + 78 + 82 + 84 + 91) / 7 = 558/7 = 79,71 kg
Resposta: 03
Questão 40. Sabe-se que 1 hectare é equivalente a 10.000m², ou seja, a um quadrado de lado 100m. Se os 800.000 habitantes da cidade de Natal fossem uniformemente distribuídos nos 172km² da área da cidade, então é correto afirmar que, em cada hectare, deveriam morar, aproximadamente,
01) 4600 pessoas.
02) 480 pessoas.
03) 460 pessoas.
04) 48 pessoas.
05) 46 pessoas.
Resolução
Temos que 1 hectare é equivalente a 0,01 km².
Calculando a quantidade de hectares da cidade:
172 / 0,01 = 17200 hectares
Quantidade de habitantes por hectare:
800000 / 17200 = 46,5 pessoas
Resposta: 05
Gostou da prova resolvida do concurso para a Polícia Militar do Estado do Rio Grande do Norte, realizado em 2006?
Deixe o seu comentário.
