Confira aqui a prova resolvida do concurso para a Polícia Militar do Estado do Paraná, e elaborada em 2021 pela UFPR para o cargo de soldado.
Boa sorte!
16 – No início do mês de julho, o valor de um produto sofreu um aumento de 10%. No início de agosto, o valor desse produto diminuiu 5% em relação ao mês anterior, fazendo com que ele passasse a custar R$ 250,80. Com base nos dados apresentados, o valor do produto antes do aumento ocorrido no início de julho era de:
a) R$ 237,00.
b) R$ 238,26.
c) R$ 240,00.
d) R$ 245,80.
e) R$ 250,17.
Resolução
Considere que o valor inicial do produto era igual a x.
Com o aumento (julho) de 10%, ele passou a valor 1,1x.
Com a redução (agosto) de 5%, ele passou a valer 1,1x . 0,95 = 1,045x
Sabendo que o preço final do produto passou a ser de R$ 250,80, temos que:
1,045x = 250,80
x = 250,80 / 1,045
x = R$ 240,00
Resposta: C
17 – Três torneiras estão despejando água continuamente. Após 1 minuto, o volume aproximado de água que sai da primeira é de 2,5 cm³, o da segunda é de 3 cm³ e o da terceira é de 4 mL. Quando a primeira torneira tiver despejado 1 L, quantos litros a terceira torneira terá despejado a mais que a segunda?
a) 1,5 L.
b) 1,0 L.
c) 0,7 L.
d) 0,5 L.
e) 0,4 L.
Resolução
Temos três torneiras, que após 1 minuto ligadas, possuem uma vazão de:
Primeira: 2,5 cm³
Segunda: 3 cm³
Terceira: 4 mL
Sabendo que 1 litro corresponde a 1 dm³, que equivale a 1000 cm³, podemos calcular a quantidade de minutos necessários para que a primeira torneira tenha despejado esta quantidade:
1000 / 2,5 = 400 minutos
Agora que sabemos que a primeira demora 400 minutos para despejar 1 litro de água, podemos calcular a quantidade de litros despejados pelas outras torneiras durante este mesmo período:
- Segunda torneira:
400 x 3 cm³ = 1200 cm³
1200 / 1000 = 1,2 litros
- Terceira torneira:
400 x 4 mL = 1600 mL = 1,6 litros
Veja que a terceira despejou 1,6 litros, enquanto a segunda despejou 1,2 litros de água.
1,6 – 1,2 = 0,4 litros
Resposta: E
18 – Em uma pesquisa sobre um determinado tipo de formiga, tomou-se um grupo desses insetos e mediu-se o comprimento de cada um deles. Os dados foram organizados como indica a tabela a seguir.

Sabendo que a média de comprimento dos insetos do grupo foi de 0,6 cm, qual é a quantidade de formigas cujo comprimento é de 0,8 cm?
A) 9
B) 8
C) 6
D) 4
E) 3
Resolução
Calcularemos a média aritmética com as informações apresentadas na tabela:
(0,2×1 + 0,3×3 + 0,4×4 + 0,5×4 + 0,6×3 + 0,7×4 + 0,8xn + 0,9×1)/(1+3+4+4+3+4+n+1) = 0,6
(0,2 + 0,9 + 1,6 + 2 + 1,8 + 2,8 + 0,8n + 0,9)/(20 + n) = 0,6
(10,2 + 0,8n)/(20 + n) = 0,6
10,2 + 0,8n = 0,6(20 + n)
10,2 + 0,8n = 12 + 0,6n
0,8n – 0,6n = 12 – 10,2
0,2n = 1,8
n = 1,8/0,2
n = 9
Resposta: A
19 – Um irrigador distribui água numa região circular, de raio 13,5 m. Devido a um defeito, esse irrigador precisou ser trocado por outro, que passou a irrigar uma região circular de raio 18 m. Assinale a alternativa que representa a área da parte cinza, indicada na figura abaixo, que corresponde à região que passou a ser coberta pelo segundo irrigador, além daquela coberta pelo primeiro.
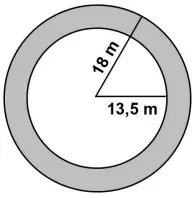
Use π = 22/7.
A) 346,50 m²
B) 396 m²
C) 409,5 m²
D) 445,5 m²
E) 495 m²
Resolução
A área cinza pode ser calculada pela diferença entre a área da região circular de raio 13,5 e a área da região circular de raio 18 m.
A = πR² – πr²
A = π (R² – r²)
A = π (18² – 13,5²)
A = π (324 – 182,25)
A = 141,75π
A = 141,75 x 22/7
A = 445,5 m²
Resposta: D
20 – Um hospital possui duas alas de UTI, totalizando 210 leitos. A primeira destina 25% dos leitos a pacientes infectados pela COVID-19; e a segunda, 50% dos leitos a pacientes com essa doença. Sabe-se que o número total de leitos destinados a pacientes com COVID-19, nas duas UTIs, representa 40% do total de leitos de UTI no hospital. Desse modo, o número de leitos destinados a esses pacientes, na UTI com menor capacidade, é:
A) 15
B) 21
C) 48
D) 63
E) 84
Resolução
Considere:
x = quantidade de leitos de UTI da primeira ala
y = quantidade de leitos de UTI da segunda ala.
Destinados ao COVID-19:
25% de x = 0,25x
50% de y = 0,5y
40% do total de leitos de UTI no hospital:
210 . 40% = 210.4/10 = 84
Considerando as informações acima, temos um sistema de equações do primeiro grau:
x + y = 210
0,25x + 0,5y = 84
Isolando x na primeira equação:
x + y = 210
x = 210 – y
Substituindo x na segunda equação:
0,25x + 0,5y = 84
0,25(210 – y) + 0,5y = 84
52,5 – 0,25y + 0,5y = 84
0,25y = 84 – 52,5
0,25y = 31,5
y = 31,5/0,25
y = 126
Calculando o valor de x:
x = 210 – y
x = 210 – 126
x = 84
A menor ala, representada por x, possui 84 leitos, dos quais 25% são destinados ao COVID-19:
84 . 25% = 21 leitos
Resposta: B
21 – Considere a tabela e o gráfico que descrevem a capacidade de armazenamento de grãos de quatro cooperativas:
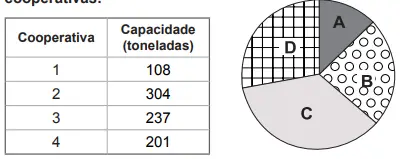
De acordo com o gráfico de setores, à direita da tabela, as regiões A, B, C e D correspondem respectivamente às seguintes cooperativas:
A) 2, 3, 4, 1
B) 4, 1, 2, 3
C) 2, 4, 3, 1
D) 1, 3, 4, 2
E) 1, 4, 2, 3
Resolução
Podemos ordenar as cooperativas por capacidade, conforme tabela:
304 toneladas – cooperativa 2
237 toneladas – cooperativa 3
201 toneladas – cooperativa 4
108 toneladas – cooperativa 1
Podemos também ordenar as regiões A, B, C e D por tamanho, da maior para a menor, conforme gráfico de setores:
C, D, B, A
C: cooperativa 2
D: cooperativa 3
B: cooperativa 4
A: cooperativa 1
Resposta: E
22 – A figura abaixo ilustra um corrimão instalado numa rampa de acesso.
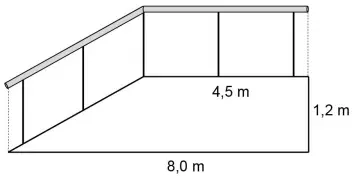
Com base nessa figura, o comprimento do corrimão é de:
A) 5,7 m
B) 6,9 m
C) 7,8 m
D) 8,2 m
E) 9 m
Resolução
Calcularemos inicialmente a medida do comprimento do pedaço de corrimão (x) que está localizado na parte inclinada:
x² = 1,2² + 3,5²
x² = 1,44 + 12,25
x² = 13,69
x = √13,69
x = 3,7
Para finalizar, basta adicionarmos a medida da parte do corrimão que equivale a 4,5 m:
3,7 + 4,5 = 8,2 m
Resposta: D
23 – Geraldo e Maurício possuem coleções de cartões postais de regiões do Paraná. A coleção de Geraldo pode ser organizada em um álbum, colocando-se 3 cartões por folha. Usando o mesmo número de folhas, pode-se organizar a coleção de Maurício, colocando-se 5 cartões por folha. Além disso, se Maurício der 6 cartões de sua coleção a Geraldo, as coleções de ambos passarão a ter a mesma quantidade de cartões. Quantos cartões há nas coleções de Geraldo e Maurício juntas?
A) 48
B) 33
C) 27
D) 23
E) 14
Resolução
Considere que x representa a quantidade de cartões de Geraldo e que y representa a quantidade de cartões de Maurício.
Se considerarmos que k representa a quantidade de folhas do referido álbum, teremos as seguintes relações:
3k = x
5k = y
Dividindo uma equação pela outra:
3k/5k = x/y
x/y = 3/5
5x = 3y
Sabendo que “se Maurício der 6 cartões de sua coleção a Geraldo, as coleções de ambos passarão a ter a mesma quantidade de cartões”, temos que:
y – 6 = x + 6
y = x + 6 + 6
y = x + 12
Observe que temos um sistema de equações do primeiro grau com duas incógnitas:
5x = 3y
y = x + 12
Substituindo a segunda na primeira equação:
5x = 3y
5x = 3(x + 12)
5x = 3x + 36
5x – 3x = 36
2x = 36
x = 36/2
x = 18
Calculando o valor de y:
y = x + 12
y = 18 + 12
y = 30
Calculando quantos cartões há nas coleções de Geraldo e Maurício juntas:
18 + 30 = 48
Resposta: A
24 – Uma região de plantio possui formato retangular. Ampliando seu lado menor em 8 m, obteve-se uma nova região retangular, conforme ilustra a figura ao lado. O perímetro da região ampliada passou a ser de 242 m, e sua área ficou 20% maior que a área da região inicial.
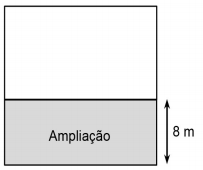
Com base nisso, o perímetro da região cinza, que corresponde à ampliação feita, é de:
A) 113 m
B) 146 m
C) 162 m
D) 210 m
E) 226 m
Resolução
Sejam x e y os lados do retângulo inicial, conforme figura abaixo:
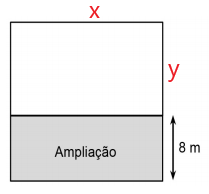
Considerando que o perímetro da região ampliada passou a ser de 242 m, temos:
x + x + y + 8 + y + 8 = 242
2x + 2y + 16 = 242
2x + 2y = 242 – 16
2x + 2y = 226
x + y = 113
Considerando que a área ficou 20% maior que a área da região inicial, podemos considerar que a área ampliada (8x) corresponde a 20% da área inicial (xy):
0,2.xy = 8x
0,2y = 8
y = 8/0,2
y = 40
Podemos calcular o valor de x através da equação anterior:
x + y = 113
x + 40 = 113
x = 113 – 40
x = 73
Perímetro da região cinza:
73 + 73 + 8 + 8 = 162
Resposta: C
25 – Em uma pesquisa sobre a preferência pelos sabores laranja, maracujá ou uva, dos sucos comercializados por uma empresa, foram entrevistadas 70 pessoas, pedindo-se que cada uma delas manifestasse preferência por até 2 sabores. Sabe-se que 5 pessoas não quiseram participar da pesquisa; 19 escolheram apenas o sabor laranja; 12, apenas o sabor maracujá; 16, apenas o sabor uva; e 7, os sabores de maracujá e laranja. Dos entrevistados, quantos escolheram exatamente dois sabores, sendo um deles uva?
A) 9
B) 11
C) 12
D) 16
E) 18
Resolução
Analisando o enunciado, podemos desenhar o seguinte diagrama:
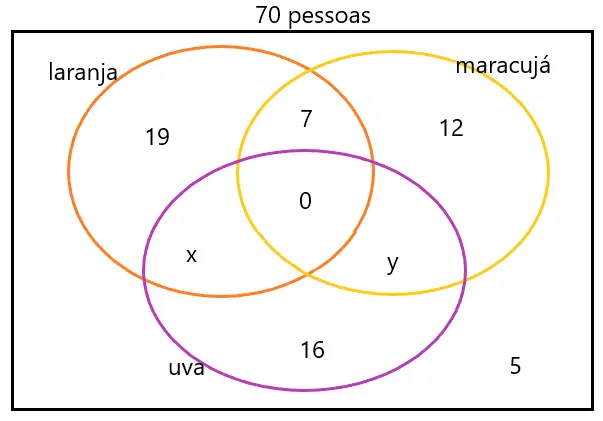
Observe que o objetivo é calcular quantos escolheram exatamente dois sabores, sendo um deles uva, ou seja, o nosso objetivo será calcular o valor de x + y.
Como foram entrevistadas 70 pessoas, sendo que 5 não quiseram responder, temos que:
19 + 7 + 12 + 16 + 5 + x + y = 70
x + y + 59 = 70
x + y = 70 – 59
x + y = 11
Resposta: B
26 – Uma primeira urna possui uma bola branca e duas pretas. Uma segunda urna possui duas bolas brancas e uma preta. Uma terceira urna, por sua vez, possui uma bola branca e uma preta. Uma pessoa vendada retira uma bola da primeira urna e a coloca na segunda. Em seguida, retira uma bola da segunda urna e a coloca na terceira. Por fim, retira uma bola da terceira urna.
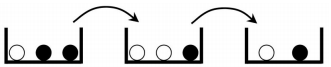
Sabendo que todas as bolas são idênticas em forma e peso, quantas possibilidades há de que a bola retirada da terceira urna seja preta?
A) 5
B) 8
C) 14
D) 15
E) 18
Resolução
Temos 4 casos a analisar:
- PPP
Retirar uma bola PRETA (em duas possíveis) da primeira urna.
Retirar uma bola PRETA (em duas possíveis, considerando a que foi retirada da primeira urna) da segunda urna.
Retirar uma bola PRETA (em duas possíveis, considerando a que foi retirada da segunda urna) da terceira urna.
2 x 2 x 2 = 8
- BPP
Retirar uma bola BRANCA da primeira urna.
Retirar uma bola PRETA da segunda urna.
Retirar uma bola PRETA (em duas possíveis, considerando a que foi retirada da segunda urna) da terceira urna.
1 x 1 x 2 = 2
- PBP
Retirar uma bola PRETA (em duas possíveis) da primeira urna.
Retirar uma bola BRANCA (em duas possíveis) da segunda urna.
Retirar uma bola PRETA da terceira urna.
2 x 2 x 1 = 4
- BBP
Retirar uma bola BRANCA da primeira urna.
Retirar uma bola BRANCA (em três possíveis, considerando a que foi retirada da primeira urna) da segunda urna.
Retirar uma bola PRETA da terceira urna.
1 x 3 x 1 = 3
Total:
8 + 2 + 4 + 3 = 17
Não existe alternativa com a resposta correta.
A questão deve ser anulada.
27 – Um recipiente possui formato de um cubo de aresta 12 cm. Há no recipiente 0,944 L de água e, no fundo, um dado também de formato cúbico, com aresta medindo 2 cm. Se o dado for retirado do recipiente, a altura do líquido nesse recipiente será de aproximadamente:
A) 11,4 cm
B) 7 cm
C) 6,5 cm
D) 6 cm
E) 5,7 cm
Resolução
Considere inicialmente que 0,944 L é igual a 944 mL.
Para resolvermos a questão, devemos saber previamente que 1000 mL equivalem a 1000 cm³, ou seja, 944 mL equivalem a 944 cm³.
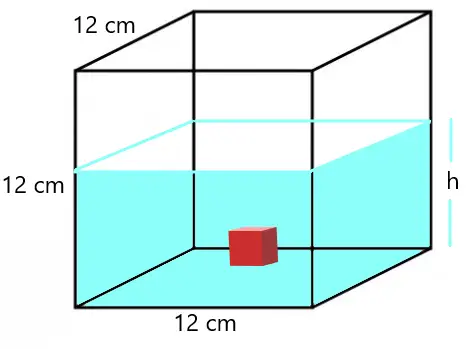
Sabendo que o recipiente tem o formato de um cubo de aresta 12 cm, e que a água mais o dado possuem volume de 944 cm³, podemos calcular a altura h:
12 x 12 x h = 944
h = 944 / 144
h = 6,55 cm
Para finalizar, devemos calcular a altura após a retirada do dado. Calculando inicialmente o seu volume:
2 x 2 x 2 = 8 cm³
Veja que o volume do dado é igual a 8 cm³. Calcularemos a altura H relativa a este volume em um cubo de 12 cm de aresta
12 x 12 x H = 8
144 x H = 8
H = 8/144
H = 0,05 cm
Calculando a altura após a retirada do dado:
h – H = 6,55 – 0,05 = 6,5 cm
Resposta: C
Gostou da resolução da prova da Polícia Militar do Estado do Paraná (PM PR 2021)?
Deixe o seu comentário.
