Confira aqui a prova resolvida do concurso para a Polícia Militar do Estado do Piauí (PI) realizado em 2009 pela Nucepe.
A banca foi muito feliz ao cobrar vários assuntos interessantes, além de acertar no nível que o concurso exige.
Bom estudo!
Questão 19. Considerando o conjunto universo U = {2, 4, 6, 8, 10} e os conjuntos não-vazios A e B, subconjuntos de U, tais que B⊂A, A U B = {6, 8, 10} e A ∩ B = {8}, pode afirmar, CORRETAMENTE, que A é:
a) {6,8,10}
b) {4,6}
c) {4,6,8}
d) {2,6,10}
e) {6,8}
Resolução
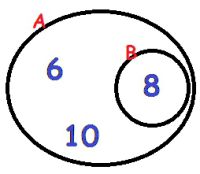
Com as informações apresentadas pela questão, podemos representar os conjuntos A e B da seguinte forma:
Observando o desenho, temos que:
A = {6, 8, 10}
Resposta: A
Resolução
O conjunto A é formado pelos números Reais maiores ou iguais a 1 e menores que 10.
O conjunto B é formado pelos valores de x que fazem (x+1).(x-6) < 0.
(x+1).(x-6) < 0
x² – 6x + x – 6 < 0
x² – 5x – 6 < 0
Calculando as raízes da equação x² – 5x – 6 = 0
Δ = b² – 4ac
Δ = (-5)² – 4.1.(-6)
Δ = 25 + 24
Δ = 49
Se analisarmos o gráfico da função f(x) = x² – 5x – 6, temos uma parábola com cavidade para cima (a > 0) e com raízes -1 e 6, logo, o conjunto B é formado pelos números Reais maiores que -1 e menores que 6.
O conjunto C é formado pelos valores de z que fazem z² = 6z, ou seja, z = 6.
Conclusão:
A = [1, 10[
B = ]-1, 6[
C = {6}
Logo,
A ∩ (C U B) = [1, 10[ ∩ ]-1, 6] = [1, 6]
Resposta: E
21. Sobre o preço de uma moto importada incide um imposto de importação de 30%. Em função disso, o seu preço para o importador é de R$ 15.600,00. Supondo que tal imposto passe de 30% para 60%, qual será, em reais, o novo preço da moto, para o importador?
a) 19.200,00
b) 22.500,00
c) 31.200,00
d) 39.000,00
e) 21.000,00
Resolução
Chamando de x o valor sem impostos e sabendo que para aumentar 30% basta multiplicarmos por 1,30, temos que:
x.1,30 = 15600
x = 15600/1,3
x = 12000
Vamos agora aplicar 60% sobre os 12000:
12000.1,60 = 19200,00
Resposta: A
22. José comprou um sítio de 14 hectares, reservando, para a construção da casa e área de lazer, 1/4 do terreno. O restante, José usou para plantar arroz, milho e feijão. Se a área plantada tem 2/7 de arroz e 3/5 de milho, quantos metros quadrados do terreno foram ocupados com a plantação de feijão?
Dado: 1 hectare = 10000 m²
a) 140.000 m²
b) 72.000 m²
c) 105.000 m²
d) 12.000 m²
e) 25.000 m²
Resolução
Se ele reservou 1/4 para a construção, então restaram 3/4 para a plantação:
14 hectares x 3/4 = 14 x 3/4 = 42/4 = 10,5 hectares
Desses 10,5 hectares ele plantou 2/7 de arroz, 3/5 de milho e feijão no restante:
2/7 + 3/5 = (10 + 21)/35 = 31/35
Logo, sobraram 4/35 para o feijão.
10,5 hectares x 4/35 = 10,5 x 4/35 = 42/35 = 6/5 hectares.
Como 1 hectare = 10000 m²:
10000.6/5 = 60000/5 = 12000 m²
Resposta: D
23. Dados:
Definição 1: A equação ax + by = c, onde a, b e c são números inteiros conhecidos, e x e y são variáveis que só assumem valores inteiros, chama-se Equação Diofantina.
Definição 2: Os números inteiros a e b são primos entre si e os únicos divisores comuns de a e b são 1 e –1.
Afirmação: A equação Diofantina ax + by = c tem solução se, e somente se, a e b forem primos entre si.
A solução da equação 8x + 15y = 54 é:
a) (2,3)
b) (4,1)
c) (1,4)
d) (3,2)
e) (1,3)
Resolução
Basta verificar que o único par que satisfaz a equação é o (3,2):
8x + 15y = 548.3 + 15.2 = 54
Resposta: D
24. Um quartel de polícia tem 750 soldados e comprou marmitas individuais congeladas suficientes para o almoço destes durante 25 dias. Se esse quartel de polícia tivesse mais 500 soldados, a quantidade de marmitas já adquiridas seria suficiente para um número de dias igual a:
a) 15
b) 13
c) 12
d) 18
e) 20
Resolução
Temos que a quantidade de marmitas alimenta 750 soldados em 25 dias.
Se aumentarmos 500 soldados, teremos 1250, logo, a mesma quantidade de marmitas durará menos dias (temos duas grandezas inversamente proporcionais).
Utilizando a regra de três:

1250x = 750.25
1250x = 18750
x = 17500/1250
x = 15 dias
Resposta: A
25. Uma empresa de cosmético possui R$ 80.000,00. Ela aplica 30% desse dinheiro em um investimento que rende juros simples a uma taxa de 3% ao mês, durante 2 meses; e aplica o restante em outro investimento que rende 2% ao mês durante 2 meses também. Ao fim desse período, esse investidor possui:
a) R$ 83.000,00
b) R$ 84.300,00
c) R$ 85.200,00
d) R$ 86.300,00
e) R$ 83.680,00
Resolução
O valor foi dividido em dois investimentos distintos.
Calcularemos inicialmente o valor de cada um.
80000 x 30% = 80000 x 30/100 = 2400000/100 = 24000
80000 x 70% = 80000 x 70/100 = 5600000/100 = 56000
Aplicação 1
24000 a 3%, durante 2 meses:
24000 x 3% = 24000 x 3/100 = 72000/100 = 720
Em dois meses:
2 x 720 = 1440
Aplicação 2
56000 a 2%, durante 2 meses:
56000 x 2% = 56000 x 2/100 = 112000/100 = 1120
Em dois meses:
2 x 1120 = 2240
Total de juros:
1440 + 2240 = 3680
Saldo final:
80.000 + 3.680 = 83.680
Resposta: E
26. No alto de uma torre de uma emissora de televisão duas luzes “piscam” com frequências diferentes. A primeira, “pisca“ 12 vezes por minuto e a segunda, “pisca“ 15 vezes por minuto. Se num certo instante as luzes piscam simultaneamente, após quantos segundos elas voltarão a piscar simultaneamente?
a) 10 segundos.
b) 20 segundos.
c) 15 segundos.
d) 40 segundos.
e) 30 segundos.
Resolução
A luz que pisca 12 vezes por minuto pisca de 5 em 5 segundos.
60 / 12 = 5 segundos
Ela pisca em 0, 5, 10, 15, 20…
A luz que pisca 15 vezes por minuto pisca de 4 em 4 segundos.
60 / 15 = 4 segundos
Ela pisca em 0, 4, 8, 12, 16, 20…
Precisamos simplesmente calcular o mmc de 4 e 5 que é 20.
Resposta: B
27. A expressão √18 + √50 é equivalente:
a) 2√2
b) 3√2
c) 8√2
d 15√2
e) 8√3
Resolução
Fatorando os números dentro das raízes, temos que:
18 = 2.3²
50 = 2.5²
√18 + √50 = √(2.3²) + √(2.5²) = 3√2 + 5√2 = 8√2
Resposta: C

A questão deveria ter sido anulada.Basta observar que o numerador é negativo e o denominador é positivo, resultando em uma resposta negativa.
29. O valor de a para que o sistema (3x + 2y =1; ax – 4y = 0) seja compatível e determinado é:
a) a = 6
b) a = -6
c) a diferente de -6
d) a = 3
e) a diferente de 3
Resolução
Se considerarmos a = -6, teremos:
-6x – 4y = 0
que é equivalente a 3x + 2y = 0.
Veja que esta última contradiz a primeira equação do sistema.
Logo, a deve ser diferente de -6.
Resposta: C
30. Um prisma triangular regular tem a medida da aresta da base igual à medida da aresta lateral. Se a área total do prisma é 2( 6 + √3 ) cm², então a altura do prisma é:
a) 2 cm
b) 3 cm
c) 6 cm
d) 10 cm
e) 9 cm
Resolução
O prisma regular em questão é o que aparece na imagem abaixo. Observe que todas as arestas são iguais, pois a banca informa que a medida da aresta da base é igual à medida da aresta lateral.
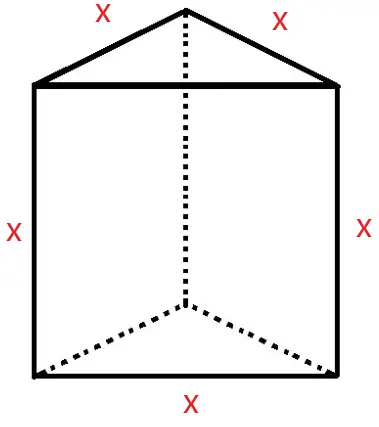
Veja que consideramos que x é a medida de todas as arestas, inclusive a que representa a altura do prisma regular.
A área total deste prima pode ser calculada observando-se que ele possui duas faces triangulares (triângulo equilátero), e três faces quadradas.
Área do quadrado:
A = x²
Área do triângulo:
Utilizando a fórmula da área do triângulo equilátero, temos que:
A = √3x²/4
Área total:
At = 3 . x² + 2 . √3x²/4
At = 3x² + √3x²/2
Para calcularmos a altura (valor de x), basta observarmos que a questão informou o valor da área total:
3x² + √3.x²/2 = 2( 6 + √3 )
(6x² + √3.x²)/2 = 2( 6 + √3 )
6x² + √3.x² = 2.2( 6 + √3 )
6x² + √3.x² = 4( 6 + √3 )
x²(6 + √3) = 24 + 4√3
x² = (24 + 4√3) / (6 + √3)
x² = 4(6 + √3) / (6 + √3)
x² = 4
x = √4
x = 2
Resposta: A
Gostou da prova resolvida do concurso para a Polícia Militar do Estado do Piaúi (PM PI), organizado em 2009 pela NUCEPE?
Deixe o seu comentário.


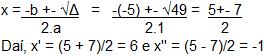
qual a resolução da 30