Olá caros estudantes!
Para quem está se preparando para o próximo concurso para a Polícia Militar do Estado de Pernambuco (PM PE), acompanhar a prova resolvida é uma ótima dica.
O concurso está super disputado e, como sempre, a matemática costuma desequilibrar…
Bons estudos e boa sorte a todos!
31. Carlos disse a Renato que era capaz de acertar um número que ele pensasse, fazendo, apenas, 4 perguntas. Renato achou graça e disse: pensei em um número. Então, Carlos disse: some ao número pensado o número 5, multiplique a soma por 3 e subtraia 10 do produto. Informe o resultado das operações, e Renato afirmou 80. Carlos, então, informou corretamente o número que Renato havia pensado. O produto dos algarismos do número que Renato pensou é igual a
A) 12
B) 15
C) 10
D) 48
E) 50
Solução.
Seja x o número que Renato pensou.
Some 5 ao número: x + 5
Multiplique por 3 a soma: 3(x + 5)
Subtraia 10 do produto: 3( x + 5) – 10
Informe o resultado: 3(x + 5) – 10 = 80
Basta resolvermos a equação do primeiro grau:
3(x + 5) – 10 = 80
3x + 15 = 80 + 10
3x = 90 15
3x = 75
x = 25
O valor pensado é 25, e o produto dos algarismos é 10.
Resposta: C
32. Sr. Jairo tem três filhos: Pedro, Carlos e José. A razão entre as idades de Pedro e Carlos é 1/3 nessa ordem, e a razão entre as idades de José e Carlos é 1/2. Sabendo-se que a soma das respectivas idades é 99 anos, é correto afirmar que a soma dos algarismos da idade de Carlos é
A) 9
B) 12
C) 11
D) 16
E) 10
Solução.
Sejam:
P = Idade de Pedro
C = Idade de Carlos
J = idade de José
De “A razão entre as idades de Pedro e Carlos é 1/3”, temos:
P/C = 1/3
Daí, P = C/3
De “a razão entre as idades de José e Carlos é 1/2”, temos:
J/C = 1/2
Daí, J = C/2
De “a soma das respectivas idades é 99 anos”, temos:
P + C + J = 99
Substituindo:
P + C + J = 99
C/3 + C + C/2 = 99
Multiplicando tudo por 6:
2C + 6C + 3C = 594
11C = 594
C = 594/11
C = 54
Assim, a soma dos algarismos da idade de Carlos é:
5 + 4 = 9
Resposta: A
33. Carlos e Pedro são alunos muito aplicados em matemática. Certo dia, Carlos perguntou a Pedro se ele sabia resolver a seguinte questão: Determine o algarismo das unidades do número (8325474)^(642). Pedro resolveu o problema, chegando ao resultado correto. Qual foi o resultado a que Pedro chegou?
A) 4
B) 2
C) 5
D) 6
E) 1
Solução
Se a e n são inteiros positivo a^n = a. a. a. a. . . a( n vezes)
Toda potência de um número inteiro e positivo, cujo algarismo das unidades é 4, tem como algarismo das unidades 6 ou 4.
Veja:
(14)¹ = 14
(14)² = 196
(14)³ = 2744
(14)^4 = 38416
Nota-se que existe um padrão no algarismo da unidade.
Quando o expoente é ímpar, o algarismo é 4.
Quando o expoente é par, o algarismo é 6.
Temos então que o algarismo da unidade de (8325474)^(642) é 6, pois o expoente é 642, que é um número par.
Resposta: D
34. Para construir sua casa de praia, Fernando contratou a Construtora More Bem. No contrato, ficou estabelecido que a casa seria entregue em 8 meses, e, se a construtora não cumprisse o prazo, estaria sujeita à multa proporcional ao tempo de atraso. O setor de execução de obras da empresa verificou que, para cumprir o contrato, seriam necessários 20 operários com jornada diária de 6 horas. Seis meses após o início da obra, 5 operários foram demitidos, e a Construtora resolveu não contratar mais operários e concluir a obra com os restantes, aumentando a carga horária destes. Para cumprir o contrato, é CORRETO afirmar que a carga horária passou a ser de
A) 7 h/d
B) 8 h/d
C) 7h 20 h/d
D) 8h 30 h/d
E) 9 h/d
Solução:
Pelo planejamento da construtora, faltam dois meses para o término da obra. Veja que ela deseja terminar no mesmo prazo, porém com 15 e não 20 funcionários. Como o prazo é o mesmo, vamos analisar a quantidade de funcionários e a quantidade de h/d.
No primeiro caso, temos 20 funcionários trabalhando 6h/d, ou seja, 120 horas de trabalho por dia.
No segundo caso, temos 15 funcionários. Para que a obra termine também em 2 meses, precisamos que a carga horária diária também seja de 120 horas. Sendo x a quantidade de h/d, temos:
15.x = 120
x = 120/15
x = 8h/d
Resposta: B
35. A Polícia Militar de Pernambuco possui uma frota de 1500 carros, sendo que uma parte utiliza como combustível gasolina, e o restante, bicombustível, que funciona com álcool e gasolina. O novo comandante determinou que, neste total de 1500 carros, 80% dos carros a gasolina e 60% dos bicombustíveis sofressem uma conversão para também funcionar a gás. Sabendo que, após a conversão, 840 do total de carros passaram a utilizar dois e somente dois tipos de combustível, é CORRETO afirmar que o número de carros que permaneceram consumindo somente gasolina é igual a
A) 540
B) 620
C) 120
D) 400
E) 500
Solução:
G = número de carros a gasolina antes da conversão
A = número de carros bicombustíveis antes da conversão
Após a conversão:
O,8G passam a circular com gasolina e gás
0,4A continuam circulando a gasolina e álcool
Total de carros bicombustíveis:
0,8G + 0,4A = 840
Temos também que a frota é de 1500 carros:
G + A = 1500
A = 1500 – G
Substituindo na equação abaixo:
0,8G + 0,4A = 840
0,8G + 0,4(1500 – G) = 840
0,8G + 600 – 0,4G = 840
0,4G = 840 – 600
0,4G = 240
G = 240/0,4
G = 600
Daí, o número de carros a gasolina antes da conversão era de 600 veículos. Como 20% destes não foram convertidos, temos que 120 veículos permaneceram somente a gasolina.
Resposta: C
36. Um número é composto por dois algarismos. Sabendo que a soma do algarismo das dezenas com o algarismo das unidades é 8 e que, subtraindo o número do número formado, permutando-se o algarismo das unidades com o das dezenas, o resto dessa subtração é um número terminado em 6. É CORRETO afirmar que o produto dos algarismos das dezenas com o das unidades do número é
A) 40
B) 30
C) 45
D) 21
E) 12
Solução:
Seja xy o número de dois algarismos, onde x é o da dezena e y o da unidade.
Daí, pode ser escrito como 10x + y
Por exemplo, se o número fosse 27: 2.10 + 7
De “a soma do algarismo das dezenas com o algarismo das unidades é 8”, temos:
x + y = 8
De “subtraindo-se o número do número formado, permutando-se o algarismo das unidades com o das dezenas, o resto dessa subtração é um número terminado em 6”, temos:
xy – yx = 10x + y – 10y – x = __6
9x – 9y = __6
9(x – y) = __6
Como x e y são algarismos, temos que x – y < 10
Observando a tabuada de 9, x – y = 4, pois assim teríamos 9.4 = 36.
Temos então o sistema:
x + y = 8
x – y = 4
Somando:
x + y + x – y = 8 + 4
2x = 12
x = 6
Como x + y = 8 e x = 6, y = 2
Daí, o produto dos dois é 12.
Resposta: E
37. Três ciclistas A, B e C treinam em uma pista. Eles partem de um ponto P da pista e completam uma volta na pista ao passarem novamente pelo mesmo ponto P. O ciclista A gasta 30 seg , o ciclista B, 45 seg, e o ciclista C, 40 seg, para dar uma volta completa na pista. Após quanto tempo, os três ciclistas passam juntos, no ponto P, pela terceira vez consecutiva?
A) 18 min.
B) 25 min.
C) 30 min.
D) 15 min.
E) 20 min.
Solução
O encontro acontece em um múltiplo comum de 30, 45 e 40.
Como MMC( 30, 45, 40) = 360, o primeiro encontro ocorrerá com 360 segundos, o segundo encontro com 720 segundos e o terceiro encontro com 1080 segundos.
Transformando para minutos:
1080 seg / 60 = 18 min
Resposta: A
38. Uma livraria pretende fazer seu balanço anual. Pedro e João são os contabilistas da Empresa. Se os dois trabalhassem juntos no serviço, eles fariam o balanço em 6 dias, porém, se João trabalhar sozinho, realizará o serviço em 18 dias. Em quantos dias, Pedro, trabalhando sozinho, concluirá o balanço?
A) 15
B) 13
C) 9
D) 8
E) 20
Solução.
João, sozinho, demora 18 dias para fazer o balanço. Isto significa que ele faz 1/18 do balanço.
A questão fala que quando Pedro ajuda, o balanço é feito em 6 dias. A velocidade dos dois não muda, isso significa que quando eles trabalham juntos, João faz 1/3 do balanço:
6 dias x 1/18 = 1/3
Daí podemos concluir que Pedro faz 2/3 do balanço nos 6 dias, ou seja, a velocidade de Pedro é o dobro da velocidade de João. O que nos faz concluir que Pedro demora 9 dias, e não 18 dias como João.
Resposta: C
39. Uma loja de vendas de computadores fez uma parceria com determinada fábrica, para conceder um desconto de 20% na venda dessa marca. Um certo dia, foi vendido o último computador do estoque, porém a atendente vendeu o computador por R$ 1500,00, o que causou à loja um prejuízo de R$ 100,00. Sem a parceria, a loja venderia o computador por um preço cuja soma dos algarismos é igual a
A) 9
B) 13
C) 2
D) 19
E) 3
Solução
Preço da promoção 1600 (1500 + 100).
Sem o desconto de 20%, o preço seria:
0,8x = 1600
x = 1600/ 0,8
x = 2000
E a soma dos algarismos é igual a 2.
40. Resolvendo o sistema abaixo, é CORRETO afirmar que 2xy é igual a
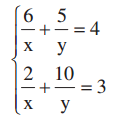
A) 12
B) 24
C) 16
D) 20
E) 18
Solução:
Para acabar com as frações e facilitar a nossa vida, vamos fazer as seguintes substituições:
u = 1/x e v = 1/y
Nosso sistema será:
6u + 5v = 4
2u + 10v = 3
Multiplicando a segunda equação por (-3):
6u + 5v = 4
-6u -30v = -9
Somando as equações:
-25v = -5
v = 1/5
Substituindo o valor de v:
6u + 5v = 4
6u + 1 = 4
6u = 4 – 1
6u = 3
u = 3/6 = 1/2
Como u e v são, respectivamente, o inverso de x e y, temos que x = 5 e y = 2.
Daí, 2xy = 2.5.2 = 20
