Boa noite caros candidatos a uma vaga na Polícia Militar do Estado de Pernambuco. Nesta página apresentaremos a prova resolvida do concurso da PM PE 2016, prova aplicada hoje pela UPENET.
A banca cobrou algumas questões bem interessantes sobre funções quadráticas e análise combinatória, porém deixou margem para algumas anulações. Das 10 questões de matemática, 3 são passíveis de anulação.
Boa sorte a todos!
Questão 26. Em uma campanha de doações à Creche Marias de Deus, feitas por um grupo de lojistas de uma pequena cidade, foram arrecadados 17 600 reais. Na reunião que decidiu quanto aos valores a serem doados por cada lojista, ficou acordado que a loja de menor lucro líquido anual doaria 800 reais, a segunda loja de menor lucro líquido anual, 400 reais a mais que a primeira, a terceira, 400 reais a mais que a segunda e assim sucessivamente.
Quantas lojas fizeram doação à Creche Marias de Deus?
A) 6
B) 9
C) 8
D) 10
E) 11
Resolução
A questão fala que foram arrecadados 17600 reais e todas as lojas doaram valores diferentes, sendo que a menor doou 800 reais, a segunda menor 1200, a terceira menor 1600…
Temos claramente uma Progressão Aritmética (PA), onde o primeiro termo é o 800, a razão é 400, e a soma dos termos é 17600. Precisamos descobrir a quantidade de termos.
Pela fórmula da soma de termos de uma PA:
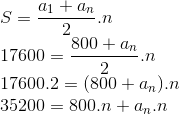
Pela fórmula do termo geral de uma PA:
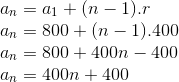
Substituindo o valor de an na primeira fórmula:
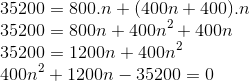
Podemos simplificar a equação do segundo grau, dividindo todos os termos por 400. Teremos:
n² + 3n – 88 = 0
Resolvendo a equação do segundo grau pelo método da soma e produto:
S = -b/a = -3/1 = -3
P = c/a = -88/1 = -88
Os dois números cuja soma é -3 e o produto é -88 são -11 e 8. Logo o conjunto solução é S = {-11, 8}.
Como buscamos o valor de n, que representa o número de lojas, n não pode ser negativo, daí temos que o número de lojas é 8.
Resposta: C
Questão 27. O ponto de interseção das curvas de oferta O e demanda D é chamado de “ponto de equilíbrio de mercado”. A abscissa desse ponto (preço de equilíbrio) é o preço de mercado para o qual a oferta é igual à demanda, ou seja, o preço para o qual não há escassez nem excesso do produto. Na figura abaixo, temos o esboço dos gráficos da função oferta O(x) = x² + x – 460 e da função demanda D(x) = 500 – x de certo produto, onde P é o ponto de
equilíbrio.
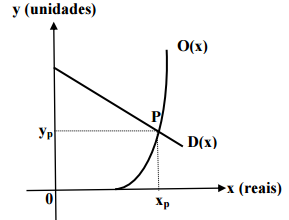
Qual é a demanda desse produto no mercado, quando ele estiver sendo oferecido pelo preço de equilíbrio?
A) 260 unidades
B) 310 unidades
C) 382 unidades
D) 470 unidades
E) 410 unidades
Resolução:
O ponto de equilíbrio ocorre quando as funções assumem os mesmos valores. Vamos descobri-lo:
x² + x – 460 = 500 – x
x² + x +x – 500 – 460 = 0
x² + 2x – 960 = 0
Resolvendo a equação do segundo grau pelo método da soma e produto:
S = -b/a = -2/1 = -2
P = c/a = -960/1 = -960
Os dois números cuja soma é -2 e o produto é -960 são -32, 30, daí o conjunto solução da equação é S = {-32, 30}.
Como o preço não pode ser negativo, temos que x = 30.
Agora basta utilizarmos qualquer das funções para calcularmos a demanda. Vamos utilizar a mais fácil:
D(30) = 500 – 30 = 470
Resposta: D
Questão 28. O domínio da função real f definida por f(x) = √(x-2) + √(2x-6) é o subconjunto dos reais, representado pelo intervalo
a) [0, +∞[
b) [2, +∞[
c) [1, +∞[
d) [5, +∞[
e) [3, +∞[
Resolução
Sabemos que não existe raiz real de um número negativo. Devemos então analisar os valores de x dentro dos radicais, de modo que:
No primeiro radical devemos ter x – 2 ≥ 0.
Daí, x ≥ 2.
No segundo radical devemos ter 2x – 6 ≥ 0.
Daí, 2x ≥ 6, e x ≥ 3.
Veja que x só pode assumir valores maiores ou iguais a 3, pois caso contrário, teremos uma raiz de um número negativo. Logo:
Domínio de f = [3, +∞[
Resposta: E
Questão 29. Antônio resolveu fazer duas pequenas aplicações em regime de juros compostos, num prazo de apenas um mês. Ele vai aplicar R$ 1 000,00, parte no Banco Alfa e parte no Banco Beta. Esses bancos cobram, respectivamente, uma taxa de 5% e 6% ao mês. Se Antônio resgatou o mesmo valor nas duas aplicações, quais os valores aproximados de investimento em cada banco?
A) R$ 392,00 e R$ 698,00
B) R$ 498,00 e R$ 502,00
C) R$ 474,00 e R$ 526,00
D) R$ 396,00 e R$ 604,00
E) R$ 520,00 e R$ 480,00
Resolução
Uma coisa é certa, para que o valor de resgate seja o mesmo, Antônio deve aplicar mais no banco que paga um juros menor. A única opção com essas características é a letra E, porém essa opção não está correta pois:
520,00 x 1,05 = 546,00
480,00 x 1.06 = 508,80
Percebe-se que não existe igualdade.
O gabarito oficial diz que a resposta correta é a letra B. Eu estava verificando algumas possibilidades de erro da banca e percebi que na verdade os valores estão trocados. Veja:
Se aplicarmos 5% sobre 502,00:
502,00 x 1,05 = 527,10
Se aplicarmos 6% sobre 498,00:
498,00 x 1,06 = 527,88
Resposta:. B, desde que a ordem seja trocada. Como a banca não utilizou a palavra respectivamente, acho difícil anular, mas quem errou vale a pena tentar.
30. Num batalhão da região metropolitana, 28% dos soldados são mulheres, e destas, 1,5% são residentes da cidade do Recife. Desse mesmo batalhão, 5% são homens que residem nessa mesma cidade. Qual é a probabilidade de um soldado desse batalhão, escolhido ao acaso, ser residente da cidade do Recife?
A) 1,18%
B) 4,02%
C) 3,50%
D) 2, 10%
E) 6, 98%
Resolução
Queremos a probabilidade de um soldado ser residente em Recife.
Temos que 28% são mulheres, e destas, 1,5% mora em Recife. Daí:
28% x 1,5% = 0,42%
Agora o ponto polêmico. Veja o que diz a questão: “Desse mesmo batalhão, 5% são homens que residem nessa mesma cidade”. A questão não fala que 5% dos homens são residentes em Recife, fala que 5% do batalhão é formado por homens que moram em Recife. Percebeu a diferença?
Temos então que a porcentagem total de residentes em Recife é de:
0,42% + 5% = 5,42%
Não existe essa opção, logo a questão deve ser anulada.
O erro da banca foi esse:
Como 28% do batalhão é formado por mulheres, é fácil concluir que os homens correspondem a 72%. A banca calculou 5% de 72%, que corresponde a 3,6%, que somados aos 0,42% das mulheres, da a resposta do gabarito.
Questão 31. Os batalhões que fazem parte da Diretoria Integrada Metropolitana da Polícia Militar (DIMPM) no Recife são os seguintes:
1º Batalhão da Polícia Militar
6º Batalhão da Polícia Militar
11º Batalhão da Polícia Militar
12º Batalhão da Polícia Militar
13º Batalhão da Polícia Militar
16º Batalhão da Polícia Militar
17º Batalhão da Polícia Militar
18º Batalhão da Polícia Militar
19º Batalhão da Polícia Militar
20º Batalhão da Polícia Militar
Se quatro batalhões foram selecionados ao acaso para indicar, cada um, oitenta militares para uma missão num país
asiático, por um período de seis meses, qual é a probabilidade de esse batalhão ser de ordem menor ou igual a 12?
A) 90%
B) 50%
C) 60%
D) 80%
E) 40%
Ao meu ver faltou alguma informação na questão pois ela pede “qual é a probabilidade de esse batalhão…”. Mas qual batalhão? Precisamos escolher 4.
Deve ser anulada por estar mal formulada.
Questão 32. Um foguete foi lançado de um ponto O do solo e descreveu uma trajetória em forma de parábola, até retornar ao solo. Se ele atingiu as alturas de y = 35m e y = 60m nos instantes x = 10s e x = 20s, respectivamente, qual foi a altura máxima alcançada por ele?
A) 40 m
B) 50 m
C) 60 m
D) 80 m
E) 70 m
Resolução
Se a trajetória do foguete foi em forma de parábola, podemos utilizar a função do segundo grau cujo gráfico é essa parábola.
Sabemos que uma função do segundo grau é da forma f(x) = ax² + bx + c.
Também sabemos 3 pontos dessa parábola: (0, 0), (10, 35) e (20, 60).
Vamos substituir esses valores para descobrirmos os valores de a, b e c:
Como a parábola corta o eixo y no ponto (0, 0), temos que c = 0, daí f(x) = ax² + bx
Substituindo os valores (10, 35):
35 = a.10² + b.10
35 = 100a + 10b
Substituindo os valores (20, 60):
60 = a.20² + b.20
60 = 400a + 20b
Basta resolvermos o sistema:
100a + 10b = 35
400a + 20b = 60
Multiplicando a primeira equação por -2:
-200a – 20b = -70
400a + 20b = 60
Somando as equações:
-200a – 20b + 400a + 20b = -70 + 60
200a = -10
a = -1/20
Substituindo na segunda equação:
400a + 20b = 60
400(-1/20) + 20b = 60
-20 + 20b = 60
20b = 60 + 20
20b = 80
b = 4
Daí, a função será f(x) = (-1/20).x² + 4x
Vamos calcular o instante onde a altura é máxima, que é o x do vértice da parábola:
xv = -b/2a
xv = -4/2(-1/20)
xv = 40
Veja que no instante 40 a altura é máxima.
Calculando a altura nesse instante:
f(x) = (-1/20).x² + 4x
f(40) = (-1/20).40² + 4.40
f(40) = -80 + 160
f(40) = 80
Daí, altura máxima é 80 m.
Resposta: D
Questão 33. Em certa cidade, a bandeirada comum numa corrida de táxi custa R$ 4,32. Na bandeira 1, o cliente paga R$ 2,10 por quilômetro rodado, e na bandeira 2, ele paga R$ 2,54. Se Carlos pagou R$ 65,28 por uma corrida na bandeira 2, qual foi a quilometragem de sua corrida?
A) 20 km
B) 26 km
C) 24 km
D) 28 km
E) 30 km
Resolução
A função afim que representa o custo em relação a quilometragem rodada na bandeira 2 é:
c(x) = 4,32 + 2,54.x
Como ele pagou 65,28:
65,28 = 4,32 + 2,54.x
65,28 – 4,32 = 2,54.x
2,54x = 60,96
x = 60,96/2,54
x = 24
Resposta: C
Questão 34. Num dia de chuva forte, foi identificada uma goteira no teto da sala de vídeo. Para controlar o pinga-pinga, a servente colocou uma pequena vasilha no chão, abaixo do local de onde as gotas caíam. Na primeira hora, a vasilha recebeu 5 gotas de chuva; na segunda hora, 25 gotas; na terceira, 125 gotas e assim por diante. Depois de quantas horas, essa vasilha recebeu 78 125 gotas?
A) 7
B) 6
C) 5
D) 8
E) 9
Resolução
Se fatorarmos o valor 78125, temos:
78125 = 5.5.5.5.5.5.5
Nota-se que o número primo 5 aparece 7 vezes, logo essa quantidade de gotas acontece após 7 horas.
Resposta: A
Questão 35. Um grupo de inquérito é formado por 8 oficiais e 4 soldados. Para analisar os processos, formam-se comissões com 4 oficiais e 2 soldados. Sendo A um oficial qualquer e B um soldado qualquer, qual é o número de comissões de que participa o oficial A e não participa o soldado B?
A) 105
B) 87
C) 64
D) 256
E) 504
Resolução
Para formarmos um grupo de 4 oficiais, onde o oficial A precisa estar, precisamos escolher os outros 3 entre 7 oficiais restantes. Temos uma combinação de 3 em 7:
C3,7 = 7!/3!.4! = 35
Para formarmos um par de 2 soldados, onde o soldado B não pode estar, precisamos escolher os 2 entre os outros 3 soldados restantes. Temos uma combinação de 2 em 3:
C2,3 = 3!/2!.1! = 3
O total será:
35 x 3 = 105
Resposta: A
Gostou da prova resolvida da PM PE 2016? Compartilhe nas redes sociais e deixe seu comentário aqui embaixo.
Boa sorte a todos e que Deus esteja com vocês!

Fiz essa prova e fui bem em todas menos matemática pois só acertei 3 questões será que umas dessas que o professor mencionou será anulada? pois com uma anulação em matemática livro o ponto de corte e ficou com 42 questões certas, será que existe essa possibilidade de ser alguma de matematica anulada?
Anderson, as questões 30 e 31 possuem uma boa chance de serem anuladas, principalmente a 30. A questão 29 está com a ordem trocada, dependendo da argumentação do recurso também tem chance.
Boa sorte!
Muito bom professor!!!’ Não sabia que a questão que abordava juros compostos, poderia ser possível de anulação. Já coloquei no meu recurso e enviei para a organização. Obg!
Olá Cláudio, tudo vai depender da banca. Ao meu ver inverter a ordem foi desnecessário.
Boa sorte!
Obrigado pela resolução. Muito boa.
Poderia comentar a prova de português pm pé 2016?
Desculpe Aline, mas eu sou professor apenas de Matemática rsrs
Boa sorte!
Como faço para mandar o formulário para recurso? Não estou conseguindo editá-lo.
Vc tem que imprimir depois de impresso VC preenche, depois e preenchido VC scaneia e envia
professor você acha que a banca usou de ma fê e foi maliciosa ao inverter os valores na questão 29 de juros composto induzindo o candidato ao erro?
Alexandre, achei desnecessário, mas acho difícil a banca ceder e anular a questão por esse motivo. O recurso terá que ser muito bem feito para ter chance.
Boa sorte!
Jordon, uma duvida. na questão 28 a resposta também não poderia ser a letra
D) [5, +∞[ ?: Já que x só pode assumir valores MAIORES ou iguais a 3, pois caso contrário, teremos uma raiz de um número negativo
Junior, a questão pede para identificarmos o domínio da função, e 4, por exemplo, pertence ao domínio. Por isso não pode ser a letra d.
Boa sorte!
Obrigado!
O problema pede o domínio para a função , porém o domínio é um subconjunto dos números reais que tornam 4 um número real. Isso ocorre na alternativa e na alternativa . Agora, se o problema pedisse o maior domínio, seria apenas a alternativa . Desta forma, solicito a anulação da questão devido a um erro no enunciado
Não procede?
Pessoal perdoe-me, mas como devo proceder no momento de recorrer, preencho no corpo do email ou envio o formulário anexo?
Olá, Jordon, com seria a argumentação, a respeito da questão 29? Sobre a ordem que foi trocada, se poder responder ficarei grato.
Paulo, você pode alegar que a palavra “respectivamente” foi utilizada no início da questão, causando dupla interpretação. Lembrando que a banca não gosta muito de anular questões.
Boa sorte!
A resposta certa para a questão 29, não consta das opçoes. Veja:
0,05x=0,06 y
x= 1,20 y
aí 1,20 + 1,00 = 2,20 logo: 1.000,00/2,20= 454,55
daí: 1.000,00 – 454,55 = 545,45
Fazendo a verificação: 545,45 x 1,06 = 27,27
454,55 x 1,05 = 27,27
Logo as aplicações foram 545,45 e 454,55.
A argumentação para anulação da questão 29 é a seguinte:
1,05 X – 1,06 Y
X=1,20 Y
CONSIDERANDO Y=1 E X= 1,20 X+Y=2,20
VALOR TOTAL R$ 1.000,00/2,20=454,54 VALOR INVESTIDO EM Y
R$ 1.000,00 – 454,54 = 545,46 VALOR INVESTIDO EM X
FAZENDO A VERIFICAÇÃO: 454,54 X 6% = 27,27
545,46 X 5% = 27,27
ABRAÇO
Gostaria tanto que questão 29 fosse cancelada, estou com pouca esperança
ELA DEVERIA SIM SER ANULADA. VEJA PORQUE:
0,05 X = 0,06 T
LOGO X = 1,20 Y
E Y = 1,00
X+Y=2,20
VALOR TOTAL A SER INVESTIDO = R$ 1.000,00/2,20 = 454,54 VALOR BANCO ALFA
DIFERENÇA BANCO BETA 545,46 VALOR BANCO BETA
FAZENDO A VERIFICAÇÃO: 454,54 X 6% =27,27
545,46 X 5% =27,27
LOGO NÃO HA ESSAS OPÇÕES NO GABARITO.
professor na questão 29 tem a palavra respetivamente .
Professor, bom dia. Sou aluno de Engenharia elétrica da universidade do Estado de Pernambuco, e sinceramente não vejo nehi questão passível de anulação, principalmente aquela dos batalhões, pois ele fala menor ou igual a 12, assim não precisa especificar qual batalhão.
A dos soldados que reside em recife, ele fala claramente. Os soldados residem na mesma cidade. Enfim, fico grato pelas revoluções, mas a prova estava sim difícil, porém todas as questões tem solução lógica.
Professor, você fala que na questão de juros composto que a banca não usa a palavra ”respectivamente” porém a questão traz essa palavra e deixando bem claro a ordem das aplicações. Assim acredito que a questão deve ser anulada.
Pessoal, quanto à prova de direito, creio que cabe recurso a questão 44 (prova verde)! “Sobre os direitos e garantias fundamentais, analise as alternativas abaixo: 1. As violações…” Nessa questão, o item 2 está marcado no gabarito como CORRETO, porém não existe hierarquia entre os direitos fundamentais previstos na Constituição Federal. O contrario do que diz a questão.
Bom Miguel essa questão não será anulada apenas foi marcada de forma errada no gabarito da prova verde, a resposta correta é a letra D.
Professor a questão que fala dos 4 batalhões ,VC acha possível anular?
Carla, essa questão está mal formulada. Espero que a banca anule sim.
Boa sorte!
Pessoal gostaria de saber se existe alguma possibilidade de alguma questão de história ser anulada? Prof Jordan em relação a questão de matemática que fala sobre o taxista, essa expressão Bandeirada,o Sr acha que nós não somos obrigados a saber como funciona? E a upenet podia sim colocar essa questão,porém melhorando mais a redação.o que o Sr acha?é possível entrar com recurso?
Jacqueline, acho difícil anularem a questão com esse argumento.
Boa sorte!
. Depois de quantas horas, essa vasilha recebeu 78 125 gotas?
Acho que essa pode ser anulada.
Em, na primeira hora, a vasilha recebeu 5 gotas de chuva; na segunda hora, 25 gotas; na terceira, 125 gotas. Até o terceiro dia a vasilha já recebeu 155 gotas. Na sexta hora receberá mais 78125 gotas.
O enuciado correto deveria ser: em uma hora, a vasilha recebeu 5 gotas de chuva; em duas hora, 25 gotas; em três , 125 gotas. Percebam a diferença.
Corrigindo meu erro …Até a terceira hora* a vasilha já recebeu 155 gotas. Na sexta hora receberá mais 78125 gotas.
O enuciado correto deveria ser: em uma hora, a vasilha recebeu 5 gotas de chuva; em duas hora, 25 gotas; em três , 125 gotas. Percebam a diferença. Hehe,
Obs: o (na) específica quantas gotas de chuva a vasilha receubeu naquela determinada hora e para o total de gotas dá a ideia de soma das gotas por cada hora. Essa questão deveria ser resolvida da mesma forma que a questão de PA desta prava. porém sendo PG
O (em) não específica. Daria a ideia continuidadeda PG. Ex: em 1h recebeu 5 gotas; em 2h, 25gotas; em 3h, 125 gotas. Fica fácil ver que na terceira hora a vasilha recebeu 125 gotas e que na sétima hora recebeu 78125 gotas.Diferente do (na) usado na questão.
Deveria ter a opção editar. Hehe
Outro erro do meu primeiro argumeto.
… na sétima hora a vasilha receberá MAIS 78125 gotas.
Mesmo com outros erros existentes acho que já consegui passar a minha opinião. E espero que o professor me entenda e me responda se estou certo ou errado. Pra mim estou 100% certo, mas nunca se sabe né.
Olá David,
Eu entendi seu argumento mas não cabe na questão. A redação utilizada deixa claro que não devemos somar as gotas.
Boa sorte!
Obrigado. Pingos constantes, invariável . Hehe percebi essa ideia tabem. Pra mim ficou uma questão ambígua. Mas obrigado pelo esclarecimento.
Ignore o que foi dito anteriormente. Mas olhando com mais atenção fico com minha primeira opinião.
Gostaria que se possível o professor me mostrasse em qual parte da redação fica claro que não se deve somar ,alguma sentença.
Professor, acertei apenas duas e fui ótima em todas as outras. Gostaria de saber sobre a questão 31 e 29, o senhor mandou recursos? estou confiando nas anulações para passar em matemática 🙁
Rayane, não mandei nenhum recurso, fiz as resoluções e deixei a cargo dos candidatos.
Boa sorte!
Professor na opinião do senhor,será que pelo menos uma dessas de matemática que o senhor mencionou tem possibilidade de ser anulada?
Professor será que o Sr. tem como dar uma dica de redigir o texto de argumentação do recurso sobre a questão de matemática. Especificamente a dos “5% dos soldados de recife”? Obrigado.
Wagner, acho que você poderia pegar o que escrevi sobre a questão. Os argumentos utilizados comprovam que a questão está errada.
Boa sorte!
Boa noite! Estou na mesma situação da Reyane, fiz uma boa pontuação nas outras disciplinas, porém só acertei duas de matemática. Com quantas questões anuladas terei chance de aprovar nessa disciplina?
Olá!
No meu entendimento existem 3 com possibilidade. Espero que a banca tenha bom senso e anule pelo menos as questões 30 e 31.
Boa sorte!
Obrigada!
Acho que a pergunta da questão 34 deveria ser:
Em que hora a vasilha receberá 78125 gotas? Ou
Em qual hora a vasilha receberá 78125 gotas? Ou algo desse tipo. Menos em quantas como foi usado na questão.
“Em quantas”
Parabéns pelo site
ótimo
Jordan, tudo bem? Professor eu até entendo que a questão 30 seja anulada, agora a 31 que foi anulada cheira a trambicagem para beneficiar algum parente ou amigo de políticos, o que não é surpresa em nosso país. De qual batalhão?
Quando ele pergunta “a probabilidade de esse batalhão”, ele se refere ao batalhão que for sorteado. Qual batalhão? O que for sorteado ao acaso. lógico não?
Olá Silvio!
Realmente a questão foi mal formulada, penso eu que devido a um erro de digitação.
Olá professor, queria tirar uma dúvida. Por que na questão de juros o senhor multiplicou os valores por 1,05 e 1,06?
Olá Klainn!
Quando queremos aumentar em 5%, multiplicamos por 1,05.
Da mesma forma, quando queremos aumentar em 6%, multiplicamos por 1,06.
não estou conseguindo aprender essas partes, poderia indicar algum link que explique essa parte de sistemas?
Questão 32.
Basta resolvermos o sistema:
100a + 10b = 35
400a + 20b = 60
Multiplicando a primeira equação por -2:
-200a – 20b = -70
400a + 20b = 60
Somando as equações:
-200a – 20b + 400a + 20b = -70 + 60
200a = -10
a = -1/20
https://sabermatematica.com.br/sistemas1graumd.html