Estudando matemática para concursos? Confira aqui a prova resolvida do concurso para a Polícia Militar do Maranhão (PM MA), realizado em 2012 pela FGV.

Não deixe de ver as nossas provas resolvidas referente a outros concursos de carreiras policiais.

Boa sorte!

 

 

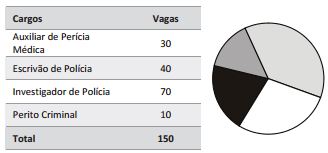
Questão 21. Em certo estado, a Polícia Civil está realizando um concurso para  preenchimento  de  150  vagas  para  os  cargos  que  estão na tabela a seguir.

 

Para visualizar a relação entre os números de vagas, foi feito um gráfico de setores. Nesse gráfico, o ângulo central de cada setor é proporcional ao número de vagas do cargo correspondente. O ângulo central do setor correspondente ao cargo de escrivão de polícia será de

(A) 40º

(B) 72º

(C) 80º

(D) 96º

(E) 128º

 

Resolução

Para resolvermos a questão, basta recordarmos que o ângulo que representa uma volta completa, ou seja, a soma de todos os ângulos centrais é de 360 graus.

Assim, 150 vagas corresponde a 360 graus. Precisamos calcular qual o ângulo que corresponde as 40 vagas de escrivão.

Podemos resolver utilizando “regra de três”:

150x = 40.360

150x = 14400

x = 14400/150

x = 96º

 

Resposta: D

 

 

Questão 22. Na delegacia de certo bairro os policiais Abel, Bento, Cléber e Danilo estão escalados para trabalhar no dia 31 de dezembro deste ano. Entretanto, dois deles serão sorteados para trabalhar na noite do Ano Novo. A probabilidade de que Abel não seja sorteado é

(A) 25%.

(B) 40%.

(C) 50%.

(D) 60%.

(E) 75%.

 

Resolução

Vamos simular o sorteio:

No primeiro sorteio, Abel tem 3/4 (é sorteado 1 em 4) de chances de não ser sorteado para trabalhar.

No segundo sorteio, Abel tem 2/3 (é sorteado 1 em 3) de chances de não ser sorteado para trabalhar.

 

3/4 x 2/3 = 2/4 = 0,5 = 50%

Resposta: C

 

 

Questão 23. Dados os vetores u = (3, 1)  e  v = (–1, 1)  o módulo do vetor 3u + v é aproximadamente igual a

(A) 8.

(B) 9.

(C) 10.

(D) 11.

(E) 12.

 

Resolução

3u + v = 3(3, 1) + (-1, 1) = (9, 3) + (-1, 1) = (8, 4)

 

Calculando o módulo de (8, 4):

√(8² + 4²) = √(64 + 16) = √80

 

A questão quer o valor aproximado, logo a resposta é 9, pois √81 = 9

Resposta: B

 

 

Questão 24. Cinco soldados possuem alturas diferentes e devem formar uma fila. O  capitão diz que o mais alto e o mais baixo dos soldados não podem ocupar os extremos da fila, ou seja, nenhum dos dois pode ser nem o primeiro nem o último da fila. O número de maneiras diferentes que essa fila pode ser organizada é:

(A)  12.

(B)  18.

(C)  24.

(D)  36.

(E)  48.

 

Resolução

Temos 5 pessoas.

O mais baixo e o mais alto não podem ocupar os extremos da fila.

 

Vamos organizar a fila:

Quantos podem ficar na primeira posição?

3 (exceto o mais alto e o mais baixo)

Quantos podem ficar na última posição?

2 (exceto o mais alto, o mais baixo e o que ficou na primeira posição)

Quantos podem ficar na segunda posição?

3 (os três que sobraram)

Quantos podem ficar na terceira posição?

2 (os dois que sobraram)

Quantos podem ficar na quarta posição?

1 (o que sobrou)

 

Quantidade de maneiras:

3 x 2 x 3 x 2 x 1 = 36

Resposta: D

 

 

Questão 25. Na circunferência trigonométrica o arco x é tal que sen(x) = 1. Então, cos(2x) é igual a:

(A)  –2.

(B)  –1.

(C)  0.

(D)  1.

(E)  2.

 

Resolução

Na circunferência trigonométrica, o ângulo cujo seno é 1 é 90 graus.

Então, cos(2x) = cos(180) = -1

Resposta: B

 

 

Questão 26. A reta r passa pelos pontos ( –1, 1 ) e ( 2, 3 ). Entre os pontos abaixo, o único que pertence à reta r é:

(A)  (30, 21).

(B)  (31, 22).

(C)  (32, 23).

(D)  (33, 24).

(E)  (34, 25).

 

Resolução

Três pontos estão alinhados quando as diferenças entre suas coordenadas estão na mesma proporção.

Veja:

(2, 3) – (-1, 1) = (3, 2)

Veja que a variação de x sobre a variação de y está na razão 3/2.

 

Verificando os pontos (2, 3) e (32, 23):

(32, 23) – (2, 3) = (30, 20)

 

Como 30/20 = 3/2, a resposta é a letra C pois as outras opções não apresentam essa mesma proporção.

Resposta: C

 

 

Questão 27. Cinco pessoas, Luiz, Mário, Nilton, Otávio e Pedro trabalham juntos e possuem  idades diferentes. Luiz, Otávio e Pedro sabem as idades de todos e fazem as seguintes afirmações:

•    Luiz diz que é mais novo que Nilton e mais velho que Otávio.

•    Pedro diz que só há uma pessoa mais velha que ele.

•    Otávio diz que ele não é o mais novo.

Organizando uma fila com essas pessoas em ordem crescente de idade, ou seja, a primeira é a mais nova e a última a mais velha, pode-se concluir que:

(A)  Otávio é o terceiro da fila.

(B)  Pedro está na frente de Luiz.

(C)  Luiz não é o terceiro da fila.

(D) Mário é o segundo da fila.

(E)  Nilton é o último da fila.

 

Pela afirmação de Luiz:

N > L > O

 

Como Otávio não é o mais novo, deve ser Pedro ou Mário, mas só tem uma pessoa mais velha que Pedro, logo o mais novo é Mário, e Pedro está entre  Nilton e Luiz:

N > P > L > O > M

 

Resposta: E

 

 

Questão 28. Para  tornar  uma  mensagem  secreta,  uma  palavra  foi codificada de acordo com as instruções a seguir:

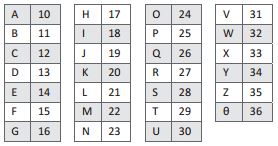
I.  Você deve substituir cada letra pelo número correspondente da tabela a seguir:

II.  Se o número for múltiplo de 3, você deve subtrair duas unidades dele. Se não for, some uma unidade a ele;

III.  Substitua cada novo número pela letra correspondente.

Por  exemplo,  a  palavra  PAULO  corresponde  à  sequência  25-10-30-21-24,  que  após  ser  modificada  será  26-11-28-19-22, formando a palavra codificada QBSJM.

A palavra EGJBO está codificada. Decodificando-a, você obtém

(A)  DILAN.

(B)  DENIS.

(C)  CELSO.

(D)  FHKCM.

(E)  DFKCO.

 

Resolução

Vamos fazer o inverso:

EGJBO corresponde a 14-16-19-11-24

 

Se o número é do tipo múltiplo de três mais um, então ele era múltiplo de 3 e foram subtraídas duas unidades

Se o número for múltiplo de três ou do tipo múltiplo de três mais dois, então foi somada uma unidade.

 

14 = 3.4 + 2, logo o número era 13

16 = 3.5 + 1, logo o número era 18

19 = 3.6 + 1, logo o número era 21

11 = 3.3 + 2, logo o número era 10

24 = 3.8, logo o número era 23

 

13-18-21-10-23 corresponde a DILAN

Resposta: A

 

 

Questão 29.  Um pai propõe um jogo ao filho:

“Vou lançar esta moeda três vezes. Cada vez que der cara você ganha 3 reais e cada vez que der coroa você perde 2 reais”.

A probabilidade que o filho tem de ganhar 4 reais é:

(A)  1/8.

(B)  1/4.

(C)  1/3.

(D)  3/8.

(E)  1/2.

 

Resolução

Temos duas opções em cada uma das três jogadas. Logo, o número de opções será 2.2.2 = 8.

 

O filho só ganha 4 reais é se saírem duas caras e uma coroa. Temos três opções para isso ocorrer:

Cara-Cara-Coroa

Cara-Coroa-Cara

Coroa-Cara-Cara

 

A probabilidade será de 3/8

Resposta: D

 

 

Questão 30. Lucas é  vigia noturno de uma empresa e deve escolher os três dias em que  trabalhará na próxima  semana. Para  fazer isso ele deve preencher uma ficha como a apresentada a seguir.

O número de maneiras diferentes que Lucas pode preencher essa ficha é:

(A)  35.

(B)  70.

(C)  105.

(D)  210.

(E)  343.

 

Lucas deve escolher 3 em 7 dias.

Trata-se de uma combinação simples de 3 em 7:

C(3,7) = 7! / 3!.4! = 7.6.5/3.2.1 = 35

Resposta: A

 

 

Gostou da prova resolvida do concurso da PM do Maranhão (2012)?

Deixe o seu comentário.