Confira aqui a prova resolvida do concurso para a Polícia Militar do Estado de Alagoas (PM AL), realizado em 2021 pelo CESPE, para o cargo de soldado.
Cada um dos próximos itens apresenta uma situação hipotética seguida de uma assertiva, a ser julgada com base na matemática e em suas aplicações na atividade policial.
39. Um fugitivo tenta despistar policiais, realizando uma fuga entre três cidades (A, B e C). Existem duas estradas ligando a cidade A à B e três estradas ligando a cidade B à C. Nessa situação hipotética, há 12 formas diferentes de o fugitivo ir da cidade A até a C, passando pela cidade B, voltando para a cidade A e passando novamente pela cidade B, sem repetir as estradas que usar para ir de A a C.
Resolução
Observe na figura abaixo que existem dois caminhos entre as cidades A e B, e três caminhos entre B e C.
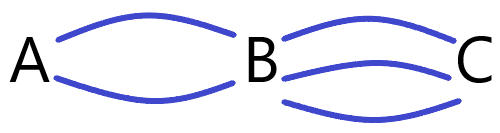
O fugitivo deverá efetuar o seguinte trajeto:
Ida:
A → B: 2 opções
B → C: 3 opções
C → B: 2 opções, pois ele não poderá repetir as estradas
B → A: 1 opção, pois ele não poderá repetir as estradas
Total de possibilidades:
2 x 3 x 2 x 1 = 12
Resposta: CERTO
40. Em uma cidade, existem três antenas de celular — A, B e C —, representadas em um plano cartesiano de tal forma que A(0, 0), B(2, 0) e C(1/2, √3/2), em que as unidades estão em quilômetros. As antenas A e B captam um telefone celular que está em um ponto P(x0, y0) localizado a 2 km de distância de cada uma delas, e a antena C também recebe sinal desse aparelho. Nesse caso, sabendo-se que y0 > 0, conclui-se que a distância entre P e C é igual a 1 km.
Resolução
As localizações das três antenas (A, B e C) podem ser representadas em um plano cartesiano.Observe que o telefone celular está em um ponto P, localizado a 2 km de A e B, e como y0 > 0, a figura ABP possui o formato de um triângulo equilátero.
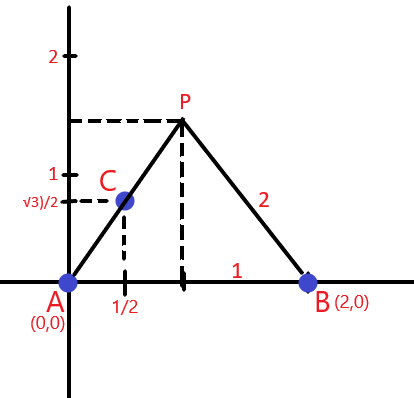
Utilizaremos o Teorema de Pitágoras para calcular a altura h de ABP:
2² = h² + 1²
4 = h² + 1
h² = 4 – 1
h = √3
Observe que A(0,0), C(1/2, √3/2), P(1, √3) são colineares, ou seja, podemos calcular a distância PC através do Teorema de Pitágoras:
PC² = (√3/2)² + (1/2)²
PC² = 3/4 + 1/4
PC² = 4/4
PC² = 1
PC = 1
Resposta: CERTO
41. Um corpo com temperatura inicial de 36 °C está em um ambiente cuja temperatura é de 20 °C. Nesse ambiente, vão demorar 20 minutos para que a temperatura inicial do corpo caia para 28 °C. Sabendo-se que o resfriamento de um corpo pode ser modelado pela lei do resfriamento de Newton, conforme a qual a temperatura do corpo T, em função do tempo t, em horas, é dada pela função exponencial T(t) = (Tc−Ta)10-kt + Ta, em que Tc é a temperatura inicial do corpo e Ta é a temperatura ambiente, é correto afirmar que a constante k é igual a log10(27).
Resolução
Considerando que 20 minutos é 1/3 de uma hora, podemos utilizar a função exponencial:
T(t) = (Tc − Ta)10-kt + Ta
28 = (36 − 20)10-k/3 + 20
28 – 20 = 16.10-k/3
8 = 16.10-k/3
10-k/3 = 8/16
10-k/3 = 1/2
Aplicando log em ambos os lados da igualdade:
log(10-k/3) = log(1/2)
(-k/3).log10 = log1 – log2
(-k/3).1 = 0 – log2
k/3 = log2
k = 3log2
Resposta: ERRADO
42. Ao analisar a média aritmética de ocorrências criminais anuais de uma região, um policial verificou que, nos 10 primeiros meses do ano, a média havia sido de 315 ocorrências por mês, contudo a média para o ano todo era 10% maior que a média dos 10 primeiros meses. Nessa situação hipotética, a média aritmética de ocorrências apenas nos dois últimos meses do ano é superior a 500 ocorrências por mês.
Resolução
Considerando que a média dos 10 primeiros meses é igual a 315 ocorrências, podemos concluir que neste período tivemos:
10 x 315 = 3150 ocorrências.
Considerando que a média para o ano todo era 10% maior que a média dos 10 primeiros meses, podemos concluir que a média foi de:
315 + 31,5 = 346,5
Considerando que x representa o total de ocorrências nos dois últimos meses do ano, a média referente aos 12 meses é dada por:
(3150 + x)/12 = 346,5
3150 + x = 346,5 . 12
3150 + x = 4158
x = 4158 – 3150
x = 1008
Como a soma dos dois últimos meses é igual a 1008, a média desses meses é dada por:
1008 / 2 = 504
Resposta: CERTO
Com relação às geometrias plana, espacial e analítica, julgue os itens que se seguem.
43. A soma dos ângulos internos de um heptágono regular é 720°.
Resolução
O heptágono regular é um polígono que possui 7 lados iguais.
Podemos calcular a soma dos ângulos internos deste tipo de figura através da seguinte fórmula:
Sn = (n – 2).180°
S7 = (7 – 2).180°
S7 = 5 . 180°
S7 = 900°
Resposta: ERRADO
44. Sendo ABC um triângulo, em que  = 45°, B̂ = 60° e AB = 1, então a altura h relativa ao vértice C tem comprimento dado por h = (3 – √3)/2
Resolução
Traçando a altura h relativa ao vértice C, o triângulo ABC será dividido em outros dois triângulos ADC e DBC.
Considere que AD = x e que DB = 1 – x.
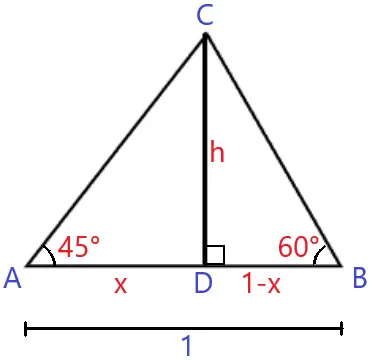
– Triângulo ADC
tg45° = h/x
1 = h/x
x = h
– Triângulo DBC
Tg60° = h/(1-x)
√3 = h/(1-x)
√3.(1-x) = h
√3 – x√3 = h
Como x = h, temos que:
√3 – x√3 = h
√3 – h√3 = h
h + h√3 = √3
h(1 + √3) = √3
h = √3/(1 + √3)
Racionalizando:
h = √3 . (1 – √3) / (1 + √3) . (1 – √3)
h = (√3 – 3) / (1 – 3)
h = (3 – √3)/2
Resposta: CERTO
45. A área superficial de uma pirâmide de base quadrada regular em que todas as arestas são iguais a 2 é S = 4 + 4√3.
Resolução
A figura abaixo apresenta uma pirâmide de base quadrada regular com as dimensões informadas.
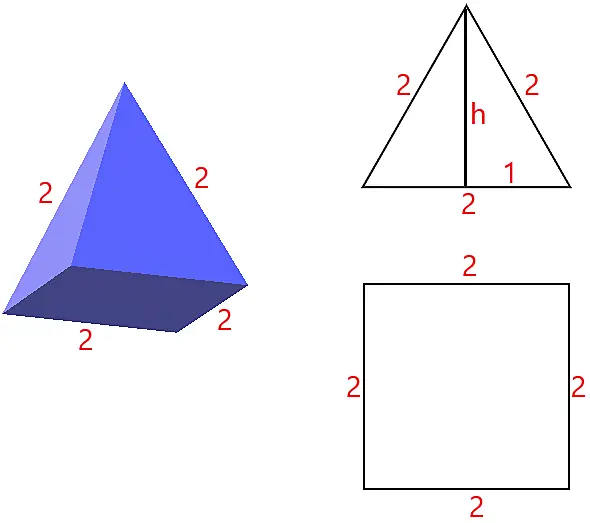
Observe que a pirâmide apresenta 4 faces de formato triangular e uma face no formato de um quadrado.
Calcularemos a altura, utilizando o Teorema de Pitágoras, e em seguida a área do triângulo.
Calculando a altura do triângulo
2² = h² + 1²
4 = h² + 1
h² = 4 – 1
h = √3
Calculando a área do triângulo
A = √3.2/2 = √3
Calculando a área do quadrado
A = 2 x 2 = 4
Consideramos que temos 4 triângulos e um quadrado, é possível calcular a área superficial da pirâmide:
4 x √3 + 4 = 4 + 4√3
Resposta: CERTO
46. Dados os números complexos z = x + iy e z0 = 2 − i, em que i é a unidade imaginária, é correto afirmar que |z − z0| = 2 representa, no plano complexo, uma circunferência de raio √2 com centro no ponto z0.
Resolução
|z − z0| = 2
| (x + iy) – (2 – i) | = 2
| x + iy – 2 + i | = 2
| (x – 2) + (y + 1)i | = 2
Calculando o valor do módulo:
√[ (x – 2)² + (y + 1)² ] = 2
(x – 2)² + (y + 1)² = 2²
Observe que |z − z0| = 2 representa uma circunferência de raio 2, com centro em (2, -1), ou seja, está centralizada em z0, porém possui raio 2 e não √2.
Resposta: ERRADO
Julgue os itens a seguir, relacionados a álgebra e aritmética.
47. O resto da divisão do polinômio p(x) = 4x³ – 2x² – 3 pelo polinômio q(x) = 2x² – 1 é r(x) = 3x – 3.
Resolução
Efetuando a divisão de polinômios, temos que:
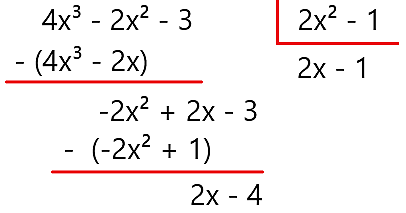
Resposta: ERRADO
48. O maior valor da função trigonométrica f(x) = sen²(x) − 4sen(x) + 5 é 10.
Resolução
Observe que sen(x) pode assumir apenas valores entre -1 e 1.
Analisando cada parte da função dada, temos que:
O valor máximo de sen²(x) é 1, quando sen(x) = -1 ou sen(x) = 1.
O valor máximo de −4sen(x) é 4, quando sen(x) = -1
Considerando sen(x) = -1, temos:
sen²(x) − 4sen(x) + 5 = 1 + 4 + 5 = 10
Resposta: CERTO
49. Se a soma dos seis primeiros termos de uma progressão aritmética de razão 2 é 48, então o 5.º termo dessa progressão é 13.
Resolução
Considere uma progressão aritmética de razão 2, com 6 termos, e cuja soma dos termos seja igual a 48.
a1 = ?
r = 2
a6 = ?
S6 = 48
Pela fórmula do termo geral:
an = a1 + (n – 1)r
a6 = a1 + (6 – 1).2
a6 = a1 + 10
a1 = a6 – 10
Pela fórmula da soma dos termos:
Sn = (a1 + an).n/2
S6 = (a1 + a6).6/2
48 = (a1 + a6).3
a1 + a6 = 16
a1 = 16 – a6
Considerando que a1 = a6 – 10:
a1 = 16 – a6
a6 – 10 = 16 – a6
a6 + a6 = 16 + 10
2a6 = 26
a6 = 26/2
a6 = 13
Como a6 = 13 e r = 2:
a5 = a6 – r
a5 = 13 – 2
a5 = 11
Resposta: ERRADO
50. Considerando-se que, em uma loja, 2 mesas e 3 cadeiras, juntas, custem R$ 1.350 e 3 mesas e 2 cadeiras custem R$ 1.650, é correto afirmar que, nessa loja, o custo de uma cadeira e uma mesa é R$ 500.
Resolução
Considere que:
M = custo de uma mesa
C = custo de uma cadeira
“2 mesas e 3 cadeiras, juntas, custem R$ 1.350”
2M + 3C = 1350
“3 mesas e 2 cadeiras custem R$ 1.650”
3M + 2C = 1650
Somando as duas equações:
2M + 3C + 3M + 2C = 1350 + 1650
5M + 5C = 3000
5(M + C) = 3000
M + C = 3000/5
M + C = 600
Resposta: ERRADO
Gostou da prova resolvida do concurso para a Polícia Militar do Estado de Alagoas (PM AL 2021)?
Deixe o seu comentário.
