Confira aqui a prova resolvida do concurso da Polícia Militar do Estado do Acre (PM AC), realizado em 2017 pelo IBADE – INSTITUTO BRASILEIRO DE APOIO E DESENVOLVIMENTO EXECUTIVO.
Não deixe de ver também nossas outras provas resolvidas de concursos de carreiras policiais.
Boa sorte!
Questão 26. Sabe-se que P = {p ∈ R | p é divisor de 180}, Q = {q ∈ Z+ | q < 30} e k é o número de elementos do conjunto P – Q. Dessa forma, k vale:
a) 4
b) 6
c) 2
d) 5
e) 3
Questão ANULADA pela banca.
Questão 27. Duas patrulhas A e B, de um mesmo Batalhão de Polícia Militar fazem ronda em diferentes bairros da cidade. A patrulha A efetua a ronda no bairro da Sorte e, caso não atenda a nenhuma ocorrência, retorna ao Batalhão em exatos 35 minutos, saindo em seguida para a próxima ronda. A patrulha B efetua a ronda no Bairro Esperança e, não atendendo a nenhuma ocorrência, retorna ao Batalhão em exatos 40 minutos, saindo em seguida para a próxima ronda.
Considerando que, no último domingo, as duas patrulhas saíram juntas do Batalhão às 14 horas e 50 minutos, se não houve ocorrências para ambas, em que horário elas voltaram a se encontrar no Batalhão?
a) 18h e 55min
b) 19h e 25min
c) 18h e 50min
d) 19h e 30min
e) 18h e 20min
Resolução
A patrulha A retorna a cada 35 minutos, enquanto a patrulha B retorna a cada 40 minutos.
Como não existiram ocorrências, basta calcularmos o MMC de 35 e 40.
Temos:
35 = 5.7
40 = 2³.5
Daí, MMC(35, 40) = 280, ou seja, as patrulhas se encontrarão a cada 280 minutos, que equivale a 4 horas e 40 minutos.
Como as patrulhas saíram juntas às 14:50, podemos concluir que se encontrarão às 19:30.
Resposta: D
Questão 28. A febre amarela é uma doença infecciosa aguda, de curta duração (no máximo 10 dias), gravidade variável, causada pelo vírus da febre amarela, que ocorre na América do Sul e na África. A única forma de evitar a febre amarela silvestre é a vacinação contra a doença. A vacina é gratuita e está disponível nos postos de saúde em qualquer época do ano.
Um posto de saúde iniciou a vacinação contra a febre amarela com um lote de x doses. Sabe-se que o planejado é que o número de doses produzidas dobre a cada ano. Dessa maneira, após quanto tempo esse número passará a ser igual a 20 vezes o inicial? (Use: log2 = 0,3).
a) 4 anos e 4 meses
b) 10 anos e 3 meses
c) 3 anos e 4 meses
d) 4 anos e 1 mês
e) 13 anos e 3 meses
Resolução
Sendo x a quantidade inicial de doses e considerando que o número deve dobrar a cada ano, podemos montar a equação abaixo, onde n é a quantidade de anos.
2n.x = 20.x
2n = 20
log(2n) = log20
n.log2 = log2 + log10
n.0,3 = 0,3 + 1
0,3n = 1,3
n = 1,3/0,3
n = 4,33…
n = 4 anos e 4 meses
Resposta: A
Questão 29. Doze policiais militares foram mapeados de acordo com o rendimento em 90 dias. Trabalhando todos eles, durante 8 horas por dia, verificou-se que eles conseguiram produzir 288 páginas de um relatório sobre criminalidade local. Sendo assim, em quantos dias de 6 horas trabalhadas, 15 policiais militares produzirão 192 páginas desse mesmo relatório?
a) 48
b) 72
c) 64
d) 36
e) 24
Resolução
Questão típica de regra de três composta.
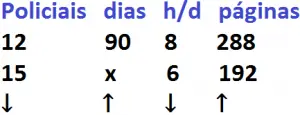
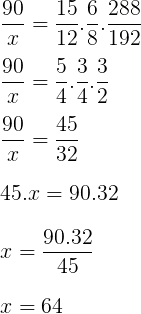
Resposta: C
Questão 30. Helaine está grávida e muito feliz com o seu primeiro bebê. Muito ansiosa em arrumar o quarto da criança, ela faz algumas estimativas, quanto as suas preferências em relação ao sexo e ainda da cor que irá pintar o quarto. Caso o exame detecte um menino, a probabilidade de ela pintar o quarto do bebê de azul é de 70% e de branco é de apenas 30%. Mas, se o exame detectar que é uma menina, a probabilidade de ela pintar o quarto do bebê de rosa é de 60% e de branco 40%.
Sabendo-se que a probabilidade de o exame detectar um menino é de 50%, a probabilidade de Helaine pintar o quarto do bebê de branco é de:
a) 40%
b) 55%
c) 20%
d) 35%
e) 70%
Resolução
Existe a possibilidade do quarto pode ser pintado de branco nos dois casos:
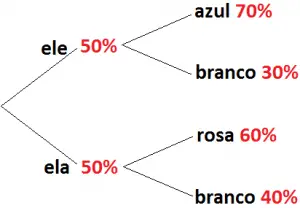
– Se nascer menino (50%), a probabilidade de pintar de branco é de 30%, ou seja, 15%;
– Se nascer menina (50%, a probabilidade de pintar de branco é de 40%, ou seja, 20%.
Total: 35%
Resposta: D
Questão 31. Sabe-se que o determinante da matriz M vale 2 e o determinante da matriz N vale 8. Se M e N são matrizes de ordem 2, o valor do det[(2.MT).(4.N-1)] é:
a) 2³
b) 2²
c) 2¹
d) 24
e) 20
Resolução
Sabendo que det(AB) = detA . detB, temos que:
det[(2.MT).(4.N-1)] = det(2.MT) . det(4.N-1)
Sabendo que det(k.A) = kn.detA, onde n é a ordem da matriz quadrada A, temos que:
det(2.MT) . det(4.N-1) = 2².det(MT) . 4².det(N-1) = 4.det(MT) . 16.det(N-1) = 64.det(MT).det(N-1)
Sabendo que det(AT) = detA, e det(A-1) = 1/detA, temos que:
64.det(MT).det(N-1) = 64 . detM . 1/detN
Como detM = 2 e detN = 8, temos que:
64 . detM . 1/detN = 64.2.1/8 = 16 = 24
Resposta: D
Questão 32. Considere que um triângulo retângulo escorrega, descendo sobre um plano inclinado ABC, retângulo em A. No momento em que ele assume a posição representada na figura, sabe-se que AC = 5dm e AB = CD = 12dm
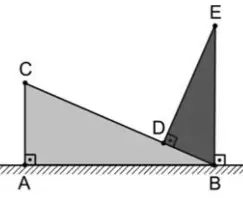
Se DE = x e BE = y, marque a alternativa que contém o correto valor, em decímetros, de x + y.
a) 17/5
b) 23/5
c) 5
d) 4
e) 3
Resolução
O primeiro passo é localizar na figura as medidas informadas pelo enunciado da questão.
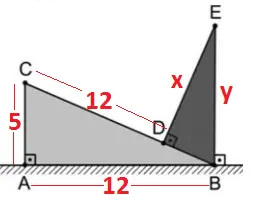
Calculando a medida de CB através do Teorema de Pitágoras:
CB² = AC² + AB²
CB² = 5² + 12²
CB² = 25 + 144
CB² = 169
CB = 13
Como CB = 13 e CD = 12, podemos concluir que BD = 1.
É possível observar na figura que temos dois ângulos complementares nos vértices B, de onde podemos concluir que os triângulos ABC e DEB são semelhantes. Calculando os valores de x e y:
AB/AC = DE/BD
12/5 = x/1
x = 12/5
CB/AC = EB/BD
13/5 = y/1
y = 13/5
x + y = 12/5 + 13/5 = 25/5 = 5dm
Resposta: C
Gostou da nossa prova resolvida do concurso para a Polícia Militar do Estado do Acre (PM AC) realizado em 2017?
Deixe o seu comentário e compartilhe nas redes sociais.

Professor essa questão 30. Não entendi.
Olá Lucas!
Qual é a sua dúvida?
simplesmente muito bom