Confira aqui a prova resolvida do concurso para a Polícia Federal (PF), realizado em 2018 pelo Cespe.
Lembrando que você encontra várias provas resolvidas de carreiras policiais em nosso menu.
Boa sorte!
As proposições P, Q e R a seguir referem-se a um ilícito penal envolvendo João, Carlos, Paulo e Maria.
P: “João e Carlos não são culpados”.
Q: “Paulo não é mentiroso”.
R: “Maria é inocente”.
Considerando que ~X representa a negação da proposição X, julgue os itens a seguir.
Questão 51. Se as três proposições P, Q e R forem falsas, então pelo menos duas das pessoas envolvidas no ilícito penal serão culpadas.
Resolução
Assumindo que P, Q e R são falsas, podemos concluir que as negações ~P, ~Q e ~R são verdadeiras.
Temos:
~P: João é culpado ou Carlos é culpado (pelo menos um deles é culpado).
~Q: Paulo é mentiroso.
~R: Maria não é inocente (Maria é culpada).
Conclusão: Pelo menos duas pessoas são culpadas.
Resposta: Certo
Questão 52. As proposições P, Q e R são proposições simples.
Resolução
As proposições Q e R são claramente simples.
A grande dúvida aqui é em relação a proposição P.
O Cespe costuma considerar as proposições do tipo “João e Carlos não são culpados” como uma proposição simples, pelo fato de existir apenas uma oração. Já as proposições do tipo “João não é culpado e Carlos não é culpado”, onde existem duas orações, são consideradas pelo Cespe como proposição composta.
Eu não concordo com o posicionamento do Cespe, mas esta tem sido a linha de raciocínio.
Resposta: Errado
Questão 53. A proposição “Se Paulo é mentiroso, então Maria é culpada” pode ser representada simbolicamente por ( ~Q) ⇔ (~R).
Resolução
~Q: Paulo é mentiroso.
~R: Maria é culpada
Veja que a proposição utiliza o conectivo condicional e pode ser representada da seguinte forma:
~Q ⇒ ~R
Resposta: Errado
Questão 54. Se ficar comprovado que apenas um dos quatro envolvidos no ilícito penal é culpado, então a proposição simbolizada por (~P) –> (~Q) v R será verdadeira.
Resolução
Toda proposição do tipo A⇒B é equivalente a ~B⇒~A.
Reescrevendo a afirmação:
Se a proposição simbolizada por (~P)⇒(~Q) ∨ R é falsa, então a quantidade de culpados entre os quatro envolvidos no ilícito penal é diferente de um.
Construindo a tabela verdade, é possível verificar que (~P)⇒(~Q) ∨ R é falsa apenas quando P, Q e R são falsas.
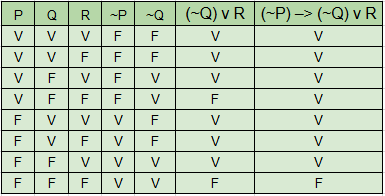
Na questão 51, vimos que se P, Q e R forem falsas, então pelo menos duas pessoas são culpadas, ou seja, a quantidade é diferente de um.
Resposta: Certo.
Questão 55. Independentemente de quem seja culpado, a proposição {P⇒(~Q)}⇒{Q∨[(~Q)∨R]} será sempre verdadeira, isto é, será uma tautologia.
Resolução
Dizemos que uma proposição é uma tautologia quando é verdadeira para todas as situações possíveis.
Verificaremos então se a proposição em questão pode ser falsa.
Como temos uma condicional, a única forma de torná-la falsa é quando V⇒F, ou seja, necessitamos que P⇒(~Q) seja verdadeiro e que Q∨[(~Q)∨R] seja falso.
Para que Q∨[(~Q)∨R] seja falso, é necessário que Q e (~Q)∨R sejam falsos. Mas (~Q)∨R será falso apenas quando (~Q) e R forem falsos.
Veja que teríamos que ter Q e (~Q) falsos simultaneamente, que é impossível.
Conclusão: A proposição em questão não pode ser falsa.
Resposta: Certo
Questão 56. As proposições P∧(~Q)⇒(~R) e R⇒[Q∧(~P)] são equivalentes.
Resolução
Temos que proposições do tipo A⇒B e ~B⇒~A são equivalentes, ou seja, basta inverter e negar as proposições.
A única falha da questão é que a negação de P∧(~Q) é Q∨(~P) e não Q∧(~P).
Resposta: Errado.
Em um aeroporto, 30 passageiros que desembarcaram de determinado voo e que estiveram nos países A, B ou C, nos quais ocorre uma epidemia infecciosa, foram selecionados para ser examinados. Constatou-se que exatamente 25 dos passageiros selecionados estiveram em A ou em B, nenhum desses 25 passageiros esteve em C e 6 desses 25 passageiros estiveram em A e em B.
Com referência a essa situação hipotética, julgue os itens que se seguem.
Questão 57. A quantidade de maneiras distintas de se escolher 2 dos 30 passageiros selecionados de modo que pelo menos um deles tenha estado em C é superior a 100.
Resolução
Em um universo de 30 passageiros, 25 não estiveram em C, ou seja, 5 estiveram em C.
Como queremos que pelo menos um tenha estado em C, calcularemos para exatamente 1 e para 2.
Calculando a quantidade de maneiras de se escolher 2 passageiros, sendo que apenas um deles tenha estado em C, temos que 5 estiveram e 25 não.
5.25 = 125
Calculando a quantidade de maneiras de se escolher 2 passageiros, sendo que ambos estiveram em C, temos uma combinação dos 5 que estiveram, tomados 2 a 2.
C5,2 = 5!/3!.2! = 10
Total: 125 + 10 = 135
Resposta: Certo
Questão 58. Considere que, separando-se o grupo de passageiros selecionados que visitou o país A, o grupo que visitou o país B e o grupo que visitou o país C, seja verificado, em cada um desses grupos, que pelo menos a metade dos seus componentes era do sexo masculino. Nessa situação, conclui-se que o grupo de 30 passageiros selecionados tem, no máximo, 14 mulheres.
Resolução
Como 5 visitaram o país C, podemos concluir que existem, no máximo, 2 mulheres neste grupo.
Dos 25 que sobraram, um grupo possui uma quantidade par e outro grupo possui uma quantidade ímpar de passageiros.
Na melhor das hipóteses, no grupo que possui a quantidade par, podemos considerar que a quantidade de homens e mulheres é igual.
Da mesma forma, no grupo que possui a quantidade ímpar, existe um homem a mais.
Conclusão, devem existir, no mínimo, 2 homens a mais.
Como são 30 pessoas, existem, no máximo, 14 mulheres.
Resposta: Certo
Questão 59. Se 11 passageiros estiveram em B, então mais de 15 estiveram em A.
Resolução
n(A ou B) = n(A) + n(B) – n(A e B).
25 = n(A) + 11 – 6.
n(A) = 20.
Resposta: Certo
Questão 60. Se 2 dos 30 passageiros, selecionados forem escolhidos ao acaso, então a probabilidade de esses 2 passageiros terem estado em 2 desses países é inferior a 1/30.
Resolução
Calculando o total de possibilidades:
C30,2 = 30!/28!.2! = 30.29/2 = 435
Como 6 passageiros estiveram em 2 países, calcularemos a quantidade de maneiras possíveis de se escolher 2 passageiros em 6:
C6,2 = 6!/4!.2! = 6.5/2 = 15
Calculando a probabilidade:
15 / 435 = 15/435 = 1/29 > 1/30.
Gabarito: Certo
Gostou da prova resolvida da PF 2018?
Deixe o seu comentário.
