Confira aqui a prova resolvida do concurso para a GCM SP 2022 (Guarda Civil Metropolitana do Estado de São Paulo), prova aplicada em 2022 pela banca IBADE.
Questão 11. Considere a seguinte equação:
95 . 32 / 814
O resultado dessa equação é:
(A) 34
(B) 32
(C) 3-2
(D) 1/34
(E) -34
Resolução
Observe que não se trata de uma equação, mas de uma expressão numérica, que pode ser resolvida através das potências de 3.
95 . 32 / 814
(3²)5 . 32 / (34)4
32×5 . 32 / 34×4
310 . 32 / 316
310+2 / 316
312 / 316
312-16
3-4
1/34
Resposta: D
Questão 12. Considere a seguinte sequência:
0 – (1/3) – (-9) – (1/27) – …
O sétimo item da sequência é:
(A) -1/729
(B) 729
(C) -729
(D) 1/729
(E) 1/243
Resolução
Observe que:
- os números 3, 9, 27, …, são potências de 3;
- o sinal do expoente está se alternando entre negativo e positivo;
- o sinal de cada elemento da sequência também está alternando entre positivo e negativo.
Com essas informações, podemos listar os próximos termos da sequência:
0; (1/3); (-9); (1/27); (-81); (1/243); (-729)
Reposta: C
Questão 13. Hugo fez um investimento em uma corretora e queria conhecer o valor total que ele possuía nesse investimento após 3 (três) meses. Sabendo que o investimento inicial foi de R$ 5.000,00, que ao final do primeiro mês houve uma valorização de 3%, que ao final do segundo, houve uma desvalorização de 5% e que no último, houve uma valorização de 8%, o valor total que o Hugo possuía ao final dos 3 meses era:
(A) R$ 5.300,00.
(B) R$ 5.250,50.
(C) R$ 5.344,70.
(D) R$ 5.283,90.
(E) R$ 5.435,80.
Resolução
Valor inicial: R$ 5.000,00.
Valor ao final do primeiro mês, com valorização de 3%:
5000 x 3% = 150
Total: 5000 + 150
Valor ao final do segundo mês, com desvalorização de 5%:
5150 x 5% = 257,50
Total: 5150 – 257,50 = 4892,50
Valor ao final do terceiro mês, com valorização de 8%:
4892,50 x 8% = 391,40
Total: 4892,50 + 391,40 = R$ 5.283,90
Resposta: D
Questão 14. Notação científica é uma maneira de escrever números muito grandes ou pequenos. Um número está escrito em notação científica quando temos um número entre 1 e 10 multiplicado por uma potência de 10. Por exemplo: o número 67.200.000 pode ser escrito na notação científica como 6,72.107 e o número 0,0023 pode ser escrito como 2,3.10-3. Considere a seguinte equação:
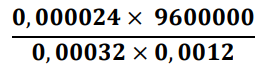
O resultado da equação acima em notação científica é:
(A) 6.10-8
(B) 3.108
(C) 6.1010
(D) 6.10-10
(E) 6.108
Resolução
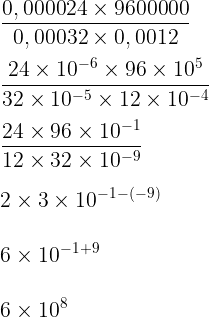
Resposta: E
Questão 15. Em um escritório de advocacia há 30 funcionários no total. Sabendo que a quantidade de mulheres excede a de homens em 8, o número de mulheres, em relação ao número total de funcionários, corresponde a:
(A) 19/30.
(B) 21/30.
(C) 2/3.
(D) 22/30.
(E) 3/5.
Resolução
Considere que “m” representa a quantidade de mulheres e “h” a quantidade de homens.
m + h = 30
m – h = 8
Temos aqui um sistema de equações do primeiro grau. Faremos a soma das duas equações, anulando a incógnita “h”.
m + h + m – h = 30 + 8
2m = 38
m = 38/2
m = 19
Considerando que existem 19 mulheres em um universo de 30 funcionários, a relação buscada é 19/30.
Resposta: A
Questão 16. 12 funcionários de uma empresa de construção realizaram dois quintos de um serviço. Essa parte do serviço demandou um total de 5 dias, nos quais os funcionários trabalharam 8 horas diárias. Para o restante do serviço, que deverá ser concluído em 10 dias, 10 funcionários irão trabalhar. Sabendo que os 10 funcionários irão trabalhar um mesmo número de horas por dia, o total de horas trabalhadas por cada funcionário é de:
(A) 7 dias e 8 minutos.
(B) 7 dias.
(C) 8 dias e 15 minutos.
(D) 7 dias e 40 minutos.
(E) 7 dias e 12 minutos.
Resolução
A questão pode ser resolvida através da regra de três composta.
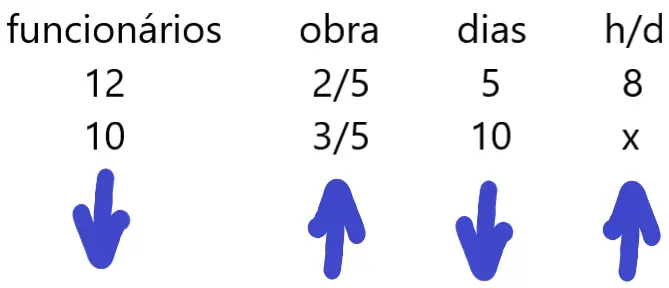
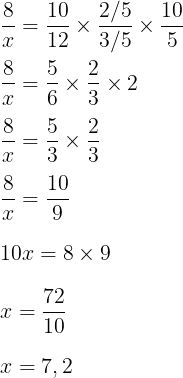
Observe que cada funcionário deverá trabalhar 7,2 horas por dia.
Vamos calcular a quantidade de minutos que equivalem a 0,2 horas?
0,2 = 2/10 = 1/5
Observe que 1/5 de 60 minutos é igual a 60/5 = 12 minutos
Resposta: 7 horas e 12 minutos por dia.
Não temos nenhuma alternativa correta.
Observe que a resposta correta seria a letra E, caso a banca não tivesse escrito dias no lugar de horas.
Questão 17. Leonardo acordou atrasado e, ao verificar o relógio, percebeu que o tempo decorrido do dia era igual a dois quintos do tempo até o final do dia. O horário, aproximado, em que Leonardo acordou foi:
(A) 17h e 9min.
(B) 6h e 51min.
(C) 15h e 33min.
(D) 6h e 22min.
(E) 9h e 10min.
Resolução
Considere que, quando Leonardo acordou, faltavam x horas para o final do dia.
Como “o tempo decorrido do dia era igual a dois quintos do tempo até o final do dia”, podemos concluir que havia se passado 2x/5.
Considerando que um dia possui 24 horas, temos que:
x + 2x/5 = 24
5(x + 2x/5) = 5.24
5x + 2x = 120
7x = 120
x = 120/7
Como 119/7 = 17, vamos considerar que:
x = 17 + 1/7
Como um dia possui 24 horas, Leonardo acordou:
24 – (17 + 1/7) = 6 + 6/7 horas
Vamos calcular quantos minutos equivalem a 6/7 horas?
60 minutos . 6/7 = 360/7 = 51,4
Conclusão: Leonardo acordou as 6 horas e 51 minutos.
Resposta: B
Questão 18. Rômulo, ao entrar em uma loja de computadores, avistou um anúncio informando que toda a loja tinha 10% de desconto nas compras à vista. Rômulo foi procurar um item para seu computador e, ao achá-lo, ficou surpreso ao saber que havia um desconto adicional de 8% no item. Considerando que o preço original do item era R$100,00 e que Rômulo pagou à vista, o preço final que ele pagou foi:
(A) R$ 82,00.
(B) R$ 82,40.
(C) R$ 82,80.
(D) R$ 83,20.
(E) R$ 83,40.
Resolução
O produto custava inicialmente R$ 100,00, porém teve um desconto de 8%, ou seja, passou a custar R$ 92,00.
Romulo teve acesso a mais um desconto na hora de pagar, pois a loja estava com um desconto de 10% em todos os produtos para compras à vista.
92 – 10% = 92 – 9,2 = R$ 82,80.
Resposta: C
Questão 19. A união de conjuntos é dada quando há a junção dos elementos dos mesmos. Considere um conjunto X com 55 elementos e um conjunto Y com 30 elementos. O menor número de elementos da união do conjunto X com o conjunto Y é:
(A) 85.
(B) 55.
(C) 30.
(D) 20.
(E) 15.
Resolução
Observe que os conjuntos X e Y possuem 55 e 30 elementos, respectivamente.
A questão deseja saber o menor número possível de elementos da união X com Y. Isto acontece quando o conjunto Y, que possui menos elementos, estão contido no conjunto X. Neste caso, a união terá os 55 elementos de X.
Resposta: B
Questão 20. Considere que em uma sala de aula há N alunos. O professor afirma aos alunos que há, pelo menos, 4 alunos diferentes fazendo aniversário no mesmo mês. Para tornar essa afirmação obrigatoriamente verdadeira, o valor mínimo de N é:
(A) 4.
(B) 12.
(C) 48.
(D) 25.
(E) 37.
Resolução
Observe que 1 ano possui 12 meses, ou seja, se considerarmos a “pior situação possível”, teremos 36 alunos, com três aniversariantes por mês.
Neste caso, bastaria que houvesse mais um aluno para afirmarmos que um mês terá 4 aniversariantes, ou seja, N = 37.
Leia mais em Princípio da Casa dos Pombos.
Resposta: E
Veja o vídeo com a resolução da prova elaborada pela IBADE para o concurso da GCM SP 2022.
Gostou da resolução da prova do concurso para a GCM SP 2022?
Deixe o seu comentário.
