Estudando matemática para concursos? Confira aqui a última prova resolvida do concurso para Escrevente Técnico Judiciário do TJ de SP, realizado em 2012 pela Vunesp.
35. Usando, inicialmente, somente gasolina e, depois, somente álcool, um carro com motor flex rodou um total de 2 600 km na pista de testes de uma montadora, consumindo, nesse percurso, 248 litros de combustível. Sabe-se que nesse teste ele percorreu, em média, 11,5 quilômetros com um litro de gasolina e 8,5 quilômetros com um litro de álcool. Desse modo, é correto afirmar que a diferença entre a quantidade utilizada de cada combustível nesse teste foi, em litros, igual a
(A) 84.
(B) 60.
(C) 90.
(D) 80.
(E) 68.
Seja A a quantidade de litros de álcool e G a quantidade de gasolina. Temos então que:
A + G = 248
G = 248 – A (1)
Sabendo a quantidade de litros utilizada e a média de consumo, temos:
8,5.A + 11,5.G = 2600 (2)
Substituindo a equação (1) na (2):
8,5.A + 11,5.( 248 – A) = 2600
8,5.A + 2852 – 11,5.A = 2600
– 3.A = 2600 – 2852
– 3.A = – 252
3.A = 252
A = 252/3
A = 84
Calculando G:
G = 248 – A = 248 – 84 = 164
A diferença será: 164 – 84 = 80 litros
36. Do valor total recebido pela venda de um terreno, Ricardo separou 20% para custear uma pequena reforma em sua casa e reservou o restante para a compra de um carro novo. Sabe-se que 60% do valor separado para a reforma foi usado na compra de material de construção, e o restante, no pagamento da mão de obra. Sabendo-se que Ricardo gastou R$ 6.000,00 com a mão de obra empregada na reforma,pode-se afirmar que, para a compra do carro novo, Ricardo reservou
(A) R$ 50.000,00.
(B) R$ 65.000,00.
(C) R$ 60.000,00.
(D) R$ 75.000,00.
(E) R$ 70.000,00.
Temos que:
Valor da mão de obra = 40% do valor separado para reforma reforma pois 60% foi para material de construção. Assim:
6000 = 40% da reforma
6000 = 0,4.reforma
reforma = 6000/0,4 = 15000
Como 20% do valor total foi utilizado para reforma, e esta custou 15000, temos:
15000 = 20% do total
15000 = 0,2.total
total = 15000/0,2 = 75000
Nota-se que Ricardo vendeu o terreno por 75000. Para descobrirmos quanto ele pagou no carro, basta calcularmos quanto é 80% de 75000:
75000.0,8 = 60000
37. Observe a sequência de quadrados, em que a medida do lado de cada quadrado, a partir do segundo, é igual à metade da medida do lado do quadrado imediatamente anterior.
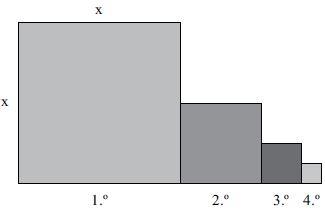 Nessas condições, é correto afirmar que a razão entre a área do 3.º quadrado e a área do 2.º quadrado, nessa ordem, é
Nessas condições, é correto afirmar que a razão entre a área do 3.º quadrado e a área do 2.º quadrado, nessa ordem, é
a) 1/4
b) 1/12
c) 1/10
d) 1/8
e) 1/2
Se chamarmos de w a medida do lado do segundo, temos que o lado do terceiro será w/2. Vamos calcular as áreas:
Área do segundo: w.w = w²
Área do terceiro: (w/2).(w/2) = w²/4
Veja que a área do terceiro é 1/4 menor.
38. Certo capital foi aplicado a juros simples, à taxa de 1,5% ao mês. Para que seja possível resgatar um montante igual a 7/4 do capital inicial, o tempo mínimo que esse capital deverá permanecer aplicado é:
(A) 3 anos e 4 meses.
(B) 3 anos e 9 meses.
(C) 4 anos e 2 meses.
(D) 2 anos e 8 meses.
(E) 2 anos e 10 meses.
Temos que 7/4 = 1,75
Utilizando a fórmula de juros simples:
M = C.(1 + in), onde:
M = Montante (1,75.C)
C = Capital inicial (C)
i = taxa (0,015)
n = prazo em meses
1,75C = C.(1 + 0,015.n)
1,75 = (1 + 0,015.n)
1,75 – 1 = 0,015.n
0,75 = 0,015.n
n = 0,75/0,015
n = 50 meses
Note que 48 meses equivale a 4 anos.
Resposta 4 anos e 2 meses.
