Olá amigos concurseiros! Segue a prova resolvida do concurso para o CRM ES 2016, cargo de Agente Administrativo e aplicada pelo Instituto Quadrix.

A banca foi bem legal para com os candidatos, elaborando questões de fácil resolução para quem se dedicou ao concurso.

Boa sorte a todos!

 

 

Questão 11. Numa pesquisa, verificou-se que, das pessoas consultadas, 100 se informavam pelo site A; 150 por meio do site B; 20 buscavam se informar por meio dos dois sites, A e B; e 110 não se informavam por nenhum desses dois sites. Desse modo, é correto afirmar que o número de pessoas consultadas nessa pesquisa foi de:

a) 380

b) 360

c) 340

d) 270

e) 230

 

Resolução

A questão pode ser facilmente resolvida através do Diagrama de Venn.

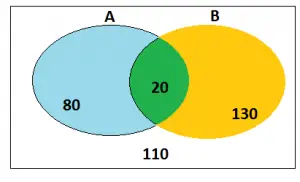
Veja na figura que:

• A região azul corresponde a quantidade de pessoas que se informavam apenas pelo site A (100 – 20).
• A região amarela corresponde a quantidade de pessoas que se informavam apenas pelo site B (150 – 20).
• A região verde corresponde a quantidade de pessoas que se informavam pelos dois sites.
• A região branca corresponde a quantidade de pessoas que não se informavam por nenhum dois dois sites.

O total de pessoas consultadas será:

80 + 20 + 130 + 110 = 340 pessoas

Resposta: C

 

 

Questão 12. Em um campeonato de futebol, uma vitória corresponde a 3 pontos ganhos, um empate corresponde a 1 ponto ganho e, em caso de derrota, não há pontuação. Após cinco jogos disputados nesse campeonato, de quantas maneiras diferentes um time pode obter exatamente cinco pontos?

a) 3

b) 25

c) 30

d) 5

e) 31

 

Resolução

Existem duas opções para, nessas condições, um time conseguir 5 pontos em 5 jogos:

• Empatar todos os jogos.
• Ganhar um, empatar dois e perder dois jogos.

 

Vamos calcular de quantas maneiras a segunda opção pode ocorrer. O que pode ser facilmente calculado através de Anagramas. Veja:

Calculando de quantas sequências diferentes podem ser formadas com as letras V, E, E, D, D, onde V representa vitória, E empate e D derrota.

5! / 2!2! = 120/4 = 30

 

Como o time tem 30 formas diferentes de conseguir uma vitória, dois empates e duas derrotas, além da outra opção que seria empatar todos os jogos, a quantidade total será 31.

Resposta: E

 

 

Questão 13. Num conjunto de 50 parafusos, 40 deles estão em boas condições. Dois desses parafusos são retirados, sucessivamente e ao acaso, sem reposição. Qual é a probabilidade de que o primeiro parafuso defeituoso seja encontrado na 2ª retirada?

a) 8/49

b) 1/5

c) 4/5

d) 8/50

e) 1/4

 

Resolução

A questão informa que o primeiro parafuso a ser retirado deve ser bom, e o segundo deve ser defeituoso.

A probabilidade do primeiro ser bom é de 40/50, pois temos 50 parafusos e 40 são bons.

A probabilidade de tirar um parafuso defeituoso na segunda tentativa é 10/49 (temos 10 defeituosos e agora um total de 49 parafusos).

Basta agora multiplicarmos as probabilidades:

(40/50) x (10/49) = 4/5 x 10/49 = 8/49

 

Resposta: A

 

 

 

 

Questão 14. Uma empresa de telefonia móvel oferece a seus clientes dois tipos de pacotes de serviços:

• Blue 100 – Oferece 100 minutos mensais de ligação local e o usuário deve pagar mensalmente R$ 80,00. Será cobrado o valor de R$ 0,90 por minuto que excede o valor oferecido.
• Blue 300 – Oferece 300 minutos mensais de ligação local e o usuário deve pagar mensalmente R$ 143,00. Será cobrado o valor de R$ 0,40 por minuto que excede o valor oferecido.

Para ser mais vantajoso contratar o pacote Blue 300, comparativamente ao Blue 100, o número mínimo de minutos de ligação que o usuário deverá fazer é:

a) 10

b) 126

c) 171

d) 300

e) 400

 

Resolução

Sendo f(x) = 80 + 0,9(x – 100) a função que representa o valor gasto através do plano Blue 100, vamos calcular quando que o plano Blue 100 se iguala ao plano Blue 300:

80 + 0,9(x – 100) = 143

80 + 0,9x – 90 = 143

0,9x – 10 = 143

0,9x = 143 + 10

0,9x = 153

x = 153 / 0,9

x = 170 minutos

 

Logo, o plano Blue 300 será mais vantajoso a partir de 171 minutos.

Resposta: C

 

 

Questão 15. De todos os estádios utilizados na Copa do mundo do Brasil em 2014, um dos mais belos é o Mané Garrincha, situado em Brasília, com capacidade para 70.000 pessoas. Em certa partida, o estádio estava com 90% de sua capacidade, sendo que 737 pessoas não pagaram o ingresso que custava 150 dólares cada. A expressão que representa o valor arrecadado nesse jogo, em dólares, é:

a) 0,90.70000.150-737

b) 0,90(70000.737).150

c) (0,90.70000-737).150

d) 90.(70000-737).150

e) (90.70000-737).150

 

Resolução

Para calcularmos a arrecadação do jogo, o primeiro passo é calcular 90% de 70 mil, que pode ser calculado pelo produto 0,9.70000. Em seguida devemos descontar os não pagantes. E enfim devemos multiplicar pelo valor do ingresso. Veja:

(0,9.70000 – 737).150

 

Resposta: C