Confira aqui a prova resolvida de matemática do concurso Correios 2008, realizado pela CONSULPLAN, para o cargo de Agente de Correios – Carteiro.
21) Fazer a barba no passado era um ritual que consumia algo como meia hora no barbeiro, tempo necessário para ela ficar de molho em água quente, receber fartas pinceladas de espuma e ser retirada com navalhas finíssimas. Hoje, as pessoas levam cinco minutos para barbear-se em casa. Resolva a expressão numérica abaixo, cujo valor corresponde ao ano em que surgiu a primeira lâmina de barbear descartável:
11² – √100 + 54 . (9:3)0 + (15 – 40 : 8)³ + 11.15
A) 1.821
B) 1.901
C) 1.705
D) 1.796
E) 1.836
Resolução
11² – √100 + 54 . (9:3)0 + (15 – 40 : 8)³ + 11.15
121 – 10 + 625 . 30 + (15 – 5)³ + 165
121 – 10 + 625 . 1 + 10³ + 165
111 + 625 + 1000 + 165
1901
Resposta: B
22) Estima-se que existam por volta de 18.000 espécies de formigas no mundo. No Brasil, são aproximadamente 2.000 espécies, mas apenas de 20 a 30 são consideradas pragas. As demais são muito úteis, pois comem os parasitas das plantas. A quantidade de espécies de formigas no mundo equivale a quantas vezes o número de espécies que existem no Brasil?
A) 36 vezes.
B) 90 vezes.
C) 50 vezes.
D) 9 vezes.
E) 6 vezes.
Resolução
Existem 18000 mil espécies no mundo e 2000 espécies no Brasil.
18000 / 2000 = 18/2 = 9
Resposta: D
23) Na fauna da Mata Atlântica, encontramos cerca de 250 espécies de mamíferos, 1.050 de aves, 197 de répteis, 340 anfíbios e 350 peixes. Apesar dessa riqueza de espécies, a situação é bastante grave, pois das 202 espécies de animais ameaçadas de extinção no Brasil, 171 se encontram na Mata Atlântica. Quantos números citados anteriormente são múltiplos de 3?
A) 5
B) 3
C) 1
D) 2
E) 4
Resolução
A condição para um número ser múltiplo de 3 é que a soma dos seus algarismos seja um múltiplo de três:
250: 2 + 5 + 0 = 7 (NÃO)
1050: 1 + 0 + 5 + 0 = 6 (SIM)
197: 1 + 9 + 7 = 17 (NÃO)
340: 3 + 4 + 0 = 7 (NÃO)
350: 3 + 5 + 0 = 8 (NÃO)
202: 2 + 0 + 2 = 4 (NÃO)
171: 1 + 7 + 1 = 9 (SIM)
Resposta: D
24) Descubra o CEP que está faltando no Cartão Postal de Carol,

sabendo que ele é o resultado da equação abaixo, multiplicado por 104:
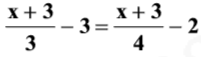
A) 39.000
B) 15.000
C) 90.000
D) 30.000
E) 60.000
Resolução
Observe que existem duas frações na equação, cujos denominadores são 3 e 4.
Multiplicaremos todos os termos da equação por 12, que é o produto entre 3 e 4, para eliminarmos a fração:
12 . [ (x + 3)/3 – 3 = (x + 3)/4 – 2 ]
12.(x + 3)/3 – 12.3 = 12(x + 3)/4 – 12.2
4.(x + 3) – 36 = 3(x + 3) – 24
4x + 12 – 36 = 3x + 9 – 24
4x – 24 = 3x – 15
4x – 3x = – 15 + 24
x = 9
Multiplicando o resultado por 104:
9 . 104 = 9 . 10000 = 90000
Resposta: C
25) A Bíblia nos diz que a arca de Noé tinha 300 côvados de comprimento. Sabendo que um côvado tem 525mm, quantos metros tinha o comprimento da arca de Noé?
A) 175m
B) 157,5m
C) 1.575m
D) 15,75m
E) 1,75m
Resolução
Considerando que 1 metro equivale a 1.000mm (milímetros), um côvado equivale a 0,525 metros.
Calculando o comprimento da arca de Noé:
300 x 0,525 = 157,5 m
Resposta: B
26) Em 2002 no Brasil, constatou-se que pelo menos uma criança ou adolescente trabalhava. Entre eles, 280.228 tinham de 5 a 9 anos, 2.708.066 tinham de 10 a 15 anos e 2.450.261 tinham 16 ou 17 anos. Foi apurado que 51% deles trabalhavam na via pública. Quantas crianças, aproximadamente, trabalhavam em via pública quando foi feita essa pesquisa?
A) 277.315
B) 2.773.663
C) 138.111
D) 277.366
E) 226.336
Resolução
Calculando a quantidade total:
280.228 + 2.708.066 + 2.450.261 = 5.438.555
Calculando quantas trabalhavam em via pública:
5.438.555 x 51% = 2.773.663
Resposta: B
27) Ricardo usa a Internet em horários e dias em que é cobrada uma taxa única a cada vez que faz uma conexão. Assim, gasta mensalmente R$25,00 com o provedor e mais R$3,00 por acesso (conexão). No último mês, conectou a Internet várias vezes e pagou R$85,00. Se esse mês ele conectar o dobro de vezes do mês passado, quanto ele pagará?
A) R$180,00
B) R$170,00
C) R$145,00
D) R$120,00
E) R$154,00
Resolução
Observe que Ricardo pagou R$ 85,00 no último mês.
Descontando o valor fixo, temos:
85 – 25 = R$ 60,00
Considerando que ele paga R$ 3,00 por conexão, podemos calcular a quantidade de conexões:
60 / 3 = 20 conexões
Se este mês ele conectar o dobro, serão feitas 40 conexões:
25 + 40 x 3
25 + 120
R$ 145,00
Resposta: C
28) Amplitude térmica é a diferença entre a temperatura máxima e mínima registrada em um lugar. Num dia de inverno em Berlim(Alemanha), a temperatura mínima registrada foi de –3ºC e a temperatura máxima foi de 2ºC.
Qual foi a amplitude térmica registrada nessa cidade?
A) 5ºC
B) 1ºC
C) 6ºC
D) –5ºC
E) –1ºC
Resolução
Calculando a diferença entre a temperatura máxima e mínima:
2 – (-3) = 2 + 3 = 5
Resposta: A
29) Dados médicos indicam que a ingestão de uma lata de cerveja provoca a concentração de aproximadamente 0,3 gramas por litro de álcool no sangue. Waldir tomou 9 latas de cerveja numa festa com seus amigos, qual a concentração de álcool no sangue provocada pela ingestão dessa quantidade de cerveja?
A) 24g/litro
B) 30g/litro
C) 2,4g/litro
D) 2,7g/litro
E) 1,8g/litro
Resolução
Cada lata provoca a concentração de aproximadamente 0,3 gramas por litro de sangue. Considerando que Waldir tomou 9 latas:
9 x 0,3 = 2,7 g/litro
Resposta: D
30) Jair resolveu aplicar uma parte de seu salário a juros simples de 2,1% ao mês. Qual foi o valor aplicado, sabendo que ele recebeu no final de 1 ano e 3 meses, juros de R$472,50?
A) R$1.464,75
B) R$1.730,70
C) R$150,00
D) R$1.730,00
E) R$1.500,00
Resolução
Observe que a aplicação gerou R$ 472,50 em 15 meses. Com essas informações, podemos calcular o valor gerado mensalmente, considerando que trata-se do regime de juros simples.
472,50 / 15 = R$ 31,50
Considerando que x representa o valor aplicado, e que 0,021 é a representação decimal de 2,1%, temos:
x . 0,021 = 31,5
x = 31,5 / 0,021
x = 1500
Resposta: E
31) Todos os dias Miguel vai a pé para o serviço. Ele trabalha a 2.208 metros de sua casa e anda ao ritmo de 80 metros por minuto. Quanto tempo ele gastou para ir a pé de sua casa ao trabalho?
A) 17min 10s
B) 27min 6s
C) 27min 36s
D) 17min 36s
E) 14 min 6s
Resolução
Observe que ele trabalha a 2208 metros e anda 80 metros por minuto. Calculando a quantidade de minutos:
2208 / 80 = 27,6 minutos
Para finalizar, precisamos calcular a quantidade de segundos que equivalem a 0,6 segundos.
0,6 x 60 segundos = 36 segundos
Resposta: C
32) Numa viagem a uma cidade do Nordeste, Pedro e Gabriel foram de carro alternando a direção. No primeiro dia, Pedro dirigiu 1/3 da viagem. No segundo dia, Gabriel dirigiu 1/5 da viagem. Os 1.050km restantes da viagem foram percorridos em dois dias. Quantos quilômetros foram percorridos em toda a viagem?
A) 1.610km
B) 2.250km
C) 1.600km
D) 560m
E) 1.540m
Resolução
Sabemos que Pedro dirigiu 1/3 no primeiro dia e que Gabriel dirigiu 1/5 da viagem no segundo dia.
1/3 + 1/5 = (5 + 3)/15 = 8/15
A questão ainda informa que o restante equivale a 1050 km, ou seja, essa distância equivale a 7/15 da viagem.
Considerando que x representa a distância total, temos:
x.7/15 = 1050
x = 1050.15/7
x = 2250 km
Resposta: B
33) Andando a pé 8 horas por dia, um Carteiro conseguiu em 10 dias percorrer a distância de 320km. Quantas horas por dia ele deverá andar para percorrer em 6 dias a distância de 240km?
A) 10h/dia
B) 12h/dia
C) 4h/dia
D) 5h/dia
E) 9h/dia
Resolução
Temos aqui uma questão que envolve regra de três composta:
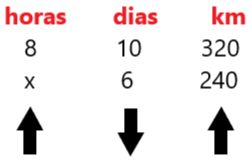
x/8 = 10/6 . 240/320
x/8 = 5/3 . 3/4
x/8 = 5/4
x = 8.5/4
x = 10 horas
Resposta: A
34) Para a confecção de sacolas serão usados dois rolos de fio de nylon. Esses rolos, medindo 450cm e 756cm serão divididos em pedaços iguais e do maior tamanho possível. Sabendo que não deve haver sobras, quantos pedaços serão obtidos?
A) 25
B) 42
C) 67
D) 35
E) 18
Resolução
O nosso objetivo é dividir os dois rolos em partes iguais, sem sobras e com o maior tamanho possível, ou seja, precisamos encontrar o máximo divisor comum de 450 e 756.
Fatorando os números:
450 = 2.3².5²
756 = 2².3³.7
MDC(450, 756) = 2.3² = 18
Resposta: E
35) Dona Tida comprou: 5 pacotes de açúcar de 2kg cada um; 10 pacotes de maizena com 600g cada um; 20 pacotes de margarina de 250g cada um. Qual a massa total dessa compra?
A) 2,1kg
B) 21kg
C) 11.100g
D) 2.100g
E) 855g
Resolução
600g = 0,6 kg
250g = 0,25 kg
Massa total:
5 x 2 + 10 x 0,6 + 20 x 0,25
10 + 6 + 5
21 kg
Resposta: B
36) Em Marte, as estações climáticas, os dias e os anos têm uma duração diferente da Terra. O dia em Marte tem, aproximadamente, 0,5 horas a mais que na Terra e a duração do ano por lá é igual a 1,9 vezes a duração do ano aqui na Terra. Considerando o ano de 365 dias, quantos dias tem o ano marciano?
A) 912,5 dias.
B) 182,5 dias.
C) 192,1 dias.
D) 96,05 dias.
E) 693,5 dias.
Resolução
O gabarito oficial tem como resposta a letra E.
A banca simplesmente multiplicou 365 dias por 1,9, que é igual a 693,5 dias.
Mas neste caso, não estamos considerando a informação do enunciado, que afirma que o dia em Marte tem aproximadamente 24,5 horas.
Resolução correta
Quantidade de horas em um ano terrestre:
365 dias x 24 horas = 8760 horas
A duração do ano em Marte é 1,9 vezes maior:
1,9 x 8760 = 16644 horas
Quantidade de dias com 24,5 horas de duração:
16644 / 24,5 = 679,34 dias
37) A mãe de Eduardo foi ao caixa eletrônico de um Banco, enquanto ele jogava futebol com sua turma. A que horas ela deve buscar Eduardo, se o jogo começou às 16h e 30min e cada um dos dois tempos do futebol de salão infantil dura um quarto de hora e o intervalo entre os dois tempos é de apenas 5min?
A) 17h e 25min.
B) 17 e 15min.
C) 17h e 5min.
D) 17h e 30min.
E) 18h e 5min.
Resolução
Observe que 1/4 de hora é equivalente a 15 minutos, considerando que uma hora possui 60 minutos.
Tempo total de Eduardo no futebol:
15 + 15 + 5 = 35 minutos
Considerando que o jogo começou às 16h e 30min e dura exatamente 35 minutos, a mãe deve buscar Eduardo às 17h e 05min.
Resposta: C
38) Ananias contratou um Engenheiro para gerenciar a construção de um prédio, o qual pediu um prazo de entrega de 8 meses com 14 pedreiros trabalhando. Sabendo-se que Ananias precisa do prédio pronto em 120 dias, quantos pedreiros serão necessários para p término dessa construção no prazo pretendido?
A) 7
B) 21
C) 60
D) 15
E) 28
Resolução
O engenheiro informou que consegue entregar a obra em 8 meses, trabalhando com 14 pedreiros.
Ananias precisa do prédio em 120 dias, ou seja, 4 meses, que é metade do tempo.
Neste caso, o engenheiro deve dobrar a quantidade de pedreiros.
2 x 14 = 28 pedreiros
Resposta: E
39) Em 1994, o real foi instituído como unidade do Sistema Monetário Brasileiro, mantendo-se os centavos. Foi estabelecido que dois mil, setecentos e cinquenta cruzeiros reais era igual a um real. Então, CR$2.750,00 passou a valer R$1,00. Como ficou o saldo bancário de Sr. Silva sabendo que ele possuía no banco a quantia de CR$2.062.500,00?
A) R$556,80
B) R$1.031,25
C) R$567,18
D) R$750,00
E) R$2.062,50
Resolução
A taxa de conversão da época foi de CR$2.750,00 = R$1,00.
Considerando que o Sr. Silva possuía CR$2.062.500,00, temos:
2.062.500 / 2.750
206250 / 275
R$ 750,00
Resposta: D
40) Laura pagou com quatro notas de R$10,00 uma compra de R$39,00 que fez na barraca de frutas. Sabe-se que o feirante possui cédulas de R$5,00 para efetuar troco. De quanto ele necessita para o troco?
A) R$4,00
B) R$1,00
C) R$5,00
D) R$3,00
E) R$2,00
Resolução
Considerando que ela pagou com 4 notas de 10 reais, ela repassou R$ 40,00 para o feirante.
A compra foi de R$ 39,00, ou seja, ele necessita de R$ 1,00 de troco.
Resposta: B
Observação: O gabarito oficial apresenta a letra A como resposta, porém claramente existe um erro e a questão deveria ter sido revidada.
Gostou da prova resolvida do concurso Correios 2008? Deixe o seu comentário.
