Confira aqui a última prova resolvida do concurso para o BRB, cargo de escriturário, prova aplicada em 2011 pelo CESPE.
Lembrando que em nosso site você encontra várias provas resolvidas de carreiras bancárias e da banca CESPE.
Bom estudo!
Considerando que, em uma progressão aritmética de termos a1, a2, … , an, …, a razão seja positiva, a1 = 2 e os termos a1, a3 e a11 estejam, nessa ordem, em progressão geométrica, julgue os itens a seguir.
Resolução
Calcularemos as razões das progressões para descobrimos cada um de seus termos.
Sendo r a razão da P.A., temos:
a1 = 2
a2 = 2 + r
a3 = 2 + 2r
…
a11 = 2 + 10r
Sendo q a razão da P.G. formada pelos termos a1, a3 e a11 da P.A., temos:
a1 = 2
a3 = 2q
a11 = 2q²
Igualando os termos a3 e a11, temos:
2q = 2 + 2r
2q² = 2 + 10r
Temos um sistema de duas equações e duas incógnitas que pode ser simplificado por 2:
q = 1 + r
q² = 1 + 5r
Substituindo a equação 1 na 2, temos:
(1 + r)² = 1 + 5r
1 + 2r + r² = 1 + 5r
r² – 3r = 0
r(r – 3) = 0
r = 0 ou r = 3
Como r>0, consideramos r = 3.
Calculando q:
q = 1 + r
q = 1 + 3
q = 4
Sabendo as razões das progressões, podemos determinar cada um de seus elementos:
P.A.: 2, 5, 8, 11, 14, 17, 20, 23, 26, 29, 32, …
P.G.: 2, 8, 32, …
Questão 91. Para cada n ímpar, an será sempre um número par.
Basta observar na P.A. que os elementos de ordem ímpar são pares.
Resposta: C
Questão 92. A razão dessa progressão aritmética será um número racional, não inteiro.
r = 3 é um número racional e inteiro
Resposta: E
Questão 93. A média aritmética de 3 termos quaisquer dessa progressão aritmética será sempre um número inteiro.
Sabemos que a progressão aritmética possui razão igual a 3.
Considere 3 termos quaisquer, onde x, y e z são números inteiros positivos.
2 + 3x, 2 + 3y, 2 + 3z
Calculando a média aritmética:
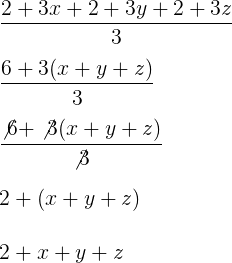
Como x, y e z são números inteiros, a média 2 + x + y + z também será.
Resposta: C
Em uma cidade, 1.000 habitantes foram entrevistados a respeito de suas relações com os bancos A e B. Dos entrevistados, 450 eram correntistas apenas do banco A, 480 eram correntistas do banco B, 720 eram correntistas de apenas um desses bancos e o restante não era correntista de nenhum desses 2 bancos.
Resolução
A questão pode ser resolvida através do Diagrama de Venn.
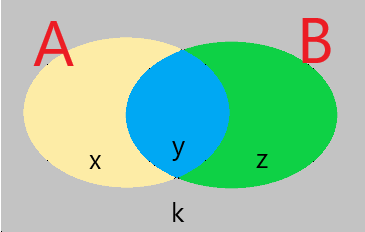
No diagrama, temos:
- x = quantidade de pessoas que são correntistas apenas do Banco A
- y = quantidade de pessoas que são correntistas dos dois bancos
- z = quantidade de pessoas que são correntistas apenas do banco B
- k = quantidade de pessoas que não não correntistas de nenhum dos dois bancos
Analisando as informações do enunciado, temos:
x = 450
y + z = 480
x + z = 720
k = 1000 – x – y – z
Podemos descobrir o valor de z substituindo o valor de x na terceira equação:
x + z = 720
450 + z = 720
z = 720 – 450
z = 270
Podemos descobrir o valor de y substituindo o valor de z na segunda equação:
y + z = 480
y + 270 = 480
y = 480 – 270
y = 210
Calculando a quantidade de pessoas que não são correntistas de nenhum dos dois bancos:
k = 1000 – x – y – z
k = 1000 – 450 – 210 – 270
k = 70
A respeito dessa pesquisa, é correto afirmar que a probabilidade de um dos entrevistados
Questão 94. ser correntista dos 2 bancos é superior a 0,20.
Como y = 210, esse é o número de pessoas que são correntistas dos dois bancos.
Calculando a probabilidade:
210 / 1000 = 0,21
Resposta: C
Questão 95. não ser correntista de nenhum dos bancos é igual a 0,08.
Como k = 70, esse é o número de pessoas que não são correntistas de nenhum dos dois bancos.
Calculando a probabilidade:
70 / 1000 = 0,07
Resposta: E
Questão 96. ser correntista apenas do banco B é inferior a 0,25.
Como z = 270, esse é o número de pessoas que são correntistas apenas do banco B.
Calculando a probabilidade:
270 / 1000 = 0,027
Resposta: E
Você conferiu a prova resolvida do concurso para o Banco Rural de Brasília (BRB), aplicada em 2011 pelo CESPE.
Deixe o seu comentário.
