Confira aqui a prova de matemática resolvida do concurso para Bombeiros do Estado do Piauí, organizado em 2017 pela NUCEPE.
Boa sorte!
QUESTÃO 13. Inflação é nada mais nada menos que a perda do valor do dinheiro. Pareceu fácil demais esta definição? Bom, vamos então expandir sua visão! A inflação é quando o valor do dinheiro é desvalorizado assim diminuindo seu poder de compra, como no exemplo: Todo mês um trabalhador recebe R$100,00 por seu trabalho e com este dinheiro compra um saco de feijão por R$10,00. Nos jornais é anunciado que a inflação deste país é de 10% ao mês. No mês seguinte, este mesmo trabalhador quando for comprar seu saco de feijão vai encontrar seu preço a R$11,00. Mas porque houve este aumento? O que houve foi que a inflação reajustou o valor do alimento em 10% (10% x R$10,00 = R$1,00) enquanto que o salário do trabalhador manteve-se em seu valor antigo. Podemos assim concluir que o poder de compra deste trabalhador diminuiu devido ao aumento do preço dos alimentos.
Disponível em: http://economiasemsegredos.com/o-que-e-inflacao-como-calcular. Acesso em 10/10/2017.
Se no exemplo acima o trabalhador tivesse um aumento salarial de 4,5%, qual seria a perda do seu poder de compra?
A) 5%
B) 5,5%
C) 6%
D) 6,5%
E) 10%
Resolução
Observe que o salário do trabalhador foi valorizado em 4,5%, enquanto a inflação foi de 10%.
Podemos utilizar a fórmula da taxa real:
(1 + in) = (1 + ir).(1 + if)
Onde:
in = taxa nominal = 4,5%
ir = taxa real = ?
if = taxa inflação = 10%
(1 + in) = (1 + ir).(1 + if)
1 + 0,045 = (1 + ir).(1 + 0,10)
1,045 = (1 + ir).(1,1)
(1 + ir) = 1,045 / 1,1
(1 + ir) = 0,95
ir = 0,95 – 1
ir = – 0,05 (inflação de 5%)
Resposta: A
QUESTÃO 14. ANULADA
QUESTÃO 15. O major Cássio é o responsável pelo corpo de bombeiros em Felicidade. Ontem à noite ele recebeu um comunicado para resgatar um gato que ficou preso próximo à sacada de um apartamento no 9º andar de um prédio. Os moradores do edifício informaram que o dono do apartamento está viajando para o exterior e não tem previsão de retorno. A equipe do Cássio fez um levantamento e constatou que a base da escada, localizada sobre o caminhão do corpo de bombeiros, deve ficar a uma distância de 7,15 metros da parede do prédio. Além disso, sua equipe também descobriu, através de uma análise do projeto arquitetônico, que cada um dos andares do prédio (incluindo o térreo) mede 3 metros de altura. Sabendo que o caminhão do corpo de bombeiros tem 2 metros de altura, qual o comprimento mínimo (aproximado) que a escada deve ter para atingir a altura da sacada em que está o gato?
A) 29 metros.
B) 28 metros.
C) 27 metros.
D) 26 metros.
E) 24 metros.
Resolução
As informações apresentadas no enunciado da questão estão na figura abaixo.
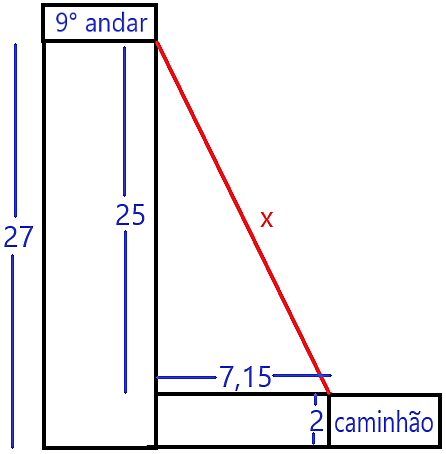
Veja que o piso do 9° andar está localizado a 27 metros do solo (cada andar e térreo possuem 3 metros de altura), o caminhão possui 2 metros de altura e está a 7,15 metros de distância do prédio, e x representa o comprimento da escada, que pode ser calculado através do Teorema de Pitágoras.
x² = 25² + 7,15²
x² = 625 + 51,1
x² = 676,1
x = √676,1
x = 26 metros
Resposta: D
QUESTÃO 16. O casal Maria e José comprou um terreno retangular de 30 metros de comprimento por 20 metros de largura para construir sua casa. O arquiteto contratado para fazer o projeto programou uma casa retangular de 264 metros quadrados de área construída. Maria disse que quer a casa centralizada com as paredes externas equidistantes do muro. Qual o perímetro da casa do casal Maria e José?
A) 70 metros.
B) 68 metros.
C) 66 metros.
D) 64 metros.
E) 62 metros.
Resolução
O terreno retangular possui dimensões 30 m x 20 m.
Maria deseja uma casa centralizada, com paredes externas equidistantes do muro.
Consideraremos que a distância da casa até o muro em todos os lados da casa é igual a x, ou seja, a casa terá as medidas 30 – 2x e 20 – 2x.
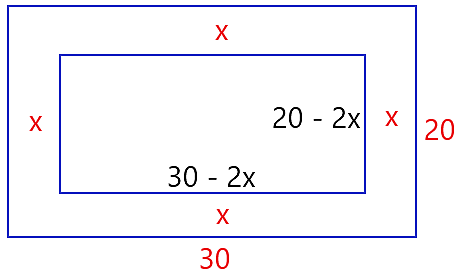
Considerando que a área será igual a 264 m², temos que:
(30 – 2x).(20 – 2x) = 264
600 – 60x – 40x + 4x² – 264 = 0
4x² – 100x + 336 = 0
x² – 25x + 84 = 0
Utilizaremos a fórmula de Bháskara para calcular o valor de x na equação do segundo grau.
∆ = b² – 4ac
∆ = (-25)² – 4.1.84
∆ = 625 – 336
∆ = 289
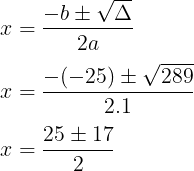
x’ = (25 + 17)/2 = 42/2 = 21
x’’ = (25 – 17)/2 = 8/2 = 4
Observe que x não pode ser igual a 21, logo, consideraremos x = 4.
30 – 2x = 30 – 2.4 = 30 – 8 = 22
20 – 2x = 20 – 2.4 = 20 – 8 = 12
Perímetro:
22 + 22 + 12 + 12 = 68
Resposta: B
QUESTÃO 17. Analise as afirmações a seguir:
I. Um agricultor tem 40 filas de pés de manga, cada uma com 20 árvores. Se uma árvore produz 18 caixas de manga, então esse agricultor irá colher 14400 caixas de manga.
II. Para numerar as 150 primeiras páginas de um livro são necessários 35 algarismos 3.
III. Se um polígono regular convexo tem ângulo externo igual a 24°, então seu número de diagonais é um divisor de 120.
IV. Se a soma dos n primeiros termos de uma sequência é dada por
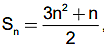
então o terceiro termo dessa sequência é igual a 8. Assinale a alternativa CORRETA.
A) Todas as afirmações são verdadeiras.
B) Apenas I, II e IV são verdadeiras.
C) Apenas I, III e IV são verdadeiras.
D) Apenas I e IV são verdadeiras.
E) Apenas I e III são verdadeiras.
Resolução
Analisaremos cada uma das alternativas.
I. São 40 filas, com 20 árvores cada. Com esta informação é possível calcular a quantidade de árvores:
40 x 20 = 800 árvores
Cada árvore produz 18 caixas, então 800 árvores produzem:
800 x 18 = 14400 caixas
VERDADEIRA
II. De 1 a 150, existem 15 algarismos 3 nas unidades.
Analisando as dezenas, temos 10 algarismos 3 de 30 a 39 e mais 10 de 130 a 139.
Total:
15 + 10 + 10 = 35
VERDADEIRA
III. Considerando que o ângulo externo do polígono regular mede 24°, podemos calcular a quantidade de lados através da seguinte fórmula:
Ae = 360°/n
24° = 360°/n
n = 360°/24°
n = 15 lados
d = n(n – 3)/2
d = 15(15 – 3)/2
d = 15.12/2
d = 90
90 não é divisor de 120
FALSA
IV. Calcularemos inicialmente a soma dos 3 primeiros termos:
S3 = (3n² + n)/2
S3 = (3.3² + 3)/2
S3 = (3.9 + 3)/2
S3 = (27 + 3)/2
S3 = 30/2
S3 = 15
Calculando a soma dos 2 primeiros termos:
S2 = (3n² + n)/2
S2 = (3.2² + 2)/2
S2 = (3.4 + 2)/2
S2 = (12 + 2)/2
S2 = 14/2
S2 = 7
O terceiro termo da sequência é a diferença entre a soma dos três primeiros termos e a soma dos dois primeiros termos.
a3 = S3 – S2 = 15 – 7 = 8
VERDADEIRA
Resposta: B
QUESTÃO 18. Marcos completou o tanque do seu carro com 20 litros de gasolina e pagou R$ 76,00. Marcone também completou o tanque do seu carro com gasolina, nesse mesmo posto, para fazer uma viagem de Teresina a Marcolândia (415 km) e pagou R$ 152,00. O carro de Marcone tinha 5 litros de gasolina no tanque, antes dele abastecer, e faz 11 quilômetros com um litro de gasolina. De acordo com os dados acima, assinale a alternativa CORRETA.
A) Sabendo que o carro de Marcone tem uma reserva de 5 litros, então ele abasteceu seu carro novamente em Picos, cidade situada a 315 km de Teresina, pois acabara de entrar na reserva.
B) Com apenas um tanque de combustível não é possível Marcone fazer a viagem de Teresina a Marcolândia sem reabastecer seu carro.
C) Se Marcone andar a uma velocidade média de 80 km/h e sair de Teresina às 8 horas da manhã, então meio dia estará em Marcolândia.
D) Marcone fará a viagem de Teresina a Marcolândia sem reabastecer o carro.
E) O tanque do carro de Marcos comporta 45 litros.
Resolução
Como Marcos pagou R$ 76 por 20 litros, é possível calcular o preço por litro de gasolina:
76 / 20 = R$ 3,80
Marcone completou o tanque com R$ 152. Como cada litro custa R$ 3,80, é possível calcular a quantidade de litros:
152 / 3,80 = 40 litros
Mas o carro já estava com 5 litros, ou seja, passou a ter 45 litros.
A questão informou que o carro de Marcone faz 11 km por litro de gasolina.
45 x 11 = 494 km
Como a distância de Teresina a Marcolândia é de 415 km, será possível fazer a viagem sem reabastecer o carro.
Resposta: D
QUESTÃO 19. Julgue as afirmações seguintes:
I. Suponha que o caminhão do corpo de bombeiros comporta 1800 litros de água para emergências. Uma piscina, completamente cheia, que tem o formato de um paralelepípedo reto retângulo de 2,3 m de comprimento, 1,5 m de largura e 60 cm de altura tem água suficiente para abastecer o caminhão do corpo de bombeiros.
II. Suponha que o caminhão do corpo de bombeiros custa US$ 600 mil. Se um dólar vale R$ 3,30, então o caminhão de bombeiros custa menos de dois milhões de reais.
III. Suponha que cada mangueira do caminhão do corpo de bombeiros libera 450 litros de água por minuto. Se o caminhão dispõe apenas da reserva de 1800 litros de água, então ligando 5 mangueiras simultaneamente, em menos de quarenta segundos a água do caminhão do corpo de bombeiros acabará.
Marque a alternativa CORRETA.
A) Todas as afirmações são falsas.
B) Apenas II e III são verdadeiras.
C) Apenas I e II são verdadeiras.
D) Apenas I e III são verdadeiras.
E) Todas as afirmações são verdadeiras.
Resolução
Analisaremos cada uma das afirmações.
I. Calcularemos inicialmente o volume da piscina:
2,3 x 1,5 x 0,6 = 2,07 m³
Sabendo que 1 m³ equivale a 1000 litros, podemos concluir que a piscina possui 2070 litros, ou seja, ela é suficiente para encher o caminhão.
VERDADEIRA
II. Calculando o preço do caminhão, em reais:
600.000 x 3,30 = R$ 1.980.000
VERDADEIRA
III. Cada mangueira tem vazão de 450 litros por minuto, ou seja, 5 mangueiras têm vazão total de:
450 x 5 = 2250 litros por minuto
Calcularemos quantos litros de água serão liberados em 40 segundos, que equivalem a 2/3 de um minuto.
2250 . 2/3 = 1500 litros
Como o caminhão possui 1800 litros, a água acabará após 40 segundos.
FALSA
Resposta: C
QUESTÃO 20. Uma guarnição do corpo de bombeiros é formada de 6 sargentos, dentre eles João; 20 soldados, sendo um deles Emanuel. O comando geral pretende formar uma turma com 3 sargentos e 4 soldados para fazer um curso de especialização em resgate causado por terremotos. Sabendo que o sargento João já tem direito adquirido para fazer o curso e que, por problemas particulares, o soldado Emanuel não vai poder participar, de quantas maneiras diferentes o comando geral pode montar essa turma de especialização?
A) 116280.
B) 96900.
C) 77520.
D) 48450.
E) 38760.
Resolução
Seriam escolhidos 3 entre 6 sargentos, porém o João já está escolhido, ou seja, temos uma combinação de 5, tomados 2 a 2:
C5,2 = 5!/(5-2)!2! = 5!/3!2! = 10
Seriam escolhidos 4 entre 20 soldados, porém o Emanuel não poderá participar, ou seja, temos uma combinação de 19, tomados 4 a 4:
C19,4 = 19!/(19-4)!4! = 19!/15!4! = 3.876
Total
10 x 3876 = 38.760
Resposta: E
QUESTÃO 21. Baltazar é o artilheiro do Foguinho e tem se especializado em cobrar faltas. Sabe-se que a probabilidade de ele fazer um gol cobrando falta é de 50%. Qual a probabilidade do Baltazar fazer exatamente 2 gols em 5 cobranças de falta?
A) 25%
B) 31,25%
C) 37,25%
D) 42%
E) 50%
Resolução
Considere que A representa acertar e E representa errar.
Baltazar precisa de uma combinação do tipo AAEEE ou AEEEA, por exemplo.
Utilizando os conceitos de probabilidade, os casos possíveis são:
2 x 2 x 2 x 2 x 2 = 32
Os casos favoráveis podem ser calculados através de uma combinação de 2 em 5:
P5,2 = 5!/2!(5-2)! = 10
Probabilidade:
10/32 = 0,3125 = 31,25%
Resposta: B
QUESTÃO 22. Anulada
Gostou da prova de matemática resolvida do concurso para Bombeiros do Estado do Piauí, organizado em 2017 pela NUCEPE?
Deixe o seu comentário.
