Confira aqui a prova resolvida (gabarito extraoficial) do concurso para o Corpo de Bombeiros do Estado da Bahia (CBM BA), aplicada em 06 de agosto de 2017 pelo IBFC.

A banca cobrou 5 questões de matemática e raciocínio lógico e nenhuma delas é passível de anulação.

Boa sorte!

 

 

Questão 16. A área de um triângulo retângulo cuja hipotenusa mede 2√5 cm e um dos catetos mede 4 cm é igual a:

a) 8 cm²

b) 6 cm²

c) 10 cm²

d) 4√5 cm²

e) 4 cm²

 

Resolução

Podemos desenhar o triângulo retângulo a partir das medidas informadas, onde x será a medida do outro cateto.

 

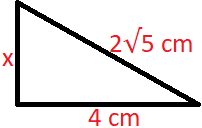
Utilizando o Teorema de Pitágoras:

(2√5)² = x² + 4²

4.5 = x² + 16

20 = x² + 16

x² = 20 – 16

x² = 4

x = √4

x = 2

 

Calculando a área do triângulo:

A = b.h/2

A = 4.2/2

A = 4 cm²

 

Resposta: E

 

 

Questão 17. Carlos cadastrou uma senha de acesso à internet que equivale ao nono termo de uma P.G. (progressão geométrica) cujo primeiro termo é o número 3 e cuja razão é a mesma da P.A.(progressão aritmética): 12,14,….Nessas condições, a senha cadastrada por Carlos foi:

a) 384

b) 768

c) 192

d) 4374

e) 1458

 

Resolução

Percebe-se que a razão da P.A.: 12,14,…. é 2.

Nosso objetivo será calcular o nono termo da P.G. cujo primeiro termo é 3 e a razão é 2.

a_n = a₁.q^n-1

a₉ = 3.2^9-1

a₉ = 3.2⁸

a₉ = 3.256

a₉ = 768

 

Resposta: B

 

 

Questão 18. GeoGebra é um aplicativo gratuito para descrever gráficos através da digitação da equação de uma curva. Ana utilizou esse aplicativo para descrever a equação da reta r: y = 3x – 2. Em seguida digitou a equação da reta s paralela à reta r. Dentre as retas descritas a seguir a equação da reta s digitada por Ana pode ser:

a) s: 3x + 2y – 1 = 0

b) s: 6x – 3y + 2 = 0

c) s: 9x – 3y + 5 = 0

d) s: 2x – 6y + 1 = 0

e) s: 3x + 2y – 4 = 0

 

A maneira mais fácil de verificar se duas retas são paralelas é observando a equação reduzida das retas, onde todas as retas que possuem o mesmo coeficiente angular são paralelas. Veja:

y = mx + n, onde m é o coeficiente angular.

 

Analisando a equação reduzida r: y = 3x – 2, percebemos que o coeficiente angular é 3. Isto ocorre somente na reta s apresentada na opção c. Veja:

9x – 3y + 5 = 0

3y = 9x + 5

y = 3x + 5/3.

Logo, as retas r: y = 3x – 2 e s: 9x – 3y + 5 = 0 são paralelas.

 

Resposta: C

 

 

Questão 19. Para passar num concurso público o candidato deve descrever a equação da figura a seguir:

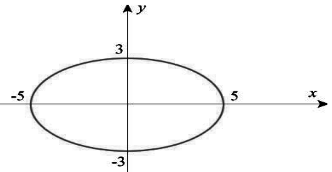
Desse modo, a equação correta da figura é:

 

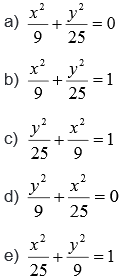
Resolução

Questão bem simples para quem se lembra dos conceitos de cônicas. Temos uma elipse cujo centro é a origem (0,0), o semi eixo menor mede b = 3 e o semi eixo maior mede a = 5. A sua equação é dada por:

x²/5² + y²/3² = 1

x²/25 + y²/9 = 1

 

Resposta: E

 

 

Questão 20. O comandante de uma tropa com 10 soldados irá escolher os 4 melhores soldados para receberem, cada um, uma mesma condecoração. O total de possibilidades distintas de escolha desses 4 soldados é igual a:

a) 5040

b) 2520

c) 420

d) 210

e) 840

 

Resolução

Como a ordem dos soldados é irrelevante, devemos calcular a combinação de 10 soldados, tomados 4 a 4.

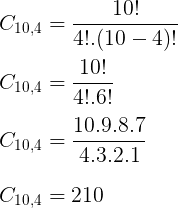
Resposta: D

 

 

Gostou da prova resolvida do concurso para o Corpo de Bombeiros do Estado da Bahia (2017)?

Curta e compartilhe para os seus amigos.