Confira aqui a prova de matemática resolvida do concurso para o cargo de agente comercial do Banco do Brasil, organizado em 2021 pela Cesgranrio.
Boa sorte!
MATEMÁTICA
16. Antes de iniciar uma campanha publicitária, um banco fez uma pesquisa, entrevistando 1000 de seus clientes, sobre a intenção de adesão aos seus dois novos produtos. Dos clientes entrevistados, 430 disseram que não tinham interesse em nenhum dos dois produtos, 270 mostraram-se interessados no primeiro produto, e 400 mostraram-se interessados no segundo produto. Qual a porcentagem do total de clientes entrevistados que se mostrou interessada em ambos os produtos?
(A) 10%
(B) 15%
(C) 20%
(D) 25%
(E) 30%
Resolução
Observe que a pesquisa foi feita com 1000 clientes, e que 430 deles disseram que não tinham interesse em nenhum dos produtos, ou seja, 570 clientes tinham interesse em pelo menos um dos produtos.
Considerando que A representa o conjunto dos clientes que se interessaram no primeiro produto, e que B representa o conjunto dos clientes que se interessaram no segundo produto, é possível desenhar o seguinte diagrama.
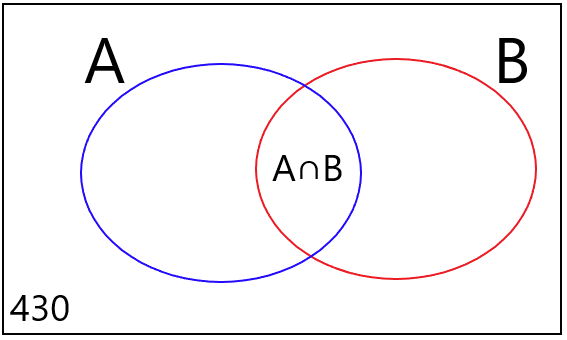
Observe que a questão está interessada nos clientes que demonstraram interesse em ambos os produtos (A∩B). Neste caso, utilizaremos a fórmula que expressa o número de elementos da união de dois conjuntos:
n(AUB) = n(A) + n(B) – n(A∩B)
Onde:
n(AUB) = número de elementos da união dos dois conjuntos
n(A) = número de elementos do conjunto A
n(B) = número de elementos do conjunto B
n(A∩B) = número de elementos da intersecção dos dois conjuntos
n(AUB) = n(A) + n(B) – n(A∩B)
570 = 270 + 400 – n(A∩B)
570 = 670 – n(A∩B)
n(A∩B) = 670 – 570
n(A∩B) = 100
Observe que 100, de um total de 1000 entrevistados, demonstraram interesse em ambos os produtos:
100 / 1000 = 0,10 = 10%
Resposta: A
17. A sequência de Fibonacci é bastante utilizada para exemplificar sequências definidas por recorrência, ou seja, sequências em que se pode determinar um termo a partir do conhecimento de termos anteriores. No caso da sequência de Fibonacci, escreve-se que Tn+2 = Tn+1 + Tn e, desse modo, pode-se obter um termo qualquer conhecendo-se os dois termos anteriores. Considerando o exposto acima, determine o termo T2021 da sequência de Fibonacci, sabendo que T2018 = m e T2020 = p.
(A) (p + m)/2
(B) (p – m)/2
(C) p + 2m
(D) 2p – m
(E) 2m – 2p
Resolução
A partir do terceiro termo, podemos calcular qualquer termo da sequência de Fibonacci através da soma dos dois termos anteriores, ou seja, Tn+2 = Tn+1 + Tn.
O objetivo da questão é calcular o termo T2021 , ou seja, precisamos saber o valor de T2020 e T2019. Observe que sabemos o valor de T2020 e não sabemos o valor de T2019.
O valor de T2019 não é conhecido, mas pode ser calculado através da relação:
T2020 = T2019 + T2018
p = T2019 + m
T2019 = p – m
Agora que sabemos o valor do 2019° termo, podemos utilizar novamente a fórmula para calcularmos o 2021° termo:
T2021 = T2020 + T2019
T2021 = p + p – m
T2021 = 2p – m
Resposta: D
18. J modelou um problema de matemática por uma função exponencial do tipo a(x)=1000ekx, e L, trabalhando no mesmo problema, chegou à modelagem b(x)=102x+3. Considerando-se que ambos modelaram o problema corretamente, e que lnx = logex, qual o valor de k?
(A) ln 2
(B) ln 3
(C) ln 10
(D) ln 30
(E) ln 100
Resolução
Considerando-se que ambos modelaram o problema corretamente, podemos concluir que:
a(x) = b(x)
1000ekx = 102x+3
1000ekx = 10³.102x
1000ekx = 1000.102x
ekx = 102x
ekx = 100x
ln(ekx) = ln(100x)
kx = x.ln100
k = ln100
Resposta: E
19. O método da bisseção é um algoritmo usado para encontrar aproximações das raízes de uma equação. Começa-se com um intervalo [a,b], que contém uma raiz, e, em cada passo do algoritmo, reduz-se o intervalo pela metade, usando-se um teorema para determinar se a raiz está à esquerda ou à direita do ponto médio do intervalo anterior. Ou seja, após o passo 1, obtém-se um intervalo de comprimento (b-a)/2; após o passo 2, obtém-se um intervalo de comprimento (b-a)/4; e após o passo n, obtém-se um intervalo de comprimento (b-a)/2n. Esse processo continua até que o intervalo obtido tenha comprimento menor que o erro máximo desejado para a aproximação. Para aplicar esse método no intervalo [1,5], quantos passos serão necessários para obter-se um intervalo de comprimento menor que 10-3?
(A) 9
(B) 10
(C) 11
(D) 12
(E) 13
Resolução
Observe que à medida que n vai crescendo, o comprimento do intervalo vai ficando cada vez menor, podendo ser calculado através da seguinte fórmula:
C = (b-a)/2n
A questão informa que o método será aplicado no intervalo [1,5], tendo como objetivo obter um intervalo de comprimento menor que 10-3.
C = (5-1)/2n
C = 4/2n
C = 2²/2n
C = 1/2n-2
Observe que devemos ter 10-3 > 1/2n-2.
Como 10-3 = 1/1000, e a primeira potência de 2 que faz a igualdade ser verdadeira é 1/1024 = 1/210, temos que:
1/2n-2 = 1/210
n – 2 = 10
n = 10 + 2
n = 12
Resposta: D
20. Uma loja vende um produto em dois tipos de embalagem: unitária (com uma unidade do produto) e dupla (com duas unidades do produto). Em certo mês, foram vendidas 16 embalagens duplas e 20 unitárias, gerando uma receita para a loja de R$ 488,00. No mês seguinte, foram vendidas 30 embalagens duplas e 25 unitárias, gerando uma receita de R$ 790,00. Qual foi a porcentagem do desconto dado em cada unidade do produto ao se comprar a embalagem dupla?
(A) 5%
(B) 8%
(C) 10%
(D) 12%
(E) 15%
Resolução
Considere que U represente o preço da embalagem unitária e D o preço da embalagem dupla.
No primeiro mês:
16D + 20U = 488
Dividindo-se tudo por 4, temos:
4D + 5U = 122
No segundo mês:
30D + 25U = 790
Dividindo-se tudo por 5, temos:
6D + 5U = 158
Basta agora resolvermos o sistema abaixo, em que faremos a subtração da segunda pela primeira equação:
4D + 5U = 122
6D + 5U = 158
6D + 5U – (4D + 5U) = 158 – 122
6D + 5U – 4D – 5U = 36
2D = 36
D = 36/2
D = 18
Calcularemos o valor de U através da primeira equação:
4D + 5U = 122
4.18 + 5U = 122
72 + 5U = 122
5U = 122 – 72
5U = 50
U = 50/5
U = 10
Observe que a embalagem dupla custa 18 reais, ou seja, cada produto custa 9 reais, enquanto na embalagem unitária, cada produto custa 10 reais. O desconto foi de 1 em 10 reais:
1 / 10 = 0,10 = 10%
Resposta: C
MATEMÁTICA FINANCEIRA
26. Um negociador de investimentos de uma instituição financeira pergunta ao gerente de tal instituição qual a taxa de juros anual máxima que pode oferecer a um cliente investidor, e o gerente afirma que ficará satisfeito com uma taxa anual máxima de 8,36%. O negociador entra em contato com o cliente que pretende investir um capital C1 e diz que, ao final de um ano, ele receberá C2, que corresponde a C1 acrescido de 5,00% de juros, mas não tem sucesso nessa negociação inicial. O negociador resolve aplicar uma nova taxa sobre C2, mas sem ultrapassar a taxa anual máxima que está autorizado a oferecer. Qual o valor máximo da taxa a ser aplicada sobre C2?
(A) 2,16%
(B) 2,24%
(C) 3,20%
(D) 7,96%
(E) 16,72%
Resolução
Observe que o negociador oferece inicialmente um rendimento de 5%, ou seja, o capital do cliente, que antes era igual a C1, passaria a ser:
C2 = 1,05.C1
A questão informa que o cliente não aceitou a taxa ofertada e o negociador teve que aplicar uma nova taxa sobre C2. A nova taxa não pode ultrapassar a taxa máxima de 8,36%, ou seja, o capital C2 deve ser no máximo igual a 1,0836.C1.
Podemos calcular a taxa de crescimento do capital aplicado a uma taxa de 8,36% em relação ao capital aplicado a uma taxa de 5% da seguinte forma:
1,0836.C1 / 1,05.C1 = 1,0836/1,05 = 1,032
Veja que o capital cresceria a uma taxa de 1,032, ou seja, 3,2%.
Resposta: C
27. Um cliente montou uma estratégia financeira, aplicando parte de seu décimo terceiro salário, sempre no início de janeiro, de 2018 a 2021, conforme mostrado na Tabela a seguir.

A partir da orientação financeira de um especialista, ele conseguiu obter nesse período, com essas aplicações, uma taxa de retorno de 10% ao ano, sempre na comparação com o ano anterior. Ele pretende atingir o valor total acumulado de 65 mil reais no início de jan/2023. Considerando-se que essa taxa de retorno se mantenha, o valor mínimo, em reais, que esse cliente precisará depositar em Jan/2022, para atingir a meta em Jan/2023, a partir das aproximações dadas, pertence ao intervalo:
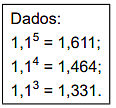
(A) R$ 8.000,00 a R$ 8.199,00
(B) R$ 8.200,00 a R$ 8.399,00
(C) R$ 8.400,00 a R$ 8.599,00
(D) R$ 8.600,00 a R$ 8.799,00
(E) R$ 8.800,00 a R$ 8.999,00
Resolução
Calcularemos o montante em cada um dos quatro depósitos apresentados na tabela.
Jan/2018 (prazo de 5 anos)
M = C.(1 + i)n
M = 10000.(1+0,1)5
M = 10000.1,15
M = 10000.1,611
M = 16110,00
Jan/2019 (prazo de 4 anos)
M = C.(1 + i)n
M = 10000.(1+0,1)4
M = 10000.1,14
M = 10000.1,464
M = 14640,00
Jan/2020 (prazo de 3 anos)
M = C.(1 + i)n
M = 10000.(1+0,1)3
M = 10000.1,13
M = 10000.1,331
M = 13310,00
Jan/2020 (prazo de 2 anos)
M = C.(1 + i)n
M = 10000.(1+0,1)2
M = 10000.1,12
M = 10000.1,21
M = 12100,00
Total: R$ 56.160,00
Como a meta do cliente é ter R$ 65.000,00 em jan/2023, então ele precisará de:
65000 – 56160 = R$ 8.840,00
Observe que o valor que será aplicado em jan/2022 deverá ser tal que, sob uma taxa de 10% a.a., tenha como resultado um montante de R$ 8.840,00.
x.1,1 = 8840
x = 8840 / 1,1
x = R$ 8.036,36
Resposta: A
28. Devido às oscilações de receita em seu negócio durante a pandemia, um cliente vai precisar pagar um boleto, cujo principal (até a data de vencimento) é de R$ 25.000,00, com 12 dias de atraso. Nesse caso, são cobrados adicionalmente, sobre o valor do principal, dois encargos: 2% de multa, mais juros simples de 0,2% ao dia. Por causa dos juros altos, o cliente procurou seu gerente, que não conseguiu uma solução menos custosa. Com isso, nas condições dadas, o cliente deverá pagar nessa operação um valor total de
(A) R$ 25.600,00
(B) R$ 25.800,00
(C) R$ 26.100,00
(D) R$ 26.300,00
(E) R$ 26.500,00
Resolução
Devemos calcular o valor da multa, que é fixa, independentemente do prazo de atraso, e dos juros simples, referentes a 12 dias.
Multa
25000 x 2% = 500,00
Juros Simples
J = C.i.t = 25000 . 0,002 . 12 = 600,00
Total
25000 + 500 + 600 = R$ 26.100,00
Resposta: C
29. Um cliente fez um investimento de R$ 100.000,00 em janeiro de 2019, comprando cotas de um fundo imobiliário, o que lhe proporcionou uma taxa de retorno de 21%, ao final de 12 meses de aplicação. Em janeiro de 2020, buscando maior rentabilidade, procurou um especialista financeiro indicado pelo seu gerente, que lhe recomendou aplicar todo o montante da operação anterior em renda variável. O cliente fez conforme recomendado, o que lhe proporcionou um retorno de 96% em 12 meses, resgatando o novo montante em janeiro de 2021. Considerando-se um sistema de juros compostos, a taxa de retorno equivalente, obtida em cada período de 12 meses pelo cliente, de janeiro de 2019 a janeiro de 2021, foi igual a
(A) 54%
(B) 56%
(C) 58%
(D) 60%
(E) 62%
Resolução
Aplicação em fundo imobiliário (21% a.a.)
100000 x 1,21 = R$ 121.000,00
Aplicação em renda variável (96% a.a.)
121000 x 1,96 = R$ 237.160,00
Observe que no período de janeiro de 2019 a janeiro de 2021, o capital, que era de 100 mil reais, passou a ser de R$ 237.160, em dois períodos de 12 meses.
Podemos calcular a taxa de retorno equivalente através da fórmula do montante para juros compostos:
M = C.(1 + i)n
237160 = 100000.(1 + i)2
(1 + i)2 = 237160/100000
(1 + i)² = 2,3716
1 + i = √2,3716
1 + i = 1,54
i = 1,54 – 1
i = 0,54 = 54%
Resposta: A
30. Devido à pandemia, um microempreendedor precisou tomar um empréstimo no valor de R$ 20.000,00, em dez/2020, a ser pago em 24 prestações mensais iguais e postecipadas no sistema PRICE, de modo que a primeira fosse paga em jan/21, e a última, em dez/22. Considere que o Banco cobre R$ 660,00 de taxas, que serão financiadas juntamente com o valor do empréstimo, por escolha do cliente, e que a taxa de juros cobrada, devido ao risco da operação, seja de 3% ao mês. Desconsiderando-se o IOF na operação e supondo-se que a primeira prestação foi paga na data de vencimento, o valor da segunda prestação, em sua respectiva data de vencimento será de, aproximadamente,
(A) R$ 1.120,00
(B) R$ 1.220,00
(C) R$ 1.320,00
(D) R$ 1.420,00
(E) R$ 1.520,00
Resolução
O sistema PRICE é aquele em que todas as prestações possuem o mesmo valor, ou seja, tanto faz calcular o valor da primeira, segunda ou terceira prestações.
Utilizaremos a fórmula do sistema PRICE, sabendo que:
PMT = prestação fixa
PV = valor presente = 20000 + 660 = 20660
i = taxa de juros mensal = 3% a.m.
n = prazo = 24 meses
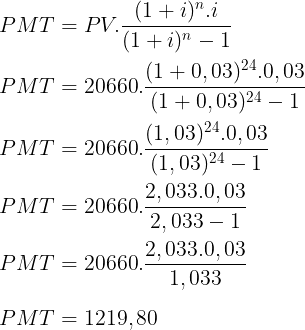
Resposta: B
Veja no Youtube:
Gostou da prova de matemática resolvida do concurso para o cargo de agente comercial do Banco do Brasil, organizado em 2021 pela Cesgranrio?
Deixe o seu comentário.
