Confira a prova resolvida do concurso para o Banco do Brasil (BB) realizado em 2014 pela Cesgranrio.

 

 

 

11. Uma empresa contraiu um financiamento para a aquisição de um terreno junto a uma instituição financeira, no valor de dois milhões de reais, a uma taxa de 10% a.a., para ser pago em 4 prestações anuais, sucessivas e postecipadas. A partir da previsão de receitas, o diretor financeiro propôs o seguinte plano de amortização da dívida:

Ano 1 – Amortização de 10% do valor do empréstimo;

Ano 2 – Amortização de 20% do valor do empréstimo;

Ano 3 – Amortização de 30% do valor do empréstimo;

Ano 4 – Amortização de 40% do valor do empréstimo.

Considerando as informações apresentadas, os valores, em milhares de reais, das prestações anuais, do primeiro ao quarto ano, são, respectivamente,

(A) 700, 650, 600 e 500

(B) 700, 600, 500 e 400

(C) 200, 400, 600 e 800

(D) 400, 560, 720 e 860

(E) 400, 580, 740 e 880

Ano 1:

Amortizou 10% do empréstimo de 2.000.000,00 (200.000,00)

Juros gerados: 10% de 2.000.000,00 = 200.000,00

Prestação: 200.000,00 + 200.000,00 = 400.000,00

Ano 2:

Amortizou 20% do empréstimo de 2.000.000,00 (400.000,00)

Juros gerados: 10% de 1.800.000,00 = 180.000,00

Prestação: 400.000,00 + 180.000,00 = 580.000,00

Ano 3:

Amortizou 30% do empréstimo de 2.000.000,00 (600.000,00)

Juros gerados: 10% de 1.400.000,00 = 140.000,00

Prestação: 600.000,00 + 140.000,00 = 740.000,00

Ano 4:

Amortizou 40% do empréstimo de 2.000.000,00 (800.000,00)

Juros gerados: 10% de 800.000,00 = 80.000,00

Prestação: 800.000,00 + 80.000,00 = 880.000,00

 

 

12. Um cliente contraiu um empréstimo, junto a um banco, no valor de R$ 20.000,00, a uma taxa de juros compostos de 4% ao mês, com prazo de 2 trimestres, contados a partir da liberação dos recursos. O cliente quitou a dívida exatamente no final do prazo determinado, não pagando nenhum valor antes disso. Qual o valor dos juros pagos pelo cliente na data da quitação dessa dívida? 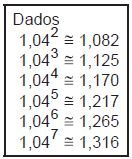(A) R$ 5.300,00

(B) R$ 2.650,00

(C) R$ 1.250,00

(D) R$ 1.640,00

(E) R$ 2.500,00

Tratando-se de juros compostos de 4% a.m. e considerando que a dívida foi paga após 6 meses, basta multiplicarmos o valor emprestado por 1,265 para descobrirmos o valor final (capital + juros).

Para calcularmos apenas os juros, basta multiplicarmos por 0,265: 20000 x 0,265 = 5.300

 

 

13. Uma empresa gera números que são chamados de protocolos de atendimento a clientes. Cada protocolo é formado por uma sequência de sete algarismos, sendo o último, que aparece separado dos seis primeiros por um hífen, chamado de dígito controlador. Se a sequência dos seis primeiros algarismos forma o número n, então o dígito controlador é o algarismo das unidades de n³ – n². Assim, no protocolo 897687 – d, o valor do dígito controlador d é o algarismo das unidades do número natural que é resultado da expressão 897687³ – 897687², ou seja, d é igual a

(A) 0

(B) 1

(C) 4

(D) 3

(E) 2

Calculando o algarismo das unidades de 897687³: 7x7x7 = 343 (algarismo 3)

Calculando o algarismo das unidades de 897687² 7×7 = 49 (algarismo 9)

A diferença entre 897687³ – 897687² só pode ter como algarismo da unidade o 4.

 

 

 

14. Durante 185 dias úteis, 5 funcionários de uma agência bancária participaram de um rodízio. Nesse rodízio, a cada dia, exatamente 4 dos 5 funcionários foram designados para trabalhar no setor X, e cada um dos 5 funcionários trabalhou no setor X o mesmo número N de dias úteis.O resto de N na divisão por 5 é

(A) 4

(B) 3

(C) 0

(D) 1

(E) 2

Note que cada funcionário trabalhará 185.4/5 = 148 dias

Como 145 é múltiplo de 5, o resto de 148 por 5 é 3.

 

 

15. Numa empresa, todos os seus clientes aderiram a apenas um dos seus dois planos, Alfa ou Beta. O total de clientes é de 1.260, dos quais apenas 15% são do Plano Beta. Se x clientes do plano Beta deixarem a empresa, apenas 10% dos clientes que nela permanecerem estarão no plano Beta. O valor de x é um múltiplo de

(A) 3

(B) 8

(C) 13

(D) 11

(E) 10

Clientes que aderiram ao plano Beta: 15% de 1260 = 1260.15/100 = 189

Clientes que aderiram ao plano Alfa: 1260 – 189 = 1071

Sabendo que se x pessoas do Beta deixarem a empresa, estes corresponderão a 10%:

(189 – x)/(1260 – x) = 0,10

189 – x = 0,1(1260 – x)

189 – x = 126 – 0,1x

x – 0,1x = 189 – 126

0,9x = 63

x = 63/0,9 = 70

Logo, x é múltiplo de 10

 

 

16. Apenas três equipes participaram de uma olimpíada estudantil: as equipes X, Y e Z. A Tabela a seguir apresenta o número de medalhas de ouro, de prata e de bronze obtidas por essas equipes. 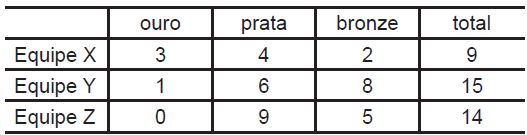De acordo com os critérios adotados nessa competição, cada medalha dá a equipe uma pontuação diferente: 4 pontos por cada medalha de ouro, 3 pontos por cada medalha de prata e 1 ponto por cada medalha de bronze. A classificação final das equipes é dada pela ordem decrescente da soma dos pontos de cada equipe, e a equipe que somar mais pontos ocupa o primeiro lugar. Qual foi a diferença entre as pontuações obtidas pelas equipes que ficaram em segundo e em terceiro lugares?

(A) 6

(B) 5

(C) 1

(D) 2

(E) 4

Equipe X: 3.4 + 4.3 + 2.1 = 12 + 12 + 2 = 26

Equipe Y: 1.4 + 6.3 + 8.1 = 4 + 18 + 8 = 30

Equipe Z: 0.4 + 9.3 + 5.1 = 0 + 27 + 5 = 32

Temos: 30 – 26 = 4

 

 

17. Em uma caixa há cartões. Em cada um dos cartões está escrito um múltiplo de 4 compreendido entre 22 e 82. Não há dois cartões com o mesmo número escrito, e a quantidade de cartões é a maior possível. Se forem retirados dessa caixa todos os cartões nos quais está escrito um múltiplo de 6 menor que 60, quantos cartões restarão na caixa?

(A) 12

(B) 11

(C) 3

(D) 5

(E) 10

Entre 1 e 82 temos 20 múltiplos de 4.

Entre 1 e 21 temos 5 múltiplos de 4.

Concluímos que entre 22 e 82 temos 15 múltiplos de 4.

Então temos 15 cartões pois é a “maior possível”.

Para retirarmos os múltiplos de 6, devemos retirar os múltiplos comuns de 4 e 6.

Temos que mmc(4,6) = 12

Os múltiplos de 12 são: 0, 12, 24, 48, 60, 84

Logo, retiramos as cartas de número 24, 48 e 60.

Restarão: 15 – 3 = 12 cartões

 

 

18. A variância de um conjunto de dados é 4 m². Para o mesmo conjunto de dados foram tomadas mais duas medidas de variabilidade:

a diferença entre o terceiro e o primeiro quartil e

o coeficiente de variação.

Esses dois valores caracterizam-se, respectivamente, por

(A) possuírem unidades de medida m² e m.

(B) possuírem unidades de medida m e m².

(C) ser adimensional e possuir unidade de medida m².

(D) possuir unidade de medida m e ser adimensional.

(E) possuir unidade de medida m² e ser adimensional.

Para calcularmos a variância, somamos todos os desvios de cada termo com a média, elevamos ao quadrado, e dividimos pelo número de dados. Logo, a variância é uma medida ao quadrado.

Daí podemos concluir que os termos serão em metros, pois a variância está em metros quadrados.

Como os quartis são medidas de posição então têm a unidade do dado da amostra (metros).

Já o coeficiente de variação não tem unidade, uma vez que é a divisão do desvio padrão pela média e essas duas medidas tem a mesma unidade de medida, logo é adimensional.

 

 

19. Considerando-se a mesma taxa de juros compostos, se é indiferente receber R$ 1.000,00 daqui a dois meses ou R$ 1.210,00 daqui a quatro meses, hoje, esse dinheiro vale

(A) R$ 909,09

(B) R$ 826,45

(C) R$ 466,51

(D) R$ 683,01

(E) R$ 790,00

Em dois meses, a taxa de crescimento (fator de capitalização) desse dinheiro é de:

1210/1000 = 1,21

Para calcularmos o valor do dinheiro hoje, como o período também é de dois meses:

1000/1,21 = 826,45

 

 

20. Sejam X o número de contratos realizados, e Y o número de contratos cancelados em uma determinada agência, por dia. A distribuição conjunta de X e Y é dada por

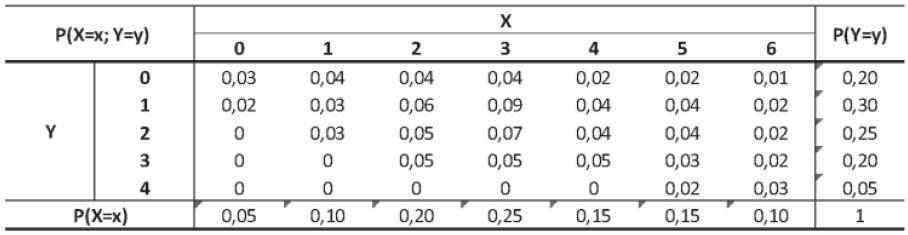Dado que pelo menos quatro contratos novos foram fechados, a probabilidade de que três contratos sejam cancelados no mesmo dia é:

a) 2/3

b) 1/3

c) 1/10

d) 1/8

e) 1/4

Pelo menos 4 contratos novos foram fechados, então podem ser 4 ou 5 ou 6:

0,15 + 0,15 + 0,1 = 0,4

Considerando as mesmas 3 colunas, a possibilidade de 3 cancelados é:

0,05 + 0,03 + 0,02 = 0,1

Calculando a probabilidade:

0,1 / 0,4 = 1/4