Confira aqui a prova resolvida do Banestes 2018, cargo de técnico bancário. O concurso foi organizado pela Fundação Getúlio Vargas (FGV).
Matemática e Raciocínio Lógico. Gabarito extraoficial em primeira mão!!!!!
Boa sorte!
MATEMÁTICA FINANCEIRA
Questão 21. Um contrato de empréstimo é firmado com taxa anual de juros de 24%, capitalizados trimestralmente sob regime de juros compostos.
A taxa semestral efetiva nessa contratação é:
a) 12,00%
b) 12,25%
c) 12,36%
d) 12,44%
e) 12,56%
Resolução
Considerando que a taxa de juros nominal é de 24% a.a., e que a capitalização é trimestral, utilizaremos a seguinte taxa proporcional:
24 / 4 = 6% ao trimestre = 0,06
Como queremos a taxa semestral efetiva, e em um semestre temos 2 trimestres, utilizaremos n = 2.
Te = (1 + i)n – 1
Te = (1 + 0,06)² – 1
Te = 1,06² – 1
Te = 1,1236 – 1
Te = 0,1236 = 12,36% ao semestre
Resposta: C
Questão 22. Caso certa dívida não seja paga na data do seu vencimento, sobre ela haverá a incidência de juros de 12% a.m.. Se essa dívida for quitada com menos de um mês de atraso, o regime utilizado será o de juros simples.
Considerando-se o mês comercial (30 dias), se o valor dessa dívida era R$ 3.000,00 no vencimento, para quitá-la com 8 dias de atraso, será preciso desembolsar:
a) R$ 3.096,00
b) R$ 3.144,00
c) R$ 3.192,00
d) R$ 3.200,00
e) R$ 3.252,00
Resolução
Como a dívida será paga com 8 dias de atraso, o regime será o de juros simples.
12% a.m. / 30 dias = 0,4% ao dia = 0,004
Utilizando a fórmula de juros simples:
M = C.(1 + in)
M = 3000.(1 + 0,004.8)
M = 3000.(1 + 0,032)
M = 3000.1,032
M = R$ 3.096,00
Resposta: A
Questão 23. O INPC (Índice Nacional de Preços ao Consumidor) é um indicador auferido mensalmente pelo IBGE que mede a variação de preços de um conjunto de produtos e serviços. Esse índice é utilizado pelo Governo como parâmetro para os reajustes de salários dos trabalhadores brasileiros.
Se, em determinado ano, o salário mínimo nacional for reajustado (aumentado) em 6,89%, e, nesse mesmo período, o INPC for de 5%, então o aumento real do poder de compra do salário mínimo será de:
a) 1,78%
b) 1,80%
c) 1,85%
d) 1,89%
e) 1,90%
Resolução
Considere (todas as taxas são anuais):
i (taxa aparente) = 6,89% = 0,0689
I (taxa de inflação) = 5% = 0,05
r (taxa real) = ?
Utilizando a fórmula do cálculo da taxa de juros real:
1 + i = (1 + I).(1 + r)
1 + 0,0689 = (1 + 0,05).(1 + r)
1,0689 = 1,05.(1 + r)
1 + r = 1,0689/1,05
1 + r = 1,018
r = 1,018 – 1
r = 0,018 = 1,80%
Resposta: B
Questão 24. Um equipamento eletrodoméstico custa R$ 175,00 à vista, mas pode ser adquirido a prazo por intermédio de três prestações antecipadas mensais iguais e consecutivas de R$ 100,00.
A taxa de juros efetiva composta ao mês cobrada nesse financiamento é de:
a) 100%
b) 80%
c) 75%
d) 72%
e) 36%
Resolução
A questão informa que são três prestações antecipadas, ou seja, uma das parcelas é considerada “entrada”.
Trazendo todas as prestações para o período zero:
175 = 100 + 100/(1+i) + 100/(1+i)²
100/(1+i) + 100/(1+i)² + 100 – 175 = 0
100/(1+i) + 100/(1+i)² – 75 = 0
Dividindo todos os termos por 25:
4/(1+i) + 4/(1+i)² – 3 = 0
Multiplicando todos os termos por (1+i)²:
4(1+i) + 4 – 3(1+i)² = 0
3(1+i)² – 4(1+i) – 4 = 0
Veja que temos uma equação do segundo grau, onde a incógnita é (1+i), com a=3, b=-4 e c=-4.
Resolvendo a referida equação (deixaremos a cargo do estudante), temos:
(1+i)’ = 2
(1+i)” = -0,66…
O único valor que nos interessa é o positivo:
1+i = 2
i = 2 – 1
i = 1 = 100%
Resposta: A
Questão 25. Um empréstimo deverá ser quitado em 6 prestações mensais iguais de R$ 670,00, segundo o Sistema de Amortização Francês (Tabela Price), com a primeira prestação vencendo um mês após a contratação. A taxa de juros nominal é de 60% ao ano, com capitalização mensal.
O saldo devedor imediatamente após o pagamento da 1ª prestação será:
Dado: 1,056 = 1,34
a) 2.900,00
b) 2.830,00
c) 2.800,00
d) 2.730,00
e) 2.700,00
Resolução
Como a taxa de juros nominal é de 60% a.a. e a capitalização é mensal, consideraremos a seguinte taxa mensal:
60% / 12 = 5% a.m. = 0,05
Calculando o valor financiado (PV), considerando que serão 6 prestações (n=6) mensais de 670 (PMT), com juros de 5% a.m. (i).
PV = PMT.[(1 + i)n – 1] / [(1 + i)n.i]
PV = 670.[(1 + 0,05)6 – 1] / [(1 + 0,05)6.0,05]
PV = 670.[(1,05)6 – 1] / [(1,05)6.0,05]
PV = 670.[1,34 – 1] / [1,34.0,05]
PV = 670.0,34 / 0,067
PV = 227,8 / 0,067
PV = 3400
Empréstimo no momento zero.
3400 = 670/1,05 + 670/1,05² + 670/1,05³ + 670/1,054 + 670/1,055 + 670/1,056
Após o pagamento da primeira prestação, restarão 5 prestações de 670, ou seja, o saldo devedor será de:
670/1,05 + 670/1,05² + 670/1,05³ + 670/1,054 + 670/1,055
Veja que o saldo devedor pode ser calculado efetuando a seguinte subtração:
3400 – 670/1,056
3400 – 670/1,34
3400 – 500
R$ 2.900,00
Resposta: A
Questão 26. Um título de valor nominal igual a R$ 12.000,00 sofre desconto comercial simples dois meses antes do seu vencimento.
Se a taxa de desconto é de 54% ao ano, o valor líquido recebido nessa operação corresponde a:
a) 1.080,00
b) 2.160,00
c) 5.520,00
d) 10.920,00
e) 11.460,00
Resolução
A taxa é anual e o desconto é mensal. Calculando a taxa proporcional:
54% a.a. / 12 = 4,5% a.m. = 0,045
O desconto comercial simples pode ser calculado através da seguinte fórmula:
d = N.i.n
Onde:
d = valor do desconto
N = valor nominal
i = taxa de juros
n = quantidade de períodos
d = N.i.n
d = 12000.0,045.2
d = 1080
Calculando o valor líquido recebido:
12000 – 1080 = 10.920
Resposta: D
Questão 27. Para adquirir um carro, Gabriel financiou o valor de R$ 36.000,00 a ser quitado em 120 prestações mensais e consecutivas. A primeira prestação, no valor de R$ 1.308,00, venceu um mês após a contratação do financiamento.
Se o sistema adotado foi o de Amortizações Constantes (SAC), a taxa de juros mensal efetiva aplicada a essa transação é:
a) 3%
b) 2,8%
c) 2,7%
d) 2,5%
e) 2,4%
O primeiro passo é calcular o valor das amortizações mensais:
36000 / 120 = 300
Veja que todos os meses Gabriel amortiza 300 reais, ou seja, o restante da prestação é referente a juros.
Calculando o valor dos juros na primeira prestação:
1308 – 300 = 1008
Como estamos na primeira parcela, os juros de R$ 1.008,00 foram calculados sobre o saldo devedor total, ou seja, sobre 36000.
1008 / 36000 = 0,028 = 2,8% a.m.
Resposta: B
Questão 28. Um título de crédito com valor nominal de R$ 9.000,00 foi descontado 20 dias antes do seu vencimento, segundo as regras do desconto bancário, à taxa simples de desconto de 6% ao mês.
Sobre essa operação, houve cobrança de IOF (Imposto sobre Operações Financeiras), com alíquota simples de 3% ao ano. Houve ainda a cobrança de uma taxa fixa de serviço bancário de 2%.
Sabendo-se que essas duas cobranças incidiram sobre o valor nominal do título, e considerando-se o ano comercial, o valor descontado foi:
a) 8.190,00
b) 8.437,00
c) 8.445,00
d) 8.485,50
e) 8.512,00
Resolução
Calculando todos os descontos:
- Taxa de serviço (taxa fixa de 2%):
9000 . 2% = 180
- IOF (alíquota simples de 3% a.a.)
Como a incidência será sobre 20 dias, e 360/20 = 18, temos:
9000.0,03/18 = 15
- Desconto (taxa simples de 6% a.m.)
6% a.m. = 0,2% a.d. = 0,002
d = N.i.n
d = 9000.0,002.20
d = 360
Somando o valor total dos descontos:
180 + 15 + 360 = 555
Valor líquido (valor descontado)
9000 – 555 = 8.445,00
Resposta: C
Questão 29. Uma carteira é formada exclusivamente por ações da VALE3 e da PETR4. Da quantidade total de ações dessa carteira, 75% correspondem a PETR4.
Novas ações da VALE3 foram adquiridas e incorporadas a essa carteira. Com isso, a quantidade de ações da VALE3 na carteira aumentou 50%.
Com relação à nova quantidade total de ações na carteira, as da PETR4 passaram a representar, aproximadamente?
a) 50%
b) 57%
c) 60%
d) 63%
e) 67%
Resolução
Para facilitar o nosso cálculo, consideraremos que a carteira era formada por 750 ações da PETR4 e 250 ações da VALE3.
Se a quantidade de ações da VALE3 aumentaram em 50%, a carteira passou a ter:
250.1,50 = 375
Composição da nova carteira:
750 ações da PETR4
375 ações da VALE3
Calculando a % de ações da PETR4:
750 / (750+375) = 750/1125 = 0,666… = 67%
Resposta: E
Questão 30. Antônia faz um empréstimo bancário de R$ 10.000,00, que será quitado em 5 prestações mensais antecipadas de R$ 1.400,00 cada uma e um pagamento final junto com a última prestação. O banco cobra juros efetivos de 7% a.m. sob regime de capitalização mensal composta e estipula um período de carência de dois meses.
O valor do pagamento final é:
Dado: 1,075 = 1,40
a) 69,80
b) 72,20
c) 722,00
d) 6.980,00
e) 7.220,00
Resolução
5 prestações mensais antecipadas e com carência de dois meses significa que a primeira parcela é imediata e a segunda é apenas após dois meses.
Como existe um pagamento final junto com a última prestação, consideraremos que este pagamento é igual a x. Veja que a última parcela será paga daqui a 5 meses.
Veja como ficam as prestações, trazendo para o período inicial:
10000 = 1400 + 1400/1,07² + 1400/1,07³ + 1400/1,074 + 1400/1,075 + x/1,075
10000 = 1400 + 1222,81 + 1142,81 + 1068,05 + 1000 + x/1,4
10000 = 5833,67 + x/1,4
x/1,4 = 10000 – 5833,67
x/1,4 = 4166,33
x = 4166,33 . 1,4
x = 5832,86
Calculando o valor do último pagamento:
1400 + 5832,86
7232,86 (valor aproximado)
Resposta: E
Questão 31. Uma duplicata tem valor nominal de R$ 4.000,00 e vencerá daqui a dois meses.
Se ela for descontada hoje pelas regras do desconto comercial composto, à taxa de desconto de 10% ao mês, o valor descontado será:
a) 760,00
b) 800,00
c) 2400,00
d) 3200,00
e) 3240,00
Resolução
Podemos calcular o desconto comercial composto através da seguinte fórmula:
A = N.(1 – i)n
Onde:
A = valor atual
N = valor nominal
i = taxa
n = prazo
A = N.(1 – i)n
A = 4000 . (1 – 0,1)2
A = 4000 . 0,9²
A = 4000 . 0,81
A = 3240
Resposta: E
Questão 32. Um capital de R$ 2.000,00 é aplicado a juros compostos de 10% ao mês. Depois de 3 meses de capitalização sem que houvesse qualquer retirada, o detentor desse montante faz um saque de R$ 562,00 e o restante do dinheiro continua a ser capitalizado nas mesmas condições.
Dois meses após essa retirada, o valor acumulado na aplicação é:
a) 2.466,00
b) 2.480,00
c) 2.500,00
d) 2.541,00
e) 2.626,00
Resolução
Calculando o rendimento após 3 meses, com taxa de 10% a.m. (0,1) e juros compostos:
M = C . (1 + i)n
M = 2000.(1 + 0,1)³
M = 2000.1,1³
M = 2000.1,331
M = 2662,00
Saldo após o saque de 562,00:
2662 – 562 = 2100
Calculando o rendimento após mais dois meses aplicados:
M = C . (1 + i)n
M = 2100.(1 + 0,1)²
M = 2100.1,1²
M = 2100.1,21
M = 2541,00
Resposta: D
Questão 33. Um capital de R$ 2.662,00 é capitalizado sob regime de juros compostos, ao longo de 4 meses, à taxa efetiva de 10% ao mês, produzindo um montante M.
Para que R$ 2.000,00 produzam o mesmo montante M, ele deve ser capitalizado nessas mesmas condições durante um período igual a:
a) 8 meses
b) 7 meses
c) 6 meses
d) 4 meses
e) 3 meses
Primeiro caso:
M = C . (1 + i)n
M = 2662 . (1 + 0,1)4
M = 2662 . 1,14
Segundo caso:
M = C . (1 + i)n
M = 2000 . (1 + 0,1)n
M = 2000 . 1,1n
Como o montante deve ser igual:
2000 . 1,1n = 2662 . 1,14
1,1n / 1,14 = 2662 / 2000
1,1n-4 = 1,331
1,1n-4 = 1,1³
n – 4 = 3
n = 3 + 4
n = 7 meses
Resposta: B
Questão 34. Um título foi descontado dois meses antes de seu vencimento, com taxa de desconto composto igual a 20% ao mês. Como o desconto foi comercial, o valor atual correspondeu a R$ 1.843,20.
Caso o desconto tivesse sido racional, o valor resgatado seria:
a) 1900
b) 1980
c) 2000
d) 2100
e) 2120
Resolução
Utilizando a fórmula de desconto comercial composto:
A = N.(1 – i)n
1843,2 = N . (1 – 0,2)²
1843,2 = N . 0,8²
1843,2 = N.0,64
N = 1843,2/0,64
N = 2880
Agora que encontramos o valor nominal do título, podemos utilizar a fórmula de desconto comercial composto:
N = A.(1 + i)n
2880 = A . (1 + 0,2)²
2880 = A.1,2²
2880 = A.1,44
A = 2880 / 1,44
A = 2000
Resposta: C
Questão 35. Em um terminal de autoatendimento bancário há apenas cédulas de R$ 10,00, R$ 20,00 e R$ 50,00.
As quantidades de cada um dos três tipos de cédula na máquina são inversamente proporcionais aos seus valores.
Se há 272 cédulas ao todo, então a quantidade total de dinheiro armazenado no terminal é:
a) 3600
b) 3960
c) 4050
d) 4240
e) 4800
Resolução
Sabendo que a quantidade de cada uma das notas é inversamente proporcional aos seus valores temos:
Quantidade de cédulas de R$ 10
x/10
Quantidade de cédulas de R$ 20
x/20
Quantidade de cédulas de R$ 50
x/50
Como existem 272 cédulas:
x/10 + x/20 + x/50 = 272
(10x + 5x + 2x)/100 = 272
17x = 272.100
17x = 27200
x = 27200/17
x = 1600
Quantidade de cédulas de R$ 10
x/10 = 1600/10 = 160
Quantidade de cédulas de R$ 20
x/20 = 1600/20 = 80
Quantidade de cédulas de R$ 50
x/50 = 1600/50 = 32
Total de dinheiro armazenado:
10.160 + 20.80 + 50.32 = 1600 + 1600 + 1600 = 4800
Resposta: E
Questão 36. Maria comprou duas bicicletas iguais, pagando R$ 360,00 em cada uma delas. Algum tempo depois, vendeu ambas: uma com lucro de 10% sobre o preço de venda e a outra com 15% de prejuízo sobre o preço de compra.
Nessa transação de compra e venda das bicicletas, Maria:
a) teve lucro de aproximadamente 2%
b) teve lucro de exatamente 5%
c) não teve lucro e nem prejuízo
d) teve prejuízo de exatamente 5%
e) teve prejuízo de aproximadamente 2%
Calculando o valor da venda da primeira bicicleta, considerando um lucro de 10% sobre o preço de venda:
360/0,9 = 400
Calculando o preço de venda da segunda bicicleta, considerando um prejuízo de 15% sobre o preço de compra:
360.0,85 = 306
Valor gasto: 360 + 360 = 720
Valor arrecadado: 400 + 306 = 706
Prejuízo: 720 – 706 = 14
Prejuízo percentual: 14/720 = 0,019 ≈ 2%
Resposta: E
Questão 37. Alberto aplicou um capital C da seguinte forma:
a) 40% de C em papéis de Renda Fixa (RF)
b) 60% de C em Letra de Crédito Imobiliário (LCI)
Ao longo de um ano, nenhum novo depósito foi feito em qualquer das duas modalidades de aplicação. Nesse mesmo período, não houve resgate.
Se as taxas efetivas de rendimento da RF e da LCI, no período referido, foram de 15% a.a. e 10% a.a., respectivamente, então essa estratégia conjunta de aplicação possibilitou a Alberto uma rentabilidade total sobre o capital C de:
a) 25%
b) 19%
c) 15%
d) 12%
e) 5%
Resolução
Podemos facilitar a resolução imaginando que o capital é igual a 100 reais.
RF (40 reais)
40 . 1,15 = 46
LCI (60 reais)
60 . 1,1 = 66
Total: 46 + 66 = 112
Claramente, o rendimento foi de 12%.
Resposta: D
Questão 38. Um financiamento no valor de R$ 8.000,00 foi contratado e deverá ser quitado em 5 prestações mensais e consecutivas, vencendo a primeira delas um mês após a data da contratação do financiamento. Foi adotado o Sistema de Amortização Constante (SAC) a uma taxa de juros efetiva de 4,5% ao mês.
O valor da 2ª prestação será:
a) 1.960
b) 1.888
c) 1.816
d) 1.744
e) 1.672
Resolução
Valor da amortização mensal:
8000 / 5 = 1600
Saldo devedor no pagamento da 2ª prestação:
8000 – 1600 = 6400
Valor da 2ª parcela:
1600 + 6400.4,5%
1600 + 288
1888
Resposta: B
Questão 39. João recebeu sua fatura do cartão de crédito no valor de R$ 4.000 e, no dia do vencimento, pagou o valor mínimo exigido (que corresponde a 15% do valor total). O restante foi quitado um mês depois.
Se a administradora do cartão de João cobra juros de 216% ao ano com capitalização mensal, sob regime de juros compostos, então o valor pago no ato da liquidação da dívida foi:
a) 4000
b) 4012
c) 4100
d) 4120
e) 4230
Resolução
Valor pago por João:
4000 . 15% = 600
Valor financiado:
4000 – 600 = 3400
Calculando a taxa de juros proporcional mensal:
216% a.a. / 12 meses = 18% a.m.
Como ele quitou um mês depois:
M = 3400.1,18 = 4012
Resposta: B
Questão 40. A tabela a seguir apresenta alguns resultados aproximados para 1,07n em função de n.
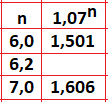
Ainda que as potências não aumentem de forma linear, é possível obter uma boa aproximação para 1,076,2 por meio de regra de três aplicada sobre intervalos entre valores apresentados.
Aplicando-se essa técnica, a aproximação obtida é:
a) 1,508
b) 1,510
c) 1,522
d) 1,530
e) 1,535
Resolução
O primeiro passo é dividir o intervalo de 6,0 a 7,0 em 10 partes.
Na primeira coluna teremos os seguintes valores: 6,0; 6,1; 6,2; 6,3…
Na segunda coluna teremos:
(1,606 – 1,501)/10 = 0,0105
Para n = 6,2, basta somarmos duas vezes o valor 0,0105:
1,076,2= 1,501 + 0,0105 + 0,0105 = 1,522
Resposta: C
RACIOCÍNIO LÓGICO
Questão 41. Considere a afirmação:
“João não trabalha e Maria fica em casa”
A negação dessa afirmação é:
a) João não trabalha e Maria não fica em casa
b) João trabalha e Maria fica em casa
c) João trabalha e Maria não fica em casa
d) João trabalha ou Maria não fica em casa
e) João trabalha ou Maria fica em casa
Resolução
Considerando a afirmação como P∧Q, onde:
P: João não trabalha
Q: Maria fica em casa
Quem estudou as leis de Morgan viu que a negação da conjunção P∧Q é a disjunção ~P∨~Q.
~P∨~Q: João trabalha ou Maria não fica em casa
Resposta: D
Questão 42. Em uma corrida de carros os pilotos X e Y largaram em 5º e 7º lugares, respectivamente. Durante a corrida, X fez duas ultrapassagens, depois Y fez 4 ultrapassagens e, em seguida, X fez três ultrapassagens. Não houve nenhuma ultrapassagem por parte dos outros pilotos e a corrida terminou.
Considere as afirmativas:
- X ganhou a corrida
- Y chegou em 4º
- Quem largou em 3º chegou em 5º
- Quem largou em 2º chegou na mesma posição
É/são verdadeira(s):
a) nenhuma
b) apenas uma
c) apenas duas
d) apenas três
e) todas
Resolução
- Posições iniciais:
X largou em 5º
Y largou em 7º
- Após duas ultrapassagens de X:
X: 3º
Y: 7º
- Após 4 ultrapassagens de Y:
X: 4º
Y: 3º
- Após 3 ultrapassagens de X:
X: 1º
Y: 4º
Veja que as duas primeiras afirmações são verdadeiras.
Quem largou em 3º chegou em 5º também é verdade, pois o terceiro foi ultrapassado por X e Y, ficando em 5º.
Quem largou em 2º chegou na mesma posição é falso, pois o 2º foi ultrapassado por X, ficando em 3º.
Resposta: D
Questão 43. Três pessoas com idades de 30, 40 e 50 anos estão sentadas em três poltronas, uma ao lado da outra, como na figura. Uma poltrona é preta, outra é azul e outra é marrom.
Sabe-se que:
- A pessoa mais velha não está na poltrona preta
- A pessoa da poltrona do meio é mais jovem que a da poltrona da direita
- A poltrona marrom está à direita da ocupada pela pessoa mais velha.
É correto concluir que:
a) a poltrona do meio está ocupada pela pessoa de 40 anos
b) a poltrona azul está imediatamente à esquerda da preta
c) a pessoa mais jovem está na poltrona marrom
d) a pessoa de 40 anos é vizinha da que está na poltrona azul
e) a poltrona preta é a do meio
Resolução
A dica para resolver este tipo de questão é montar uma tabela no formato abaixo.
Basta agora preencher com os dados informados. Veja, por exemplo, como deve ser preenchida com a primeira informação:
Preenchendo com todas as informações:
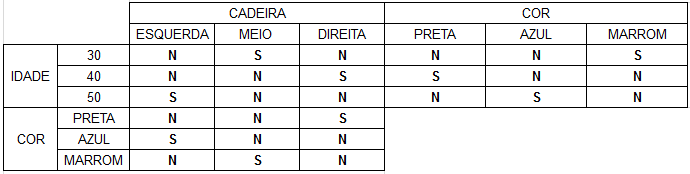
Resposta: C
Questão 44. 1 cm³ de gesso tem 1,4 g de massa.
A massa de 1 m³ de gesso é:
a) 1,4 kg
b) 14 kg
c) 140 kg
d) 1400 kg
e) 14000 kg
Resolução
Calculando quantos cm³ existem em 1 m³:
100.100.100 = 1000000 cm³
Usando a proporção informada:
1000000 . 1,4 = 1400000 g
Como 1 kg equivale a 1000 gramas:
1400000 = 1400 kg
Resposta: D
Questão 45. Mário, que mora em Vitória, está reunido com os amigos Fábio, Hélio e Sérgio, sentados em volta de uma mesa quadrada. Entre os seus amigos, um mora em Guarapari, outro em Colatina e outro em Linhares. Sabe-se que:
- Fábio está à direita de Mário
- Hélio está à direita de quem mora em Guarapari
- Sérgio não mora em Colatina e está em frente a Fábio
É correto concluir que:
a) Fábio mora em Guarapari e Sérgio em Linhares
b) Fábio mora em Colatina e Sérgio em Linhares
c) Fábio mora em Linhares e Sérgio em Guarapari
d) Hélio mora em Colatina e Sérgio em Guarapari
e) Hélio mora em Linhares e Sérgio em Guarapari
Resolução
Enumerando as posições ao redor da mesa, temos:
Vamos fixar Fábio na posição 1. Assim, Mário está na posição 2.
Sérgio está em frente à Fábio, ou seja, na posição 3, e Hélio na posição 4.
Hélio está à direita de Fábio. Daí, Fábio mora em Guarapari.
Se Sérgio não mora em Colatina, ele deve morar em Linhares, restando para Hélio a cidade de Colatina.
Resposta: A
Questão 46. Em certa empresa são verdadeiras as afirmações:
- Qualquer gerente é mulher.
- Nenhuma mulher sabe trocar uma lâmpada
É correto concluir que, nessa empresa:
a) algum gerente é homem
b) há gerente que sabe trocar uma lâmpada
c) todo homem sabe trocar uma lâmpada
d) todas as mulheres são gerentes
e) nenhum gerente sabe trocar uma lâmpada
Resolução
A primeira afirmação é equivalente a dizer que “todos os gerentes são mulheres”. Se nenhuma mulher sabe trocar uma lâmpada, podemos concluir que nenhum gerente sabe trocar lâmpada.
Resposta: E
Questão 47. Maria e Joana começaram, no mesmo dia, a ler um livro com 300 páginas. Maria lê 12 páginas por dia e Joana lê 15 páginas por dia.
Quando Joana terminar o livro, o número de páginas que Maria ainda terá para ler é:
a) 75
b) 60
c) 48
d) 45
e) 36
Resolução
Calculando a quantidade de dias gastos por Joana:
300 / 15 = 20 dias
Em 20 dias Maria terá lido:
12 . 20 = 240 páginas
Diferença:
300 – 240 = 60 páginas
Resposta: B
Questão 48. Considere a afirmação:
“Quem rouba é preso”
A negação dessa afirmação é:
a) alguém rouba e não é preso
b) quem não é preso não roubou
c) quem não rouba não é preso
d) quem rouba não é preso
e) alguém não rouba ou não é preso
Resolução
Podemos analisar a afirmação como uma condicional P⇒Q, cuja negação é P∧~Q, ou seja,
“Alguém rouba e não é preso”
Resposta: A
Questão 49. Para montar certo aparelho um operário demora 25 minutos.
Trabalhando continuamente, para montar 10 aparelhos esse operário gastará:
a) 4 horas
b) 4 horas e 10 minutos
c) 4 horas e 20 minutos
d) 4 horas e meia
e) 4 horas e 40 minutos
Resolução
Minutos gastos para montar 10 aparelhos:
25 minutos x 10 aparelhos = 250 minutos
250 = 4.60 + 10
4 horas e 10 minutos
Resposta: B
Questão 50. Em uma população de mosquitos, 70% são transmissores do vírus da dengue e os outros não. Dos mosquitos transmissores, 40% estão infectados com o vírus da dengue e os outros não.
Nessa população de mosquitos, os que não transmitem o vírus da dengue são:
a) 30%
b) 42%
c) 60%
d) 64%
e) 72%
Resolução
Um mosquito tem apenas duas opções: ele transmite ou não transmite o vírus da dengue.
Os mosquitos que transmitem o vírus são os que são transmissores e estão infectados:
70% . 40% = 28%
Concluindo, não transmitem o vírus:
100% – 28% = 72%
Resposta: E
Gostou da prova resolvida do Banestes 2018?
Deixe o seu comentário.

Gostei muito das resoluções! top, quero mais!
gostei muito das resoluções, doida pra ver o restante.
PENSEI QUE A ÚLTIMA FOSSE 30 LETRA A!!!
tó tentando descobrir ainda com x/10 * x/20 * x/50 virou 10x *5x * 2x quem souber me fala