Estudando matemática para concursos? Confira aqui a prova resolvida do concurso para o Banco da Amazônia (BASA), realizado em 2018 pela Cesgranrio.
Veja também em nosso menu outras provas resolvidas de carreiras bancárias e organizadas pela Cesgranrio.
Bom estudo!
Questão 6. O comprimento de um grande fio corresponde à soma dos comprimentos de 24 fios menores. São eles:
• 12 fios, cada um dos quais com comprimento que mede 14,7 cm;
• 4 fios, cada um dos quais com comprimento que mede 0,3765 km;
• 8 fios, cada um dos quais com comprimento que mede 13,125 dam.
Esse grande fio foi dividido em 3 fios de igual comprimento, chamados de unidade modelo. Qual é a medida, em metros, do comprimento de uma unidade modelo?
(A) 6385,500
(B) 2557,764
(C) 852,588
(D) 94,302
(E) 31,434
Resolução
12 fios de comprimento 14,7 cm:
12 . 14,7 = 176,4 cm = 1,764 m
4 fios de comprimento 0,3765 km:
4 . 0,3765 = 1,506 km = 1506 m
8 fios de comprimento 13,125 dam:
8 . 13,125 = 105 dam = 1050 m
Total:
1,764 + 1506 + 1050 = 2557,764 m
Dividindo o fio grande por 3:
2557,764 = 852,588
Resposta: C
Questão 7. Considere a sequência numérica cujo termo geral é dado por an=21-3n, para n ≥ 1. Essa sequência numérica é uma progressão
(A) geométrica, cuja razão é -3.
(B) aritmética, cuja razão é 1/8.
(C) geométrica, cuja razão é 1/8.
(D) geométrica, cuja razão é -6.
(E) aritmética, cuja razão é -3.
Resolução
Calculando os primeiros termos da sequência numérica:
a1 = 21-3.1 = 2-2 = 1/4
a2 = 21-3.2 = 2-5 = 1/32
a3 = 21-3.3 = 2-8 = 1/256
Dividindo dois termos consecutivos temos:
a2/a1 = (1/256) / (1/32) = 32/256 = 1/8
a3/a2 = (1/32) / (1/4) = 4/32 = 1/8
Mas será que é sempre igual a 1/8?
Vamos generalizar:
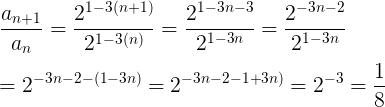
Veja que não importa os termos, a divisão entre dois consecutivos é sempre igual a 1/8, ou seja, temos uma progressão geométrica de razão 1/8.
Resposta: C
Questão 8. Um valor inicial C0 foi capitalizado por meio da incidência de juros compostos mensais constantes iguais a 6,09%. Ao final de 6 meses, isto é, após 6 incidências dos juros, gerou-se o montante M.
A partir do valor inicial C0, seria alcançado o mesmo montante M ao final de 12 meses (12 incidências), se os juros compostos mensais constantes tivessem sido iguais a
(A) 1,045%
(B) 1,450%
(C) 3,045%
(D) 3,450%
(E) 3,000%
Resolução
Utilizando a fórmula de juros compostos para n = 6 meses e i = 0,0609 (6,09% ao mês), temos:
M = C . (1 + i)n
M = C0 . (1 + 0,0609)6
M = C0 . 1,06096
Utilizando a mesma fórmula, agora para n = 12 meses, e taxa igual a j (ao mês).
M = C0 . (1 + j)12
Igualando as expressões:
C0 . 1,06096 = C0 . (1 + j)12
1,06096 =(1 + j)12
Tirando a raiz sexta em ambos os lados:
1,0609 = (1+j)²
1,03 = 1 + j
j = 1,03 – 1
j = 0,03 = 3% a.m.
Resposta: E
Questão 9. Sabe-se que 30% dos clientes de um banco são do sexo masculino e os 70% restantes são do sexo feminino. Entre os clientes do sexo masculino, a média do tempo de vínculo com o banco é igual a 4 anos e, entre os clientes do sexo feminino, é igual a 6 anos.
Considerando-se todos os clientes, de ambos os sexos, qual é a média do tempo de vínculo de cada um com o banco?
(A) 5 anos
(B) 5,3 anos
(C) 6 anos
(D) 5,4 anos
(E) 5,7 anos
Resolução
Neste caso devemos calcular a média ponderada. Veja:
Média = (4.30 + 6.70)/100
Média = (120 + 420)/100
Média = 540/100
Média = 5,4 anos
Resposta: D
Questão 10. No conjunto dos números reais, considere as seguintes duas inequações:
Inequação 1: 5x – 7 > x² – x + 1
Inequação 2: x + 6 > -x + 10
Um número real x, que é solução da inequação 2, também será solução da inequação 1, se, e somente se, for solução da inequação
(A) x² – 16 > 0
(B) 1/x < 1/4
(C) -x < -4
(D) 4x – 16 < 0
(E) x + 1 > x + 9
Resolução
Resolvendo a primeira inequação:
5x – 7 > x² – x + 1
x² – x + 1 – 5x + 7 < 0
x² – 6x + 8 < 0
Utilizaremos agora o método da soma e do produto para encontrarmos as raízes da equação x² – 6x + 8 = 0.
S = -b/a = -(-6)/1 = 6
P = c/a = 8/1 = 8
Os dois valores cuja soma é igual a 6 e o produto é igual a 8 são 2 e 4.
O gráfico da função x² – 6x + 8 é uma parábola com concavidade para cima. Ela será negativa apenas no intervalo ]2, 4[.
Resolvendo a segunda inequação:
x + 6 > -x + 10
2x – 4 > 0
x > 2
Analisando os valores de x que atendem a inequação 2, eles também atenderão a inequação 1 se forem menores que 4, ou seja, x < 4, que é equivalente a inequação:
4x – 16 < 0
Resposta: D
Gostou da prova resolvida do Banco da Amazônia (BASA) 2018?
Deixe o seu comentário.
