Estudando matemática e raciocínio lógico para concursos? Confira aqui a prova resolvida do concurso ABIN 2018, realizado pelo CESPE.
Veja também em nosso site as nossas provas resolvidas de outros concursos do CESPE e de outras bancas.
Bom estudo!
A sequência infinita: a0, a1, a2, a3, … é definida por: a0 = 1, a1 = 3 e, para cada número inteiro n≥1, a2n = a2n-1 + a2n-2, e a2n+1 = a2n – a2n-1. Com relação a essa sequência, julgue os itens seguintes.
55 A soma a10 + a9 é superior a 20.
Resolução
Veja que temos uma sequência infinita de termos, onde já sabemos os termos a0 e a1, e os demais podem ser calculados pela seguintes regras:
- Cada termo de índice par é a soma dos dois anteriores;
- Cada termo de índice ímpar é a subtração dos dois anteriores.
Escrevendo a sequência:
a0 = 1
a1 = 3
a2 = 4
a3 = 1
a4 = 5
a5 = 4
a6 = 9
a7 = 5
a8 = 14
a9 = 9
a10 = 23
a11 = 14
…
a10 + a9 = 23 + 9 = 32
Resposta: CERTO
56 Existem infinitos valores inteiros de p e q tais que ap = aq.
Resolução
Veja que o formato de construção da sequência faz com que um termo seja sempre igual ao terceiro termo anterior, ou ao terceiro termo subsequente, ou seja, teremos infinitos casos onde teremos dois termos iguais. A única exceção é o termo a1.
Resposta: CERTO
Como forma de melhorar a convivência, as famílias Turing, Russell e Gödel disputaram, no parque da cidade, em um domingo à tarde, partidas de futebol e de vôlei. O quadro a seguir mostra os quantitativos de membros de cada família presentes no parque, distribuídos por gênero.
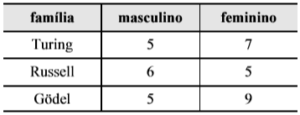
A partir dessa tabela, julgue os itens subsequentes.
57 A quantidade de maneiras distintas de se formar um time de vôlei com seis integrantes, sendo três homens da família Turing e três mulheres da família Gödel, é superior a 700.
Resolução
Como não existe ordem, basta combinar os 5 homens da família Turing em grupos de 3, e as 9 mulheres da família Godel em grupos de 3:
C5,3 = 5!/3!2! = 10
C9,3 = 9!/3!6! = 84
Total: 10 . 84 = 840
Resposta: CERTO
58 Considere que, em eventual sorteio de brindes, um nome tenha sido retirado, ao acaso, do interior de uma urna que continha os nomes de todos os familiares presentes no evento. Nessa situação, sabendo-se que o sorteado não é uma mulher da família Gödel, a probabilidade de ser uma mulher da família Russel será superior a 20%.
Resolução
Existem 5 mulheres na família Russel.
O total de pessoas é 37, porém 9 são mulheres da família Godel, ou seja, temos 28 possibilidades.
P = 5/28 = 0,178 = 17,8%
Resposta: ERRADO
Julgue os itens a seguir, a respeito de lógica proposicional.
59 A proposição “Os Poderes Executivo, Legislativo e Judiciário devem estar em constante estado de alerta sobre as ações das agências de inteligência.” pode ser corretamente representada pela expressão lógica P∧Q∧R, em que P, Q e R são proposições simples adequadamente escolhidas.
Resolução
Temos aqui uma proposição simples, e não uma proposição composta.
Resposta: ERRADO
60 A proposição “A vigilância dos cidadãos exercida pelo Estado é consequência da radicalização da sociedade civil em suas posições políticas.” pode ser corretamente representada pela expressão lógica P⇒Q, em que P e Q são proposições simples escolhidas adequadamente.
Resolução
Da mesma forma que a questão anterior, temos uma proposição simples, e não composta.
Resposta: ERRADO
Gostou da prova resolvida da ABIN 2018?
Deixe o seu comentário.
