Confira aqui a prova de matemática comentada do ENEM 2018 (caderno rosa).

O Exame Nacional do Ensino Médio é a mais importante prova do país, e conta anualmente com a participação de milhões de estudantes de todo o Brasil.

Boa sorte!

Resolução

O enunciado informa que a força gravitacional F é proporcional à massa m e inversamente proporcional ao quadrado do raio da órbita. Analisando a fórmula, o correto seria ter informado que “a força gravitacional F é diretamente proporcional à massa m”. Não acredito que a questão será anulada por este motivo, considerando que isto pode ser deduzido pela fórmula, mas vale o registro.

Comparando as forças dos satélites A e B:

O raio de A é igual ao raio de B, enquanto a massa de B é maior que a massa de A.

Como a força é diretamente proporcional à massa, e os raios são iguais, podemos concluir que a força do satélite de maior massa é maior, ou seja, F_B>F_A.

Comparando as forças dos satélites A e C:

O raio de C é maior que o raio de A, enquanto a massa de C é igual à massa de A.

Como a força é inversamente proporcional ao quadrado do raio, e as massas são iguais, podemos concluir que a força do satélite de menor raio é maior, ou seja, F_A>F_C.

Como F_B>F_A e F_A>F_C, temos que F_B>F_A>F_C.

Resposta: E

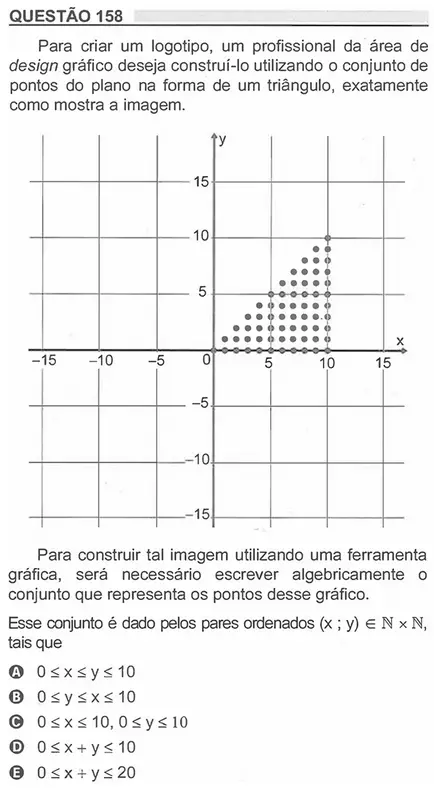
Questão 137. Os tipos de prata normalmente vendidos são 975, 950 e 925. Essa classificação é feita de acordo com a sua pureza. Por exemplo, a prata 975 é a substância constituída de 975 partes de prata pura e 25 partes de cobre em 1 000 partes da substância. Já a prata 950 é constituída de 950 partes de prata pura e 50 de cobre eco 1000; e a prata 925 é constituída de 925 partes de prata pura e 75 partes de cobre em 1 000. Um ourives possui 10 gramas de prata 925 e deseja obter 40 gramas de prata 950 para produção de uma joia.

Nessas condições, quantos gramas de prata e de cobre, respectivamente, devem ser fundidos com os 10 gramas de prata 925?

a) 29,25 e 0,75

b) 28,75 e 1,25

c) 28,50 e 1,50

d) 27,75 e 2,25

e) 25,00 e 5,00

Resolução

O ourives possui 10 gramas da prata 925, que é composta por prata pura (92,5%) e cobre (7,5%).

Separando a prata pura do cobre, ele possui:

10 . 92,5% = 9,25 gramas de prata pura

10 . 7,5% = 0,75 gramas de cobre

Ele deseja obter 40 gramas de prata 950, que é composta por prata pura (95%) e cobre (5%).

Calculando a quantidade de cada um dos elementos necessários para fabricar 40 gramas de prata 950:

40 . 95% = 38 gramas de prata pura

40 . 5% = 2 gramas de cobre

Calculando a quantidade a ser acrescentada:

Prata pura: 38 – 9,25 = 28,75 gramas

Cobre: 2 – 0,75 = 1,25 gramas

Resposta: B

Resolução

A figura informa para cada uma das 5 máquinas o tempo gasto com cada passageiro e a quantidade de pessoas na fila.

Calcularemos o tempo gasto em cada uma das filas:

Máquina 1

35 . 5 = 175 segundos

Máquina 2

25 . 6 = 150 segundos

Máquina 3

22 . 7 = 154 segundos

Máquina 4

40 . 4 = 160 segundos

Máquina 5

20 . 8 = 160 segundos

O passageiro gastará o menor tempo (150 segundos) na máquina 2.

Resposta: B

Resolução

Como a tabela apresenta a quantidade de trabalhadores que sofreram certa quantidade de acidentes, basta calcularmos a média ponderada.

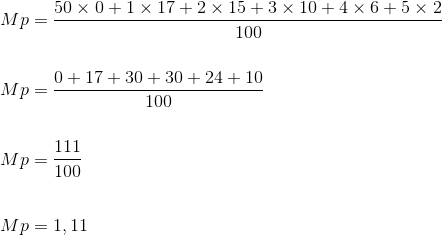
Resposta: D

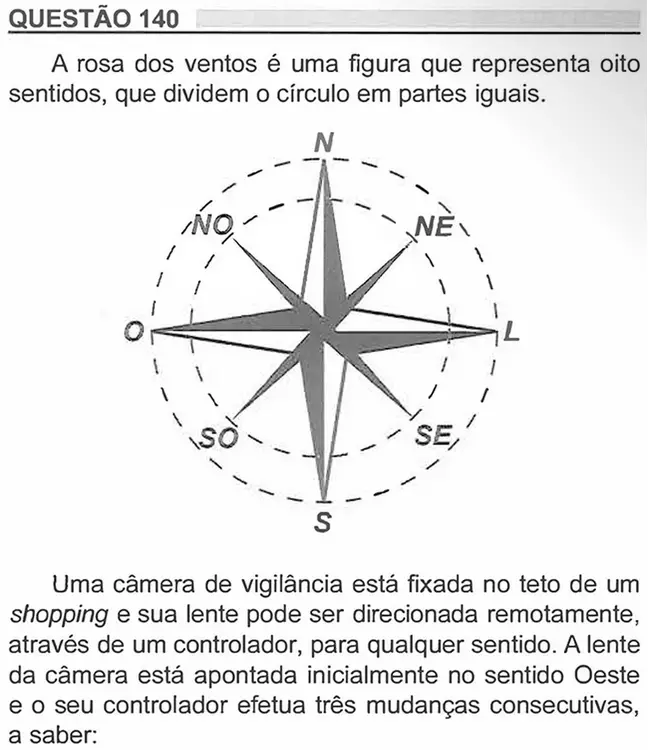
Vamos considerar que todas as mudanças no sentido anti-horário são negativas, e todas as mudanças no sentido horário são positivas.

1ª mudança: – 135º

2ª mudança: 60º

3ª mudança: – 45º

Somando todas as mudanças:

– 135º + 60º – 45º = – 120º

Veja que ao final das três mudanças, a câmera ficou posicionada a 120º no sentido anti-horário.

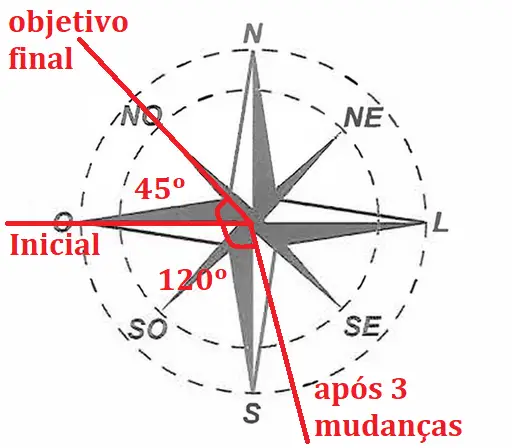
Após as 3 mudanças, o controlador deve reposicionar a câmera no sentido Noroeste com a menor amplitude possível, ou seja, utilizando o menor caminho.

Pela figura é fácil perceber que ele deve voltar os 120º no sentido horário, passando pelo ponto inicial, e que está a 45º do objetivo final.

Total: 120º + 45º = 165º

Resposta: E

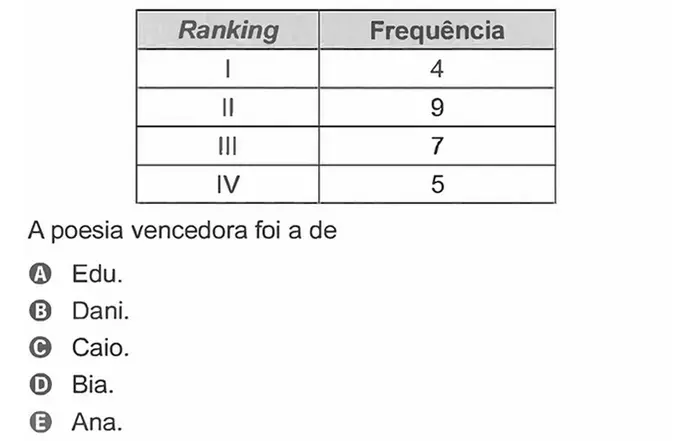
Resolução

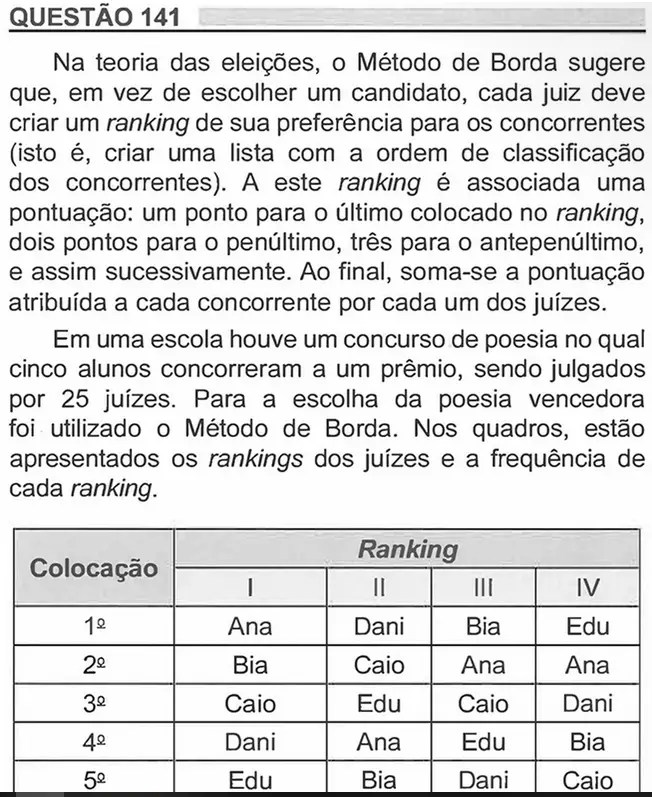
Analisando as tabelas acima, podemos concluir que os 25 juízes escolheram 4 rankings, sendo que na tabela 2 temos a quantidade de vezes que cada ranking foi escolhido.

Sabendo que o primeiro colocado em cada ranking recebe 5 pontos, o segundo recebe 4, e assim sucessivamente, calcularemos a pontuação de cada um dos concorrentes.

Veja na tabela que Ana alcançou a maior pontuação.

Resposta: E

Resolução

Faremos a viagem da criança de trás para frente.

Ela parou no quinto andar após descer 4 andares, ou seja, ele veio do nono andar.

Ela parou no nono andar após subir 9 andares, ou seja, ele veio do térreo.

Ela parou no térreo após descer 10 e depois mais 13 andares, ou seja, ele veio do vigésimo terceiro andar.

Ela parou no 23º andar após subir 7 andares em relação ao andar inicial, ou seja, ele veio do 16º andar.

Como a questão informa que o elevador parou uma vez no último andar, podemos concluir que este prédio possui 23 andares.

Resposta: C

Resolução

Temos dois estandes, onde serão expostos um carro compacto e uma caminhonete em cada um deles, sendo que existem 4 carros compactos e 6 caminhonetes diferentes.

O primeiro passo será escolher 2 carros compactos entre os 4 possíveis. Temos aqui uma combinação de 4, tomados 2 a 2, ou seja, a quantidade é igual a C_4,2. Como são dois estandes, temos duas opções para os carros escolhidos. Total de opções:

2 . C_4,2

O segundo passo será escolher 2 caminhonetes entre os 6 possíveis. Temos novamente uma combinação, porém de 6, tomados 2 a 2, ou seja, C_6,2. Como são dois estandes, também multiplicaremos por 2:

2 . C_6,2

Total de maneiras diferentes:

C_4,2 . C_6,2 . 2 . 2

Resposta: C

Resolução

Perceba que cada uma das provas tem um “peso” diferente. Podemos resolver a questão utilizando os conceitos de média ponderada, onde consideraremos que x é a nota que o aluno deve obter na quarta prova, de modo que consiga atingir a média mínima de 60 pontos.

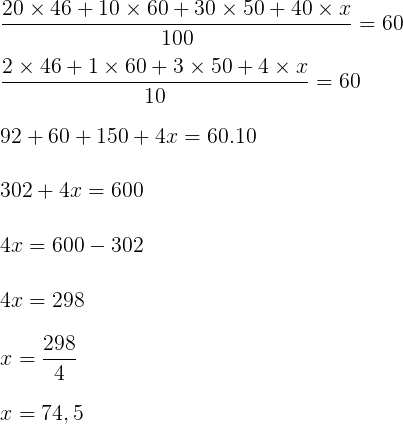
Resposta: C

Resolução

O gerente acrescentou inicialmente 20 perguntas, sendo que 25% eram de nível fácil, ou seja, existiam 5 perguntas de nível fácil e 15 de outros níveis.

Ele deseja que a quantidade de perguntas de nível fácil seja igual a 75% do total.

Considerando x a quantidade de perguntas fáceis, deveremos ter:

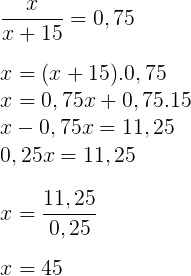
Resposta: E

Resolução

Observe que temos uma matriz 5×5, que relaciona o volume de transferências TED entre 5 bancos.

O elemento aij representa o volume de transferências transferidos do banco i para o banco j, ou seja, a soma dos elementos da linha 1 representa o volume transferido pelo banco 1, a soma dos elementos da linha 2 representa o volume transferido pelo banco 2, e assim sucessivamente.

Calculando o volume transferido por cada banco:

Banco 1: 2 + 0 + 2 + 2 = 6 milhões

Banco 2: 0 + 2 + 1 + 0 = 3 milhões

Banco 3: 1 + 2 + 1 + 1 = 5 milhões

Banco 4: 0 + 2 + 2 + 0 = 4 milhões

Banco 5: 3 + 0 + 1 + 1 = 5 milhões

Conclusão: O banco que transferiu o maior volume foi o banco 1.

Resposta: A

Resolução

O desconto deverá ser superior a 25% da parcela.

820 . 25% = R$ 205,00

A parcela a ser antecipada junto com a 30ª deverá ser inferior a:

820 – 205 = R$ 615,00

Utilizando a fórmula do enunciado, e sabendo que o nosso objetivo é calcular a quantidade de meses (n) após a 30ª parcela, de modo que o valor presente seja inferior a 615, temos a seguinte inequação:

P . (1+i)ⁿ > V

(1+i)ⁿ > V/P

Substituindo:

V = 820

P = 615

i = 1,32% = 0,0132

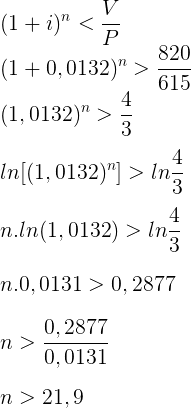
Veja que n deve ser superior a 21,9, ou seja, a parcela que deverá ser antecipada junto com a 30ª parcela é a parcela 52.

Resposta: C

Resolução

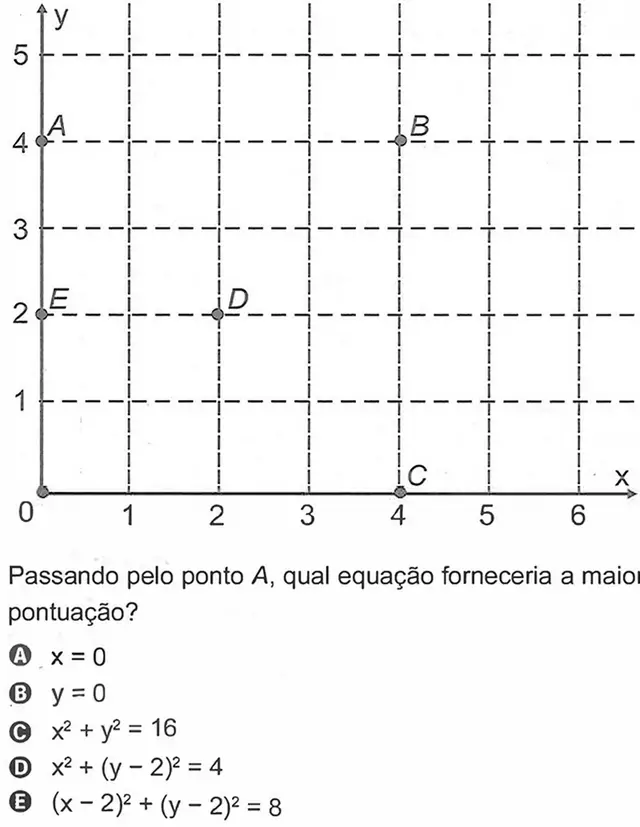
Pelas regras do jogo, a forma de se obter mais pontos é através de uma circunferência. Podemos desenhar uma infinidade delas passando pela origem e por um dos pontos A, B, C, D ou E, porém, como o objetivo é marcar mais pontos, deveremos passar pela maior quantidade possível.

Observe que a origem, forma com os pontos A, B e C um quadrado, que possui a propriedade de ser inscrito em uma circunferência. Neste caso, a equação da circunferência mencionada forneceria 6 pontos, que seria a maior quantidade possível.

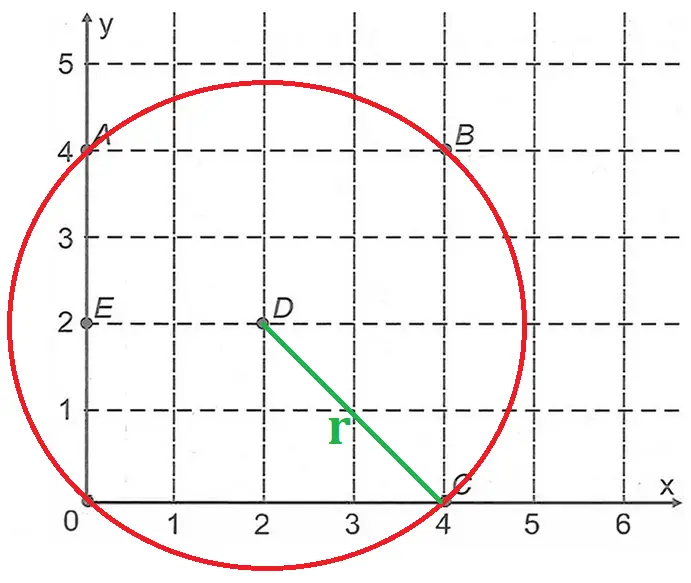
Analisando a equação geral da circunferência, precisamos de duas informações para determinarmos a equação da circunferência.

(x – x₀)² + (y – y₀)² = r²

As coordenadas do centro (2,2), e o raio, que pode ser calculado através do Teorema de Pitágoras, considerando que trata-se da diagonal de um quadrado de lado 2.

r² = 2² + 2²

r² = 4 + 4

r² = 8

Substituindo na equação geral:

(x – 2)² + (y – 2)² = 8

Resposta: E

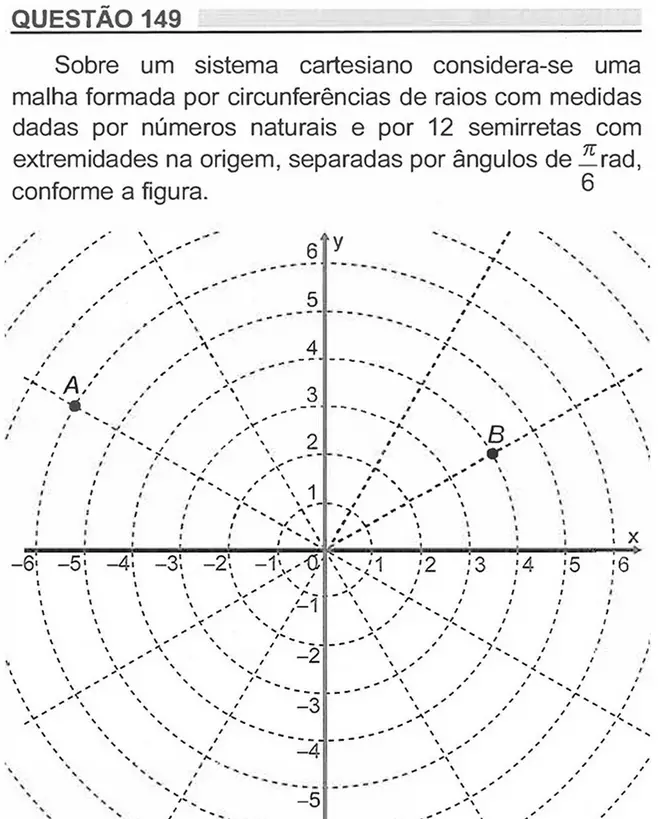
Resolução

Analisando a figura, podemos concluir que o percurso deverá ser feito no sentido anti-horário. Neste caso, passaríamos por 4 partes da circunferência, que foi dividida em 12, ou seja, independente do raio da circunferência, o percurso passará por 1/3 dela.

Sabendo que o comprimento de uma circunferência é dado por 2.π.r, o caminho a ser percorrido através da circunferência será dado por 2.π.r/3.

Acredito que a maioria dos alunos calculou a distância através do percurso que passa pela circunferência de raio 4. Neste caso teríamos:

2.π.r/3 + 2 = 2 . 3,1 . 4/3 + 2 = 10,3

Mas será que seria mais interessante passar por uma circunferência menor? Veja a distância quando utilizamos a circunferência de raio 1:

2.π.r/3 + 2 = 2 . 3,1 . 1/3 + 2 = 2 + 8 = 10

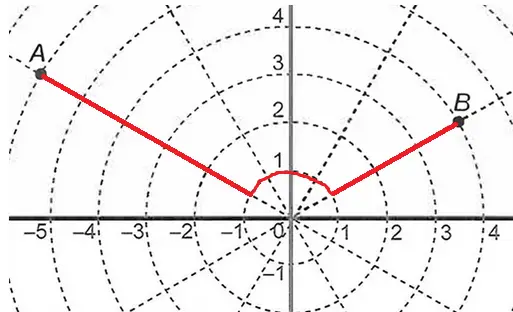
Neste caso, quando menor o raio da circunferência, menor será a distância total a ser percorrida. Esta informação poderia ser comprovada através das ferramentas de limites, que não são objeto de estudo neste momento.

Resposta: A

Resolução

Veja na figura abaixo o formato dos potes cilíndricos de 6 cm de altura e 4 cm de diâmetro.

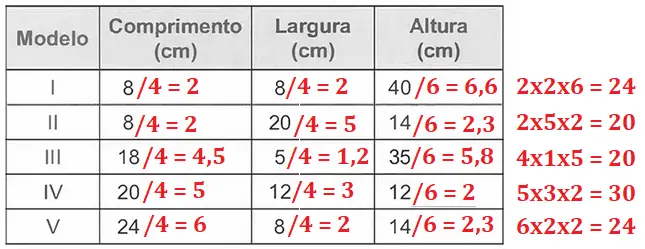
Dividiremos o comprimento e a largura de cada caixa por 4 (diâmetro do cilindro), e a altura por 6 (altura do cilindro). Com os resultados, poderemos calcular a quantidade de cilindros em cada caixa. Lembrando que nos interessa apenas a parte inteira do resultado, uma vez que não serão incluídos pedaços do cilindro.

Resposta: D

Resolução

Temos aqui uma progressão aritmética, da qual conhecemos o primeiro e o último termo e a razão.

80, 100, 120, …, 1380

a₁ = 80

r = 20

a_n = 1380

Utilizando a fórmula do termo geral de uma PA:

a_n = a₁ + (n – 1)r

1380 = 80 + (n – 1).20

1380 – 80 = 20n – 20

20n – 20 = 1300

20n = 1300 + 20

20n = 1320

n = 1320 / 20

n = 66

Como a prefeitura gastará, no máximo, R$ 8.000,00 por poste, o valor máximo a ser gasto será:

66 . 8000 = R$ 528.000,00

Resposta: C

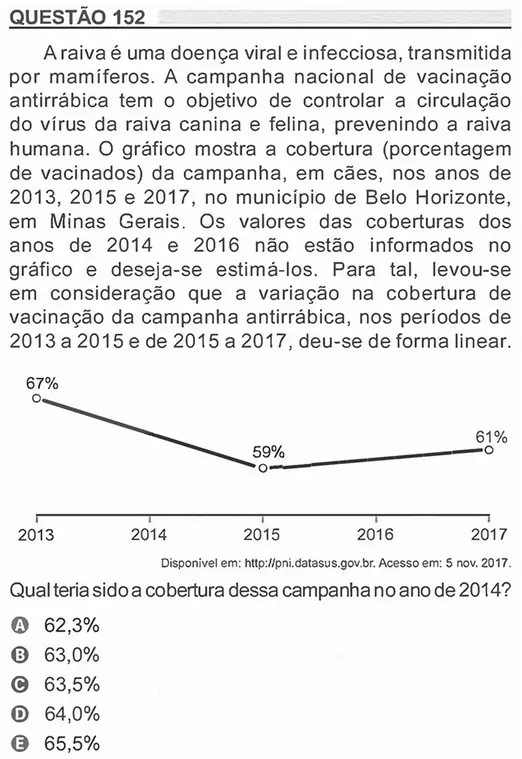
Resolução

Considerando que a variação na cobertura de vacinação da campanha antirrábica, no período de 2013 a 2015, deu se de forma linear, e sabendo que em 2013 a cobertura foi de 67%, e que em 2015 a cobertura foi de 59%, a cobertura referente ao ano de 2014 é a média aritmética das coberturas referentes a 2013 e 2015.

(67 + 59) / 2 = 126/2 = 63

Resposta: B

Resolução

O guindaste possui 15 metros de altura, e como a representação será dada em cm, também consideraremos a altura real em cm, ou seja, o guindaste possui 1500 cm.

Considerando o que a representação deve estar entre 0,5 cm e 1 cm, calcularemos as escalas para os dois valores:

• 0,5 / 1500 = 1/3000
• 1/1500

Como o enunciado informa “entre 0,5 cm e 1 cm”, descartamos os extremos, ou seja, x deve estar entre 1500 e 3000.

1500 < x < 3000

A esteira possui 90 metros (9000 cm) de comprimento, e a representação deve ser superior a 4 cm. Calculando a escala para 4 cm:

• 4 / 9000 = 1 / 2250

Como a representação deve ser superior a 4 cm, e quanto maior o tamanho do desenho, menor o denominador da escala, podemos concluir que x < 2250.

Considerando as duas equações:

1500 < x < 2250

Resposta: C

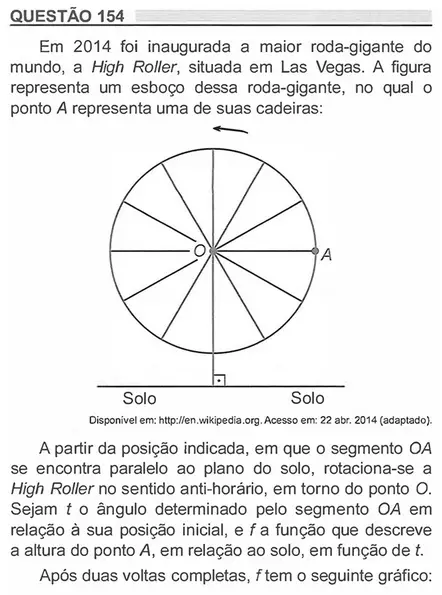
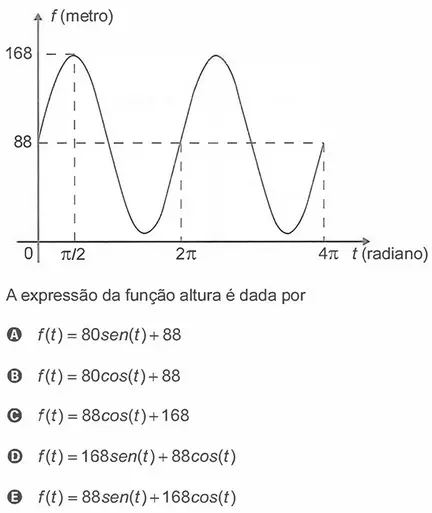
Resolução

Temos abaixo o gráfico da função seno.

f(t) = sen(t)

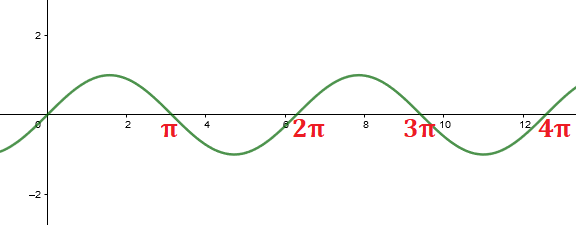
Quando multiplicamos a função seno por um número maior que 1, temos um aumento da imagem da função. Neste caso específico, multiplicando por 80, o domínio passa a ser o intervalo [-80, 80].

Veja como o gráfico é alterado:

f(t) = 80.sen(t)

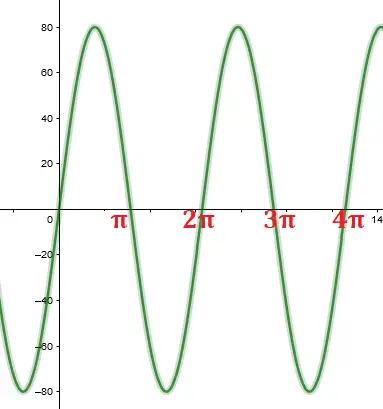
Quando somamos 88 a função acima, o domínio é alterado da seguinte forma:

[-80, 80] = [-80 + 88, 80 + 88] = [8, 168]

Veja como o gráfico é alterado:

f(t) = 80.sen(t) + 88

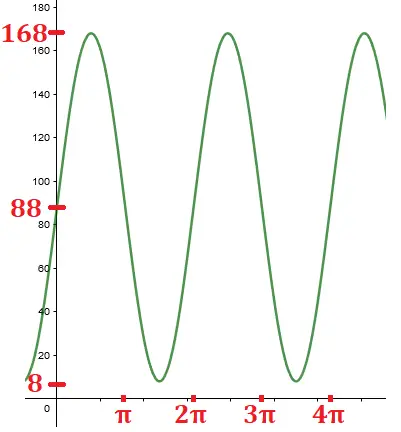
Resposta: A

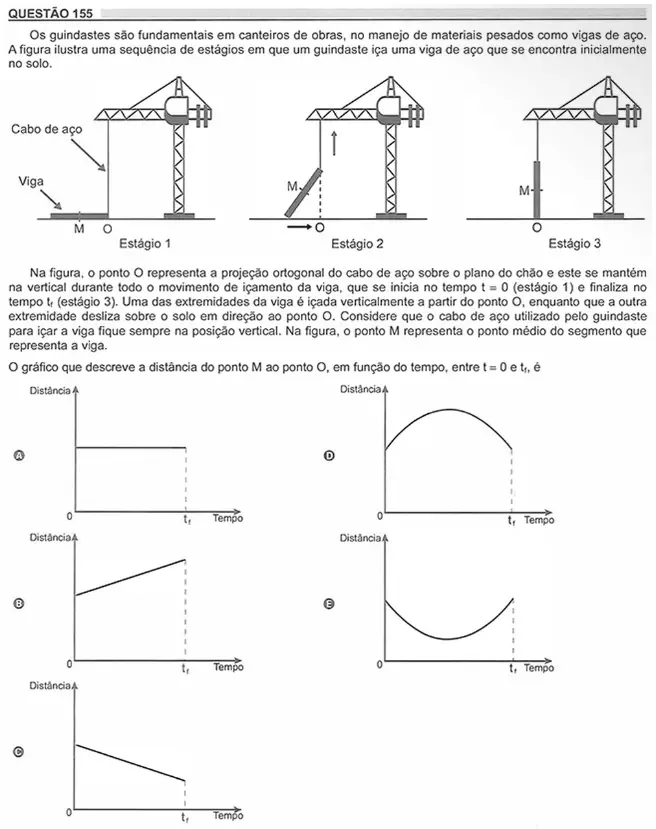
Resolução

Considere que o comprimento da viga é 2m, daí, a distância de M até O nos estágios 1 e 3 é igual a m.

Na figura abaixo, AB representa a viga, que foi içada formando um ângulo “a” qualquer com o solo.

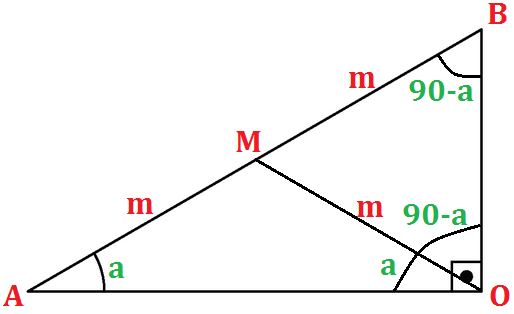
Veja na figura que os ângulos ABO e MOB são complementares de Â, ou seja, medem 90° – a.

Como o triângulo OMB possui dois ângulos iguais, trata-se de um triângulo isósceles, ou seja, OM = MB = m.

Perceba que escolhemos um ângulo “a” qualquer e concluímos que MO = m, ou seja, a distância entre O e M é sempre igual a m (constante).

Analisando as opções, o único gráfico que apresenta a distância constante é a letra A.

Resposta: A

Resolução

Analisaremos cada uma das opções, considerando que a pessoa deve retirar, sucessivamente e sem repetição, duas bolas pretas.

Opção 1.

A urna A possui 2 bolas pretas e um total de 6 bolas. Quando a pessoa retirar a primeira, a probabilidade de sair uma bola preta será de 2/6, e na segunda, a probabilidade será de 1/5.

(2/6) . (1/5) = 1/15 = 0,0666…

Opção 2.

A urna B possui 3 bolas pretas e um total de 10 bolas.

(3/10) . (2/9) = 1/15 = 0,0666…

Opção 3.

Deveremos passar, aleatoriamente, uma bola da urna C para a urna A.

A urna C possui 50% (1/2) de bolas pretas. Devemos analisar duas situações:

Se passarmos uma bola preta, passaremos a ter 3 bolas pretas de um total de 7 na urna A.

(1/2) . (3/7) . (2/6) = 1/14

Se passarmos uma bola de outra cor, passaremos a ter 2 bolas pretas de um total de 7 na urna A.

(1/2) . (2/7) . (1/6) = 1/42

Probabilidade total:

1/14 + 1/42 = (3 + 1)/42 = 4/42 = 2/21 = 0,095

Opção 4.

Deveremos passar, aleatoriamente, uma bola de D para C.

A urna D possui 50% de bolas pretas. Analisaremos as duas situações, assim como fizemos na opção 3.

Passando uma bola preta:

(1/2) . (3/5) . (2/4) = 3/20

Passando uma bola de outra cor:

(1/2) . (2/5) . (1/4) = 1/20

Probabilidade total:

3/20 + 1/20 = 4/20 = 1/5 = 0,2

Opção 5.

Resolução semelhante ao que fizemos nas opções 3 e 4.

1/2 . 4/7 . 3/6 = 1/7

1/2 . 3/7 . 2/6 = 1/14

Probabilidade total:

1/7 + 1/14 = (2 + 1)/14 = 3/14 = 0,21

Resposta: E

Resolução

Cada quadrado da Ecofont possui o seguinte formato:

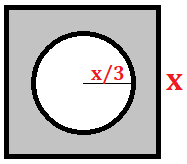
Veja que a área pintada é a diferença entre as áreas do quadrado e da circunferência:

A = x² – π.(x/3)²

A = x² – π.x²/9

A = x² . (1 – π/9)

Veja que a área pintada depende diretamente de x². Basta então observarmos que:

x/4 . x/4 = x²/16

Observe que quando reduzimos o lado do quadrado em 1/4, a área pintada é reduzida em 1/16, que é a redução pedida no enunciado.

Daí, a fonte deve ser reduzida em 1/4:

192/4 = 48

Resposta: B

Resolução

Veja na figura abaixo que a reta y=x divide o plano em duas regiões, uma onde y>x e outra onde y<x.

Também é possível perceber que os pontos estão sobre a reta, ou abaixo dela, ou seja, y≤x.

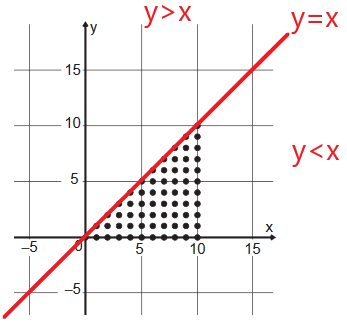
As outras duas limitações são mais simples:

Os pontos estão sobre, ou acima, da reta y=0.

Os pontos estão sobre, ou ao lado esquerdo da reta x=10.

Solução: 0 ≤ y ≤ x ≤ 10

Resposta: B

Em construção

Gostou da prova comentada do ENEM 2018 (matemática)?

Deixe o seu comentário.