Estudando matemática para concursos? Confira aqui tudo o que você precisa saber sobre os números complexos, onde falaremos sobre a definição, as operações e vários exemplos.
Não deixe de ver também as nossas publicações sobre os demais conjuntos numéricos.
Bom estudo!
Introdução
Os números complexos surgiram à medida que apareceram problemas envolvendo raiz quadrada de números negativos.
Isso era muito comum quando tentava-se resolver equações do segundo grau através da fórmula de Bhaskara.
Por exemplo, a equação do segundo grau x² + 2x + 5 = 0 tem Δ = -16.
Para resolver esse tipo de problema, foi definida a unidade imaginária i, onde i² = -1.
Definição
Chamamos de conjunto dos números complexos, representado pela letra C, o conjunto dos pares ordenados de números reais.
z ∈ C ⇔ z = (a,b), sendo que a,b ∈ R
Assim, um número complexo é um número z que pode ser escrito na forma algébrica da seguinte forma:
z = a + bi
Onde:
a e b são números reais
i é a unidade imaginária
Por definição, dizemos ainda que a é a parte real e b é a parte imaginária de z.
Exemplo:
O número z = 2 + 3i é um número complexo, onde:
a = 2 (parte real)
b = 3 (parte imaginária).
Relação com os Números Reais (R ⊂ C)
Como z = a + bi, e (a,b) é um par ordenado de números reais, podemos dizer que o conjunto dos números reais R está contido no conjunto dos números complexos C. Basta consideramos b = o. Veja:
5 = 5 + 0.i
3,4 = 3,4 + 0.i
√2 = √2 + 0.i
Operações com Números Complexos
Sejam z1 e z2 dois números complexos, onde:
z1 = a + bi
z2 = c + di.
Definiremos algumas operações entre z1 e z2.
- Igualdade de números complexos
Dois números complexos são iguais, se e somente se, possuem a mesma parte real e a mesma parte imaginária.
Dizemos que z1 = z2 ⇔ a = c e b = d.
Exemplos:
2 + 3i ≠ 2 + 4i
10 + i ≠ 9 + i
- Adição de números complexos
Definiremos a adição de dois números complexos z1 e z2 da seguinte forma:
z1 + z2 = a + bi + c + di
z1 + z2 = (a + c) + (b + d)i
Veja que basta somar as partes reais e as partes imaginárias.
Exemplo:
Somar os números complexos w = 5 + 6i e k = 2 + 4i.
w + k = (5 + 6i) + (2 + 4i)
w + k = (5 + 2) + (6 + 4)i
w + k = 7 + 10.i
- Subtração de números complexos
Definiremos a subtração de dois números complexos z1 e z2 da seguinte forma:
z1 – z2 = (a + bi) – (c + di)
z1 – z2 = (a – c) + (b – d)i
Veja que basta subtrair as partes reais e as partes imaginárias.
Exemplo:
Subtrair os números complexos w = 5 + 6i e k = 2 + 4i.
w – k = (5 + 6i) – (2 + 4i)
w – k = (5 – 2) + (6 – 4)i
w – k = 3 + 2i
- Multiplicação de números complexos
Definiremos o produto de dois números complexos z1 e z2 da seguinte forma:
z1 . z2 = (a + bi) . (c + di)
z1 . z2 = a.c + a.di + bi.c + bi.di
z1 . z2 = ac + ad.i + bc.i + bd.i²
z1 . z2 = ac + ad.i + bc.i + bd.(-1)
z1 . z2 = ac + ad.i + bc.i – bd
z1 . z2 = (ac – bd) + (ad + bc).i
Exemplo:
Multiplicar os números complexos w = 5 + 6i e k = 2 + 4i.
w.k = (5 + 6i) . (2 + 4i)
w.k = 5.2 + 5.4i + 6i.2 + 6i.4i
w.k = 10 + 20i + 12i + 24i²
w.k = 10 + 32i + 24.(-1)
w.k = 10 + 32i – 24
w.k = -14 + 32i
Potências de i
Já sabemos que i é a unidade imaginária em que está baseado todo o estudo dos números complexos. Vamos aprender a calcular o valor de in. Temos:
i0 = 1
i¹ = i
i² = -1
i³ = i².i = (-1).i = -i
i4 = i².i² = (-1).(-1) = 1
i5 = i4.i = 1.i = i
i6 = i5.i = i.i = -1
i7 = i6.i = -1.i = -i
É possível observar que as potências de i assumem uma sequência de apenas 4 resultados.
Sendo n um número Natural (n∈N), temos:
i4n = 1
i4n+1 = i
i4n+2 = -1
i4n+3 = -i
Exemplos:
i20 = 1, pois 20 = 4.5
i25 = i, pois 25 = 4.6 + 1
i10 = -1, pois 10 = 4.2 + 2
i15 = -i, pois 15 = 4.3 + 3
Plano de Argand-Gauss
O Plano de Argand-Gauss é o plano cartesiano utilizado para representar geometricamente os números complexos.
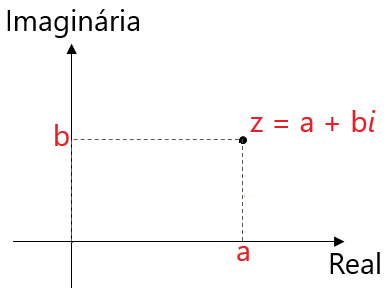
Módulo
O módulo de z = a + bi é representado por |z| e pode ser calculado da seguinte forma:
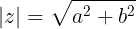
Observe que:
a = parte real
b = parte imaginária
Conjugado
O conjugado do número complexo por z = a + bi é dado por 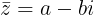 .
.
Exemplo:
z1 = 1 + 5i e 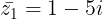
Gostou da nossa página sobre o conjunto dos números complexos?
Curta e compartilhe nas redes sociais.
