Estudando matemática para concursos? Confira aqui tudo o que você precisa saber sobre os monômios, onde falaremos sobre a definição, as operações e apresentaremos alguns exemplos.
Não deixe de ver também os nossos conteúdos sobre outros tópicos da álgebra.
Bom estudo!
DEFINIÇÃO
Um monômio, também chamado de termo algébrico, é uma expressão algébrica formada por um coeficiente numérico e uma parte literal. A grosso modo, trata-se do produto de um número por uma (s) incógnita (s). Desta forma, uma expressão não é monômio quando apresentar adição ou subtração ou quando possuir incógnita no denominador.
Exemplos de expressões que são monômios
- 2x
Coeficiente numérico: 2
Parte literal: x
- 10xy²z³
Coeficiente numérico: 10
Parte literal: xy²z³
- kw
Coeficiente numérico: 1
Parte literal: kw
Exemplo de expressões que não são monômios
- x + 2y²
- 5 + x
- x/y
- x-5
- k + w + z
SEMELHANÇA DE MONÔMIOS
Como vimos, um monômio é dividido em coeficiente numérico e parte literal. Dizemos que dois monômios são semelhantes quando as partes literais são iguais. Veja:
- Os monômios 2x³y³ e 5x³y³ são semelhantes
- Os monômios 10xy³ e 10xy² não são semelhantes
ADIÇÃO E SUBTRAÇÃO DE MONÔMIOS
Dois monômios podem ser somados ou subtraídos apenas quando são semelhantes, ou seja, quando as partes literais são exatamente iguais. Neste caso, repetimos a parte literal e somamos os coeficientes numéricos. Veja:
- 2x³y³ + 5x³y³ = 7x³y³
- 2x³y³ – 5x³y³ = -3x³y³
- 2x² + 5x² = 7x²
MULTIPLICAÇÃO DE MONÔMIOS
Multiplicamos os coeficientes e as partes literais.
É muito importante que lembremos de uma das propriedades da potenciação:
an.am = an+m
Exemplos:
- 3xy . 4kx² = 12x³ky
- 2xyz . 10x²y²z² = 20x³y³z³
- 2xyz . 3kw = 6xyzkw
DIVISÃO DE MONÔMIOS
Dividimos os coeficientes e as partes literais.
Vale recordar mais uma propriedade da potenciação:
am : an = am-n
Exemplos:
![]()
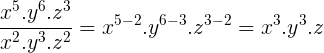
POTENCIAÇÃO DE MONÔMIOS
Para efetuarmos a potenciação, basta relembrarmos as seguintes propriedades:
amn = am.n
(a.b)n = an.bn
Exemplos:
- (3x³)² = 3².x3.2 = 9.x6
- (4xyz)³ = 4³.x³.y³.z³ = 64x³y³z³
Gostou da nossa página especial sobre monômios?
Curta e compartilhe nas redes sociais.
