Você sabe o que são intervalos reais? Veremos aqui a definição, operações e aplicações para você gabaritar concursos e ENEM.
Bom estudo!
Definição
O conjunto dos números reais, representado pela letra R, possui vários subconjuntos. Alguns desses subconjuntos são chamados de intervalos reais, e são determinados por meio de desigualdades.
Imagine, por exemplo, a infinidade de números reais existentes entre os números 1 e 2. Podemos dizer que todos os números Reais entre 1 e 2 formam um subconjunto dos números reais.
Podemos representar o os números reais que estão no intervalo real entre 1 e 2 de três formas diferentes:
- Utilizando colchetes
I = ]1, 2[
- Utilizando desigualdades
I = {x∈R | 1<x<2}
- Utilizando a reta real

Perceba que representamos o intervalo entre 1 e 2, porém sem incluir esses dois extremos. Neste caso, dizemos que o intervalo é aberto nos extremos 1 e 2.
Veja agora como é a representação deste intervalo, porém com a inclusão dos números 1 e 2 (neste caso, dizemos que o intervalo é fechado nos dois extremos):
- Utilizando os colchetes
I = [1, 2]
Utilizando as desigualdades
I = {x∈R | 1≤x≤2}
Utilizando a reta real

Observou a diferença?
Quando utilizamos os colchetes, nós mudamos o sentido, quando utilizamos as desigualdades, nós alteramos para “menor ou igual”, e quando utilizamos a reta real nós a pintamos. Simples não é mesmo?
Obs: Alguns autores utilizam parênteses no lugar dos colchetes quando pretendem representar intervalos abertos. Veja:
[1, 2[ = [1, 2)
]1, 2[ = (1, 2)
Vamos a outro exemplo:
Representar o subconjunto dos Reais maiores ou iguais a 1:
Utilizando os colchetes:
I = [1, ∞[
Utilizando as desigualdades
I = {x∈R | x≥1}
Utilizando a reta real:

Operações com intervalos reais
A utilização da reta real na resolução de operações entre conjuntos formados por intervalos reais é muito importante. Através dela é possível observar com mais facilidade as operações de união, interseção e diferença entre conjuntos. Veja o exemplo:
Considere os conjuntos abaixo:
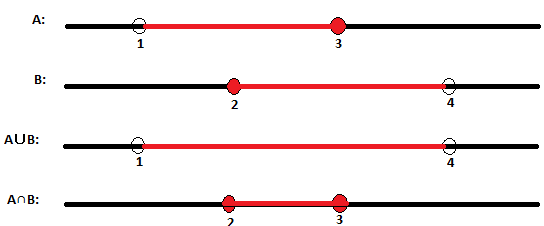
A = ]1, 3]
B = [2, 4[
Utilizaremos a reta real para representaremos os intervalos formados pela união e pela interseção de A e B.
Lembrando que:
- A união de dois conjuntos A e B é formada por todos os elementos que pertencem a A ou que pertencem a B.
- A interseção de dois conjuntos A e B é formada por todos os elementos que pertencem a A e também pertencem a B.
Temos:
A∪B = ]1, 4[
A∩B = [2, 3]
Diferença entre intervalos reais
A diferença entre conjuntos é a operação que mais gera dúvidas por parte dos alunos.
Basta lembrar que “A – B” é o conjunto formado pelos elementos que pertencem ao conjunto A, porém NÃO pertencem ao conjunto B.
Considerando o exemplo anterior, com A = ]1, 3] e B = [2, 4[, temos:
Elementos que pertencem a A e não pertencem a B:
A – B = ]1, 2[
Elementos que pertencem a B e não pertencem a A:
B – A = ]3, 4[
Veja também no YouTube.
Gostou da nossa publicação sobre os intervalos reais?
Deixe o seu comentário.
eu nao estou conseguindo entender?
Qual é a sua dúvida Fernanda?
Tem que ter prontidão do assunto de conjuntos para entender o que é U e ∩. E saber que as bolinhas fechadas elas inclue o valor ou quando vim no conjunto assim [1,5] inclui q os dois são fechado ou quando vim na expressão assim {x E R/ 3 ≥ x ≥ 2} esse maior ou igual significa bolinha fechada, o e so maior ou so menor bolinha aberta pois a aberta ela exclui o valor dado na expressão e pode vim com o colchete invertido tipo ][ que diz que será bolinha aberta.
Professor Jordon com todo respeito primeiro agradeço pelo artigo publicado, em segundo queria que o Senhor me desse mais esclarecimentos em relação as aulas sobre conjuntos, agradecia o favor professor!
Olá Eugênio,
Qual é a sua dúvida?
perfect , muito bom
Alias de ser bem iniciante
perfect , muito bom
Apesar de ser bem simples e de fácil entendimento
Olá professor, parabéns pelo artigo, eu estou tendo dificuldades na hora de representar com os colchete aberto ou fechado.
Olá Angel!
Seguem dois exemplos para facilitar a compreensão:
Conjunto dos números reais entre 0 e 1, incluindo os extremos:
[0,1]
Conjunto dos números reais entre 0 e 1, excluindo os extremos:
]0,1[
Exemplo: considere os intervalos
M = [ 1,5 ] e K = [ 3,7 ]
Determine:
União [ 1,7 [
Intersecção [ 3,5]
M – K = [ 1,3 [ eu não entendi porque o colchete está aberto [
K – M = ] 5,7[ não entendi porq o 5 está aberto ]
Angel,
Temos que fazer uma pequena correção:
M U K = [1,7]
Em relação as dúvidas:
M-K é o conjunto dos elementos que estão em M, mas não estão em K. O colchete está aberto pois 3 pertence a K.
Para K-M o raciocínio é o mesmo.
Espero ter ajudado.
Muito boa explicação,me ajudou muito.
Excelente explicação do nobre , competente e eloquente professor , vai ajudar muito aqueles que querem prestar concursos.
entao como eu posso resolver essa questao ?
A=(-4;5) e B=[-6;3)
a) A U B
b) A U B
c) A – B
d) B – A
a) A U B = [-6, 5)
b) A ∩ B = (-4, 3)
c) A – B = [3, 5)
d) B – A = [-6, -4]
Professor, A – B não seria (4,5)?
Luciano,
observe que o intervalo [3,5) está em A, porém não está em B.
Eu queria tirar uma duvida nessa questão: Dados dos intervalos A= [2,8] e B= [7,20]; determine A^c em que o universo é o conjunto R. ?
Conjunto dos números reais maiores que – 4 em intervalo
Seja R o conjunto universo e considere os conjuntos :
A=]-10;0] ;
B=[2;5[ ;
C=]-2;5] ;
D=[3;10[
a)A interseccao com C ;
b)B reuniao com C e interseccao com D ;
c)B interseccao com C ;
d)A reuniao com B e interseccao com C ;
e)A interseccao com D.
Por favor me ajudem humildemente peco !