Veja aqui um método simples e rápido de encontrar as coordenadas do ponto de interseção de duas retas.
Não deixe de ler também nossos outros conteúdos sobre a geometria analítica.
Bom estudo!
Quando duas retas estão dispostas no mesmo plano, existem três posições relativas entre elas: podem ser coincidentes, paralelas ou concorrentes.
Retas coincidentes – possuem todos os pontos em comum.
Retas paralelas – não possuem nenhum ponto em comum.
Retas coincidentes – possuem apenas um ponto em comum.
Vejamos agora como determinar as coordenadas do ponto de interseção de duas retas concorrentes, e como identificar quando duas retas são coincidentes ou paralelas.
Sejam r e s duas retas dispostas no mesmo plano. Podemos determinar as coordenadas do ponto P de interseção das duas retas resolvendo o sistema formado pelas equações das mesmas. Veja:
Sendo a1.x + b1.y + c1 = 0 a equação geral da reta r, e a2.x + b2.y + c2 = 0 a equação geral da reta s, o ponto de interseção das duas retas pode ser determinado resolvendo o sistema de equações abaixo:
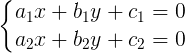
Para facilitar a resolução do sistema de equações, sugerimos que o aluno faça a transformação da equação geral para a equação reduzida da reta. Este procedimento será adotado na resolução dos exemplos e também facilitará a identificação de retas paralelas.
Exemplo 1. Determinar o ponto de interseção das retas r e s, cujas equações gerais são, respectivamente, 2x + y – 1 = 0 e x – y + 2 = 0.
Transformando as equações gerais em reduzidas:
- Reta r
2x + y – 1 = 0
y = -2x + 1
- Reta s
x – y + 2 = 0
y = x + 2
O próximo passo é resolver o sistema abaixo:
y = -2x + 1
y = x + 2
Subtraindo a primeira da segunda equação:
y – y = x + 2 – (-2x + 1)
0 = x + 2 + 2x – 1
3x + 1 = 0
3x = -1
x = -1/3
Substituindo o valor de x na segunda equação:
y = x + 2
y = -1/3 + 2
y = 5/3
O ponto de interseção das retas é o ponto (-1/3, 5/3).
Exemplo 2. Determinar o ponto de interseção das retas r e s cujas equações são, respectivamente, x – y + 2 = 0 e 3x + y – 5 = 0.
Transformando as equações na forma reduzida:
- Reta r
x – y + 2 = 0
y = x + 2
- Reta s
3x + y – 5 = 0
y = -3x + 5
Devemos resolver o sistema:
y = x + 2
y = -3x + 5
Subtraindo a segunda da primeira equação:
y – y = x + 2 – (-3x + 5)
0 = x + 2 + 3x – 5
0 = 4x – 3
4x = 3
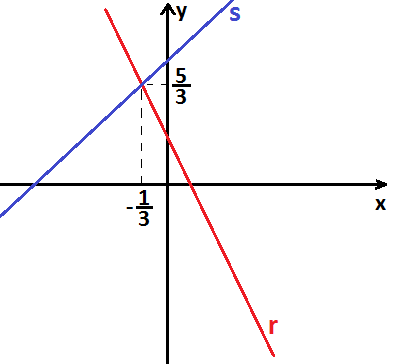
x = 3/4
Substituindo o valor de x na primeira equação:
y = x + 2
y = 3/4 + 2
y = 11/4
O ponto de interseção das retas é o ponto (3/4, 11/4).
Exemplo 3. Determine o ponto de interseção das retas r e s, cujas equações são, respectivamente, x + y + 1 = 0 e 2x + 2y + 4 = 0.
Transformando as equações na forma reduzida:
- Reta r
x + y + 1 = 0
y = -x – 1
- Reta s
2x + 2y + 4 = 0
2y = -2x – 4
y = -x – 2
Se tentarmos resolver o sistema de equações, veremos que trata-se de um sistema impossível. Isso porque temos duas equações distintas, porém com o mesmo coeficiente angular. Sempre que isto ocorrer teremos duas retas com a mesma inclinação, porém localizadas em locais diferentes do plano cartesiano, ou seja, as retas serão paralelas e não haverá ponto em comum.
Exemplo 4. Determine o ponto de interseção das retas r e s, cujas equações são, respectivamente, x – y + 5 = 0 e 2x – 2y + 10 = 0.
Transformando as equações na forma reduzida:
- Reta r
x – y + 5 = 0
y = x + 5
- Reta s
2x – 2y + 10 = 0
2y = 2x + 10
y = (2x + 10) / 2
y = x + 5
Veja que as retas possuem a mesma equação reduzida. Neste caso as retas são coincidentes, ou seja, possuem todos os pontos em comum.
Gostou do nosso conteúdo sobre a interseção de retas?
Curta e compartilhe nas redes sociais.
