Estudando matemática para concursos? Confira mais um post sobre geometria analítica, onde vamos estudar a definição, a equação e exemplos de hipérbole.

Não deixe de ver também nossas publicações sobre os outros tópicos da geometria analítica.

Bom estudo!

 

 

DEFINIÇÃO

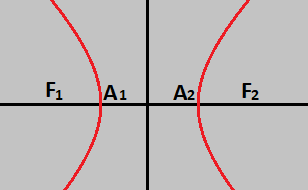
Chamamos de hipérbole a figura formada pelos pontos do plano, onde o módulo da diferença da distância a dois pontos fixos (focos F₁ e F₂) é sempre uma constante 2a:

|d(P, F₁) – d(P, F₂)| = 2a.

Veja:

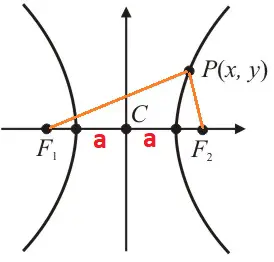
Figura 1

 

 

ELEMENTOS DA HIPÉRBOLE

F₁ e F₂ são os focos

2c é a distância entre os focos

C é o centro

2a é o eixo real ou transverso (distância entre A₁ e A₂)

2b é o eixo imaginário (distância entre B₁ e B₂)

c/a é a excentricidade

Vejamos nos gráficos abaixo como os elementos da hipérbole estão posicionados.

 

Gráfico da hipérbole com focos sobre o eixo x.

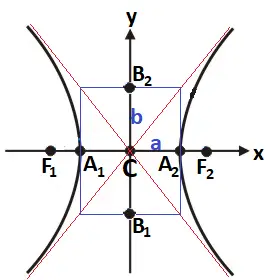
Figura 2

Gráfico da hipérbole com focos sobre o eixo y.

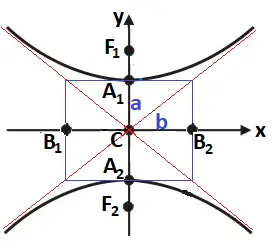
Figura 3

 

RELAÇÃO ENTRE OS VALORES a b c

Em toda hipérbole vale a seguinte relação:

c² = b² + a²

A relação é muito útil quando sabemos dois valores e queremos achar o terceiro. Por exemplo, sabemos o tamanho dos dois eixos e queremos saber a distância focal.

 

 

EQUAÇÃO DA HIPÉRBOLE COM CENTRO EM (0,0)

Como vimos, uma hipérbole com centro C(0,0) pode ter os focos no eixo x ou no eixo y.

 

1) Focos sobre o eixo x.

É o caso da hipérbole apresentada na figura 2.

A equação reduzida será:

2) Focos sobre o eixo y.

É o caso da hipérbole apresentada na figura 3. A equação reduzida será:

 

EQUAÇÃO DA HIPÉRBOLE DE CENTRO (x₀, y₀)

Você deve ter reparado que mencionamos apenas os casos de hipérboles de centro na origem. Não é uma regra, o centro pode estar em qualquer ponto do plano cartesiano.

Na figura abaixo temos um exemplo de hipérbole cujo centro não se encontra na origem.

 

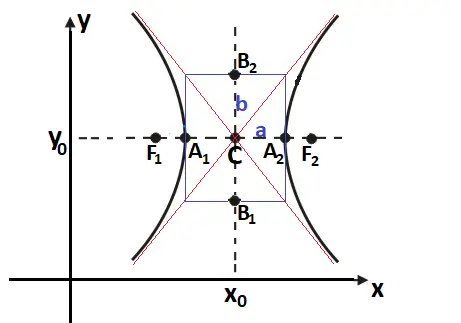
Neste caso, a equação das hipérboles de centro C(x₀, y₀) apresentam uma pequena mudança. Veja:

 

Hipérbole de abertura leste-oeste

 

Hipérbole de abertura norte-sul

 

EXEMPLO

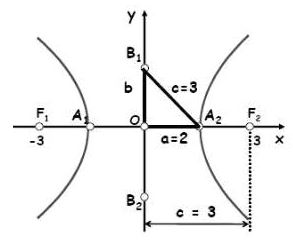
Determinar os elementos e a equação da hipérbole de focos (-3, 0) e (3, 0), sabendo que a menor distância entre os dois ramos da hipérbole é 4.

Nessas condições, veja como fica nossa hipérbole:

O valor a = 2 foi retirado da informação que a menor distância entre os ramos é 4.

O valor c = 3 foi retirado das coordenadas dos focos, de onde sabemos que a distância entre eles é 6.

O centro tem como coordenadas (0, 0).

 

Calculando o valor de b:

b² = c² – a²

b² = 3² – 2²

b² = 9 – 4

b² = 5

b = √5

 

Equação da hipérbole:

 

Gostou da nossa página sobre hipérbole?

Deixe o seu comentário.