Nesta página vamos falar sobre a função inversa, abordando a definição e apresentando alguns exemplos.
Pede-se que o aluno tenha um conhecimento prévio sobre a definição e dos tipos de funções, em especial a função bijetora.
Bom estudo!
Definição
Em nossa página sobre os tipos de funções, apresentamos como exemplo a função f:A→B, com A = {0, 1, 2} em B = {1, 3, 5}, definida pela lei f(x) = 2x + 1.
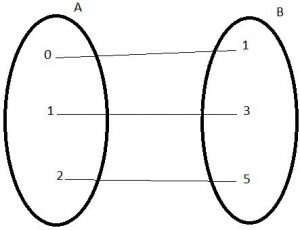
Analisando o diagrama, claramente f é bijetora pois é injetora e sobrejetora ao mesmo tempo.
Sempre que uma função for bijetora, existe uma função que faz exatamente o contrário da função original, levando os elementos do conjunto B aos elementos do conjunto A, e a esta função damos o nome de função inversa.
Representação
Seja a função f abaixo:
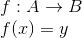
A inversa da função f é representada da seguinte forma:
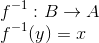
Exemplo 1:
Voltando ao exemplo acima, vamos construir a inversa da função f. Vejamos como fica o seu diagrama:
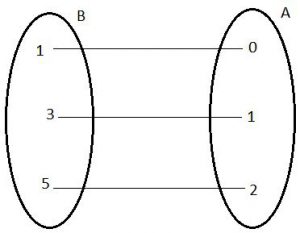
Como podemos perceber, a inversa de f leva cada um dos elementos do conjunto B a um elemento do conjunto A, exatamente o contrário do que f fazia.
Mas como a função inversa faz isso? Com certeza não pode ser através da regra utilizada por f.
Na função f tínhamos y em função de x:
y = 2x + 1
A regra da função inversa pode ser descoberta colocando x em função de f. Temos:
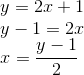
Agora que já descobrimos a regra da função inversa de f, podemos representá-la:
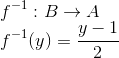
Exemplo 2:
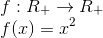
Observe que restringimos o domínio e o contradomínio aos números reais não negativos, de modo a termos uma função bijetora, e consequentemente inversível.
Vamos determinar a regra da inversa:
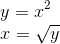
Veja como fica a representação da função inversa:
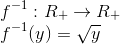
Observação
Assim que você se sentir seguro sobre a função inversa, sugiro que volte a representar a variável pela letra x, pois facilitará o seu entendimento, principalmente quando precisar desenhar o gráfico de f-¹.
Veja:
Exemplo 1:
f-¹(x) = (x-1)/2
Exemplo 2:
f-¹(x) = √x
O mais importante é não ficarmos presos a letra que utilizamos, pois temos o costume de utilizar algumas letras na matemática, mas poderiam ser quaisquer outras.
Aprendeu a identificar a função inversa?
Deixe o seu comentário.
