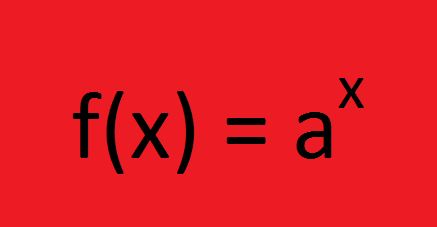Nesta página veremos o significado da expressão “crescimento exponencial”, que é analisado através de uma função exponencial. Aprenderemos a definição, o formato do gráfico e analisaremos alguns exemplos. Como o próprio nome já diz, é importantíssimo que o aluno tenha domínio dos conteúdos de função e de potenciação.
Vamos ao que interessa…
Definição
Definimos como função exponencial toda função f de R em R, dada por uma lei no formato abaixo, onde “a” é um número real maior que 0 (zero) e diferente de 1.
Exemplos:
Gráfico
Construiremos o gráfico de duas funções exponenciais para analisarmos como elas se comportam.
O primeiro exemplo de função exponencial possui a>1 e o segundo possui a<1.
Exemplo 1.
Temos que:
Veja como fica o gráfico quando ligamos alguns desses pontos:
Exemplo 2.
Temos que:
Veja como fica o gráfico quando ligamos alguns desses pontos:
Notou a diferença? Veremos agora como o valor de “a” é determinante para o formato do gráfico.
Propriedades da função exponencial
A função exponencial possui várias propriedades interessantes e muito úteis na resolução de exercícios:
Propriedade 1: O gráfico sempre passará pelo ponto (0, 1).
A propriedade é bem simples de se verificar. Pela construção da função exponencial, toda vez que tivermos x=0, teremos y=1. Isso porque “todo número elevado a zero é igual a 1”.
Propriedade 2: Se a>1, então a função exponencial será crescente.
Veja o gráfico do exemplo 1.
Propriedade 3: Se 0<a<1, então a função exponencial será decrescente.
Veja o gráfico do exemplo 2.
Propriedade 4: Para todo a>0 e todo x∈R, a função f é positiva.
Podemos concluir que o gráfico de f sempre estará acima do eixo x.
Aprendeu a identificar uma função exponencial?
Deixe seu comentário e compartilhe nas redes sociais.