Você sabe o que é uma função composta? Veremos aqui a definição e vários exemplos para você arrebentar nas questões de matemática das provas de concursos e ENEM.
Bom estudo!
Definição de função
Uma função é uma relação entre dois conjuntos A e B quaisquer, que associa cada elemento de A a um único elemento de B.
É muito comum utilizarmos a letra f para representarmos uma função:
f : A → B
Lê-se: f de A em B
Os conjuntos A e B recebem nomes especiais:
- A é o Domínio da função;
- B é o Contradomínio da função.
Exemplo 1:
f : A → B
f(x) = 5x
A = {1, 2, 3}
B = {5, 10, 15}
Definição de função composta
Função composta é uma combinação de duas ou mais funções.
Sejam as funções f: A → B e g: B → C.
A função h: A → C, tal que h(x) = g(f(x)) é chamada de função composta, sendo representada por h(x) = gof(x)
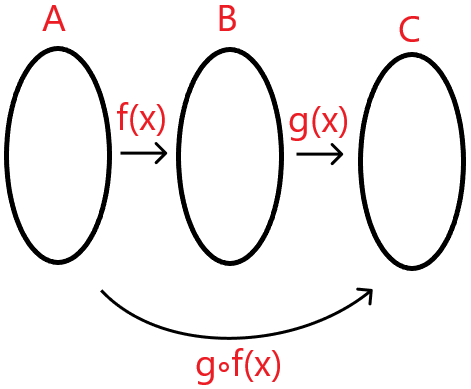
Exemplo 2: Determinar a função composta gof(x), sabendo que:
- f : A → B, com f(x) = 5x
- g : B → C, com g(x) = 10x
Temos:
gof(x) = g(f(x)) = g(5x) = 10.(5x) = 50x
Exemplo 3: Determinar a função composta gof(x), sabendo que:
- f : A → B, com f(x) = x²
- g : B → C, com g(x) = 3x + 1
Temos:
gof(x) = g(f(x)) = g(x²) = 3.(x²) + 1 = 3x² + 1
Exemplo 3: Determinar a função composta fog(x), sabendo que:
- f : A → B, com f(x) = x²
- g : B → C, com g(x) = 3x + 1
Temos:
fog(x) = f(g(x)) = f(3x + 1) = (3x + 1)² = 9x² + 6x + 1
Aprendeu a calcular a função composta?
Deixe o seu comentário.
