Confira aqui vários exercícios resolvidos sobre o fatorial de um número natural, ferramenta muito utilizada na análise combinatória.
Sugerimos que acesse primeiramente o nosso conteúdo sobre o assunto, onde você vai encontrar a definição de fatorial e vários exemplos.
Bom estudo!
Questão 1. Calcule o valor das frações abaixo:
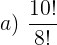
Resolução
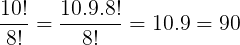
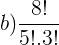
Resolução
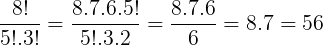
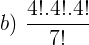
Resolução
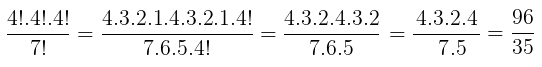
Questão 2. Simplifique as expressões abaixo:
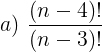
Resolução
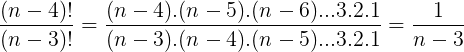
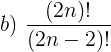
Resolução
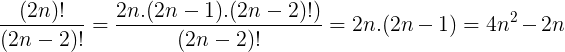
Questão 3 (ESFCEX 2006). Para n natural, n≥2, quanto vale a expressão abaixo?
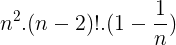
a) n!
b) (n − 1)!
c) (n + 1)!
d) n.(n + 1)!
e) (n − 2)!
Resolução
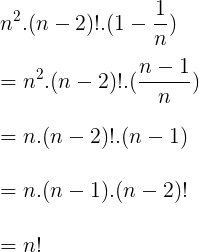
Resposta: A
Gostou das nossas questões comentadas sobre fatorial?
Deixe o seu comentário.

eu gostaria de tirar uma dúvida, em (n-4)!/(n-3)! o menor fatorial não seria o (n-4) sendo assim tendo que abri-lo? no caso o resultado ficaria n-3, Obrigada!
Olá Jessica!
(n-4)! = (n-4).(n-5).(n-6)….3.2.1
(n-3)! = (n-3).(n-4).(n-5).(n-6)….3.2.1
(n-4)!/(n-3)! = 1/(n-3)
O resultado é 1/(n-3)
poderia me ajudar a simplificar esta expressao?
n! + (n + 1)! / n!+ 2(n-1)!
Olá Willian!
Não há muita coisa para simplificar.
Favor verificar se não existe algum erro de digitação.
n! + (n + 1)!/n! + 2(n-1)!
n! + (n + 1) + 2(n-1)!
n(n-1)! + (n + 1) + 2(n-1)!
(n+2).(n-1)! + (n+1)
n (n – 1) ! + (n + 1) n (n – 1) ! / n(n -1) ! + 2(n – 1) ! passa a régua em ( n – 1) !
n + (n + 1) n / n + 2 —> coloca n em evidência no numerador —> n (1 + (n + 1)) / n + 2) —>
n ( n + 2) / (n + 2) —> passa a régua em (n + 2) —-> Resposta: n
eu gostaria de tirar uma duvida como fazer (n+3)! . (n-1)! dividido por
(n-2)! . (n+2)!
Olá Paulo!
Basta fazer as seguintes substituições:
(n+3)! = (n+3).(n+2)!
(n-1)! = (n-1).(n-2)!
NA QUESTAO B SOBRE FATORIAL
DE ONDE VEIO O 2 ?
Gustavo,
3! = 3.2.1 = 3.2
calcule (n+1)!=4!
Gostaria de entender a questão 3 a partir do momento em que fica
n.(n-1)(n-2)
Olá Julia!
Temos n.(n-1).(n-2)!
Como (n-2)! = (n-2).(n-3)…3.2.1, temos que:
n.(n-1).(n-2)! = n.(n-1).(n-2).(n-3)…3.2.1 = n!
Excelente Blog, tem me ajudado muito.
Olá! Essa última questão da ESFCEX eu nbão entendi bem… Não sei como efetuar o9 (1-1/n)
Olá Juliana!
Você deve calcular o mmc e efetuar a subtração.
Olá ,na questão da Esfcex ,eu não entendi por que o n²! saiu ,poderia me explicar
Olá Monica!
Temos n.(n-1).(n-2)!
Como (n-2)! = (n-2).(n-3)…3.2.1, temos que:
n.(n-1).(n-2)! = n.(n-1).(n-2).(n-3)…3.2.1 = n!
peço pra mi explicar isso (n+3)! -2 (n+3)!÷(n+2)! -n!
Olá Leyda!
Favor revisar a expressão.
Pode ajudar a simplificar 7!-8!+6!
8!-6
Olá Salmina!
Basta colocar o 6! em evidência.
desculpem mas como posso resolver um caso destes:
-(n-2)!(n+3)!
Fulgêncio!
Favor confirmar a expressão que você escreveu.
Como eu cálculo o valor de n na seguinte expressão: (n+2)!=6n!
Olá Isabela!
A igualdade proposta valerá apenas quando n+2 = 6n
6n = n+2
6n – n = 2
5n = 2
n = 2/5
Como n é um número natural, o seu problema não possui solução.
Ola Jordon! Esse exercício é diferente da Isabela pelo que o resultado também é diferente.
Olá!
O exercício original é como?
Ola Jordon e Isabela!
Nao seria: (n+2).(n+1).n!=6n! -> (n+2).(n+1) = 6 -> n^2+3n+2 = 6 -> n^2+3n – 4 =0 -> n = 1 ou n = -4, donde, como n é não negativo, n =1 (?)
Rogério,
O comentário anterior não deixou claro se temos (6n)! ou 6.(n!). Considerando a segunda opção, você está correto.
(n+3)! (n+1)! / n!(n+1)
(n+3)! (n+1)! / n!(n+1)
(n+3)!.(n+1).n! / (n+1).n!
(n+3)!
12! / 10! + 9!
Olá Tayllane!
12! / 10! + 9!
12.11.10! / 10! + 9!
12.11 + 9!
132 + 9!
2= / m!/1/4 – 7 / 1 / ( m+1)!/
Por favor explique-me como resolver n! + (n-1)! / (n+1)! – n! = 6/25
Olá Rafaela,
n! + (n-1)! / (n+1)! – n! = 6/25
(n-1)! / (n+1).n.(n-1)! = 6/25
1/(n+1).n = 6/25
1/(n²+n) = 6/25
6.(n²+n) = 25
…
Olá! como ficaria :
3n!/(n+2)! poderia me ajudar
3n!/(n+2)! = 3n!/(n+2)(n+1).n! = 3/(n+2)(n+1)
Olá como Ficaria (n-8)!(n-9)=12
Olá Jaislane!
12 = 3.2.1.2 = 3!.2 = (11-8)!.(11-9)
Daí, n = 11.
Por favor, me auxiliem com esta questão. Disseram que é fatorial.
Uma seleção de 6 meninos e 4 meninas, deve ser escolhida dentre 10 meninos e 7 meninas para realização de um comercial de TV. De quantos modos diferentes esse comercial pode ser realizado? sabendo que todos terão funções idênticas?
Gostaria de saber a resolução da seguinte questão : (n+1)!+n!/2n!. Obrigada.
Olá Ana!
(n+1)! + n!/2n!
(n+1)! + 1/2
Sugiro que confira a expressão.
como resolver 12!/ (3!)^4 ?
Olá Juçara!
12!/ (3!)^4
12!/ 3!.3!.3!.3!
12.11.10.9.8.7.6.5.4.3.2.1/3.2.3.2.3.2.3.2
A simplificação fica por sua conta…
Jordon, preciso saber… Como seria se a expressão fosse (n – 9)! = 1? E (n – 2)! = 2(n – 4)? Por favor, me ajdaaa
Olá Beatriz!
(n – 9)! = 1
(n – 9) = 1
n = 1 + 9
n = 10
(n – 9)! = 0
(n – 9) = 0
n = 9
(n – 2)! = 2(n – 4)
(n-2).(n-3).(n-4).(n-5)! = 2.(n-4)
(n-2).(n-3).(n-5)! = 2
Veja que não tem solução para n = 1, 2, 3, 4, 5, 6…
Olá tem esse arquivo em pdf?
Olá Asaf!
Apenas no site…
Olá! Como eu calculo (n-5)! / (n-3) =1/28
Não consigo achar o valor dessa expressão: 37! – 36!/35!
Oi,
Porque quando a divide 10!/8!, sempre começa do 10 e não do 8??
Anna,
Porque 10! = 10.9.8.7.6.5.4.3.2.1
n!/(n-2)!+(n-1)
Qual é o valor de n na seguinte situação: n!/n+1=(n+1)!
Vanessa,
Você deve observar que (n+1)! = (n+1).n!
Simplificar a expressão: (n+1)! * (n+2)/(n-1)!
Como posso resolver esse exercício: (n+2)!.5!/n!.(n+1)!=0