Olá amigos! Nesta página vamos apresentar vários exercícios resolvidos sobre o Diagrama de Venn, uma ferramenta muito bacana que simplifica e muito a resolução de algumas questões.
Lembrando que os exercícios apresentados foram retirados de provas de concursos públicos aplicadas nos últimos anos.
Bom estudo!
Exercício 1. (CRM ES 2016 – Quadrix) Numa pesquisa, verificou-se que, das pessoas consultadas, 100 se informavam pelo site A; 150 por meio do site B; 20 buscavam se informar por meio dos dois sites, A e B; e 110 não se informavam por nenhum desses dois sites. Desse modo, é correto afirmar que o número de pessoas consultadas nessa pesquisa foi de:
a) 380
b) 360
c) 340
d) 270
e) 230
Resolução
A questão pode ser facilmente resolvida através do Diagrama de Venn.
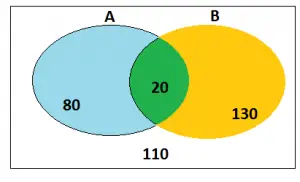
Veja na figura que:
- A região azul corresponde a quantidade de pessoas que se informavam apenas pelo site A (100 – 20).
- A região amarela corresponde a quantidade de pessoas que se informavam apenas pelo site B (150 – 20).
- A região verde corresponde a quantidade de pessoas que se informavam pelos dois sites.
- A região branca corresponde a quantidade de pessoas que não se informavam por nenhum dois dois sites.
O total de pessoas consultadas será:
80 + 20 + 130 + 110 = 340 pessoas
Resposta: C
Exercício 2. (PM PA 2007 – Fadesp) Dos 100 soldados que participavam de um curso de formação de cabos, 40 gostavam de praticar voleibol, 68 gostavam de praticar futebol e 14 não gostavam de praticar esses esportes. A quantidade de soldados que gostavam de praticar tanto voleibol quanto futebol é igual a
(A) 18.
(B) 22.
(C) 30.
(D) 46.
Resolução
Vamos resolver a questão com o auxílio da figura abaixo (Diagrama de Venn), sendo que no círculo vermelho estão os soldados que gostam de voleibol, no verde os que gostam de futebol, e fora dos dois, os que não gostam de nenhum desses esportes.
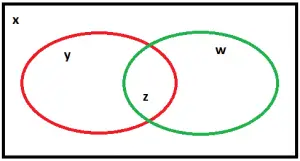
Temos:
x + y + z + w = 100
y + z = 40
z + w = 68
x = 14
Como x = 14, temos que:
x + y + z + w = 100
14 + y + z + w = 100
y + z + w = 100 – 14
y + z + w = 86
Assim, temos 3 equações:
(1) y + z + w = 86
(2) y + z = 40
(3) z + w = 68
Fazendo (1) – (2):
y + z + w – y – z = 86 – 40
y + z + w – y – z = 86 – 40
w = 46
A questão pede para descobrirmos quantos gostam dos dois esportes, ou seja, o valor da letra z. Podemos utilizar a equação 3:
z + w = 68
z + 46 = 68
z = 68 – 46
z = 22
Resposta: B
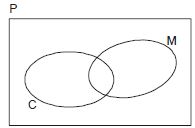
Exercício 3. (Saeb BA 2010 – FCC) Em relação às pessoas presentes em uma festa, foi feito o diagrama abaixo, no qual temos:
P: conjunto das pessoas presentes nessa festa;
M: conjunto dos presentes nessa festa que são do sexo masculino;
C: conjunto das crianças presentes nessa festa.
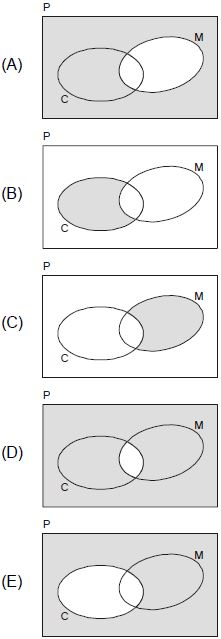
Assinale o diagrama em que o conjunto dos presentes na festa que são do sexo feminino está representado em cinza.
Resolução
Questão simples, basta analisarmos que o círculo M não pode estar pintado e todas as áreas de fora devem estar.
Resposta: A
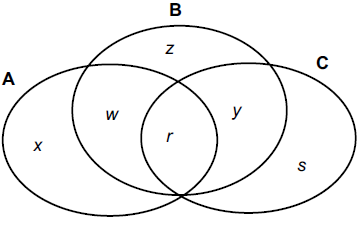
Exercício 4. (TJ SP 2014 – Vunesp) O diagrama mostra a distribuição de pessoas, que possuem uma ou mais das habilidades A, B, C. As letras minúsculas representam o número de pessoas que possuem determinada ou determinadas habilidades. Por exemplo: a letra w, que está na intersecção dos grupos de habilidades A e B, representa a quantidade de pessoas que possuem ambas as habilidades citadas.
Foi realizada uma enquete com todas essas pessoas, e elas deveriam responder SIM ou NÃO a essa única pergunta: “Você possui as habilidades A e C? Todas as pessoas responderam de forma verdadeira, e o número de pessoas que respondeu SIM foi
(A) x + s.
(B) w + r + y.
(C) x + r + s.
(D) zero.
(E) r.
Resolução
Basta verificar no desenho (Diagrama de Venn) que a única área que representa as pessoas que possuem as habilidades A e C ao mesmo tempo é a simbolizada pela letra r.
Resposta: E
Questão 5 (TJ SP – Vunesp 2017). Carlos é o único atleta que tem patrocínio de 3 empresas: A, B e C. Em se tratando de atletas que recebem patrocínios de apenas 2 dessas empresas, temos: Leandro e Hamilton, das empresas A e B; Marta e Silas, das empresas A e C; e Amanda, Renata e Sérgio, das empresas B e C. Se esses atletas fazem parte de um grupo contendo, ao todo, 18 atletas que recebem patrocínio das empresas A, B ou C, e cada empresa tem, pelo menos, 1 atleta recebendo patrocínio somente dela, então é correto afirmar que os números mínimo e máximo de atletas que a empresa B pode patrocinar são, respectivamente,
(A) 8 e 16.
(B) 6 e 12.
(C) 4 e 8.
(D) 5 e 10.
(E) 7 e 14.
Resolução
Vamos montar o Diagrama de Venn, onde x, y e z representam a quantidade de atletas patrocinados apenas pelas empresas A, B e C, respectivamente. Lembrando que x, y e z devem ser, no mínimo, iguais a 1.
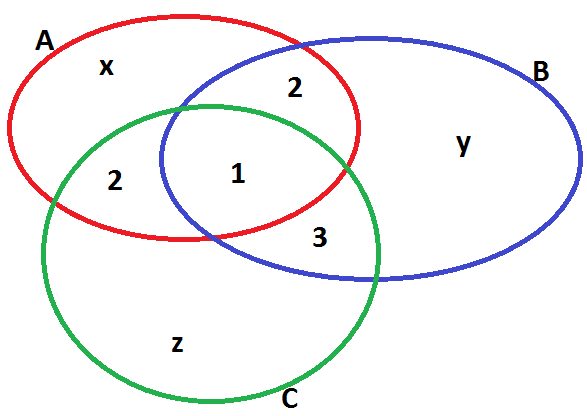
Pelo diagrama, temos que:
x + y + z + 2 + 2 + 3 + 1 = 18
Para que y seja o maior valor possível, devemos considerar x = z = 1.
x + y + z + 2 + 2 + 3 + 1 = 18
1 + y + 1 + 8 = 18
y + 10 = 18
y = 8
Vamos obter o mínimo de pessoas patrocinadas por B considerando y = 1.
2 + 1 + 3 + 1 = 7
Resposta: E
Questão 6 (PM ES – AOCP). 70 soldados se inscreveram em três cursos, em que cada curso é direcionado para uma área de atuação de suas funções: Combate a Incêndio, Busca e Salvamento ou Atendimento Pré-hospitalar. Cada soldado podia optar por se inscrever em um, em dois ou nos três cursos disponibilizados e todos os soldados se inscreveram em pelo menos um dos três cursos oferecidos, da seguinte maneira:
– 59 soldados optaram por cursar Combate a Incêndio;
– 56 soldados optaram por cursar Busca e Salvamento;
– 33 soldados optaram por cursar Atendimento Pré-hospitalar;
– 50 soldados optaram por cursar Combate a Incêndio e Busca e Salvamento;
– 23 soldados optaram por cursar Busca e Salvamento e Atendimento Pré-hospitalar;
– 25 soldados optaram por cursar Atendimento Pré-hospitalar e Combate a Incêndio;
– 20 soldados optaram por cursar as três áreas oferecidas.
Dessa forma, o número de soldados que optaram por cursar somente uma das três áreas de atuação é igual a
A) 7
B) 8
C) 9
D) 10
E) 12
Resolução
Podemos resolver a questão utilizando o Diagrama de Venn.
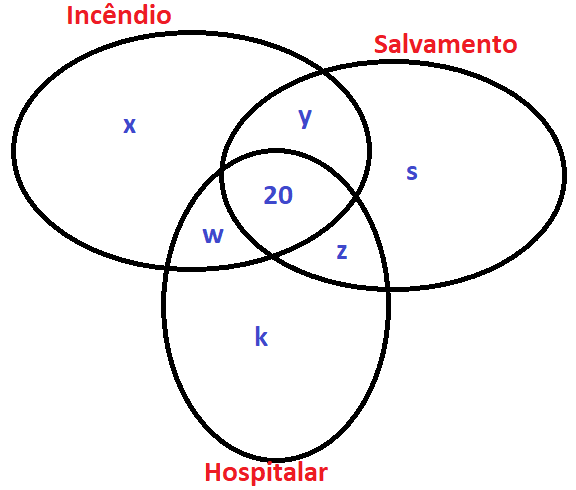
50 soldados optaram por cursar Combate a Incêndio e Busca e Salvamento
y + 20 = 50
y = 50 – 20
y = 30
23 soldados optaram por cursar Busca e Salvamento e Atendimento Pré-hospitalar
20 + z = 23
z = 23 – 20
z = 3
25 soldados optaram por cursar Atendimento Pré-hospitalar e Combate a Incêndio
20 + w = 25
w = 25 – 20
w = 5
Como cada um dos 70 soldados se inscreveu em pelo menos um curso:
x + s + k + y + w + z + 20 = 70
x + s + k + 30 + 5 + 3 + 20 = 70
x + s + k + 58 = 70
x + s + k = 70 – 58
x + s + k = 12
Veja no diagrama que x + s + k representa a quantidade de soldados que se inscreveu em apenas um curso.
Resposta: E
Gostou dos nossos exercícios resolvidos sobre o Diagrama de Venn?
Deixe o seu comentário.

Essa última questão não entendi. Poderia fazer um vídeo simples dessa questão? Eu fiz essa prova e até agr não entendi. Pq eu tenho que transformar o x e z em 1????
Olá Yedda!
Farei assim que possível.
Obrigado por acessar nosso site.
Olá,descobri um jeito bem mais rápido e eficaz para a questão número 2:
Vamos usar as mesmas variáveis apontadas pelo professor.
X+y+Z+W=100
14+Y+Z+W=100
Y+Z+W=86.
Descobrimos que a soma dos soldados que fizeram alguma das duas atividades descrita pelo enunciado é 86, então vamos substituir as variáveis pelos números cultos no enunciado:
Y+Z+W=86=46+Z+W=86=Z+W=86-46=40
ENTÃO A EQUAÇÃO FICA: Z+W=40
Substituimos O W pelo 18:
Z+18=40
Z=40-18
Z=22
Tenho algo a complementar. Percebi que a forma de fazer, tem jeitos mais fáceis (dps que fiz vários exercicios sobre isso); por exemplo, no Exercício 2, vi que você fez muitos cálculos, e sinceramente, me perdi toda na primeira vista, achei mais complicado dessa maneira. Tem outras duas formas de fazer, que pelo que vi pode ser utilizado em outras problemas desse mesmo tipo: A+B-A∩B+C=100 (40+68-A∩B+14=100 / 122-A∩B=100 / A∩B=22. Tem este tbm mais fácil: 40-z+z+68-z+14=100 (ai faz o cálculo). Agradeço por esse site, no comentário acima que fiz, eu ainda estava mais leiga no assunto, e agora estou mais aprofundada. Entendi perfeitamente este último problema, mas não estava interpretando a forma que você fez a resolução. Tentei sozinha e entendi. Muito obrigada!
Boa tarde! Favor, preciso da sua ajuda para resolver uma questão de probabilidade que tem me dado voltas.
Dos trabalhadores de uma empresa que utilizam regularmente os transportes públicos, sabe-se que 54% utilizam exclusivamente um destes meios de transporte: autocarro (22%), metropolitano (25%) ou comboio (7%).
44% utilizam pelo menos dois daqueles três meios de transporte: 18% utilizam o autocarro e metropolitano, 17% utilizam o autocarro e o comboio, 19% utilizam o metropolitano e o comboio.
a) tendo presente que existem outros meios de transporte público, qual a percentagem de trabalhadores que não utilizam qualquer um destes meios para o trabalho?
b) qual a percentagem de trabalhadores que utilizam os três meios de transporte na sua deslocação para o trabalho?
Respostas: a) 0.02 b) 0.05.
A alinha a) já consegui. Quanto a b) não consigo determinar. Agradeço ajuda. Estou me preparando para um exame.
Obrigado.
Boa Tarde,
Ótimo post, porém gostaria de fazer uma correção.
A resposta do exercício 4 está como a letra E), onde a intersecção dos conjuntos A e C seria “r”. Entretanto, “r” representa a intersecção de todos os conjuntos (A, B e C), não havendo nenhum representante da intersecção dos conjuntos A e C no diagrama apresentado. Desta forma, a resposta correta dessa questão seria a letra D) ZERO.
Abraços.
Olá Mariana!
Temos que nos concentrar na pergunta “Você possui as habilidades A e C?”
Veja que quem está em r certamente respondeu a pergunta com um Sim.
O seu raciocínio estaria correto se a pergunta fosse “Você possui apenas as habilidades A e C?”
Obrigado pela contribuição.
Sucesso!
Olá Jordon,
Nossa!! Muito obrigada pelo esclarecimento e pela pronta resposta (que só vi agora!)
Sim, de fato não me atentei a pergunta. Entendi o raciocínio agora!
Ótimo blog!! 😀
Até mais!
É verdade Mariana, você tem razão!!É muito fácil comprovar a sua afirmativa, pois se colocarmos um eixo na intersecção onde se localiza o r, veremos que B também esta intersectado!!
Peço a vossa ajuda pra resolver esta questão
Perguntaram a 165 alunos duma Escola Secundária sobre as suas preferências musicais e o resultado foi o seguinte:
65 alunos gostavam de Marabenta
74 gostavam de música afrojazz
63 não gostavam desses dois tipos músicais
A) Quantos alunos gostam de marrabenta ou afrojazz?
B) Quantos gostam dos dois tipos?
C) Represente num diagrama de Venn.
37 gostam dos dois tipos
Peço a vossa a juda.
Numa pesquisa feita na Província de Maputo, constatou-se que num universo de 100 jovens, 10 tem casa propria, 8 tem casa própria e carro e, 22 não tem casa nem carro.
A) Represente os dados num diagrama de Venn
B) Quantos jovens têm somente carro?
100 = 22+2+8+(X-8)
100 = 32+X-8
100 = 24+X
X = 100-24
X = 76
APENAS CARRO: X-8 = 76-8 = 68
boa tarde apenas não sei desenhar o diagrama, mas segue a resolução: universo = 100, não casa(C) e carro(K) =22, ou seja 100-22=78
segundo passo casa(C) e carro(K)=8, ou seja apenas casa C= 2
terceiro passo achar apenas carro(K) 8+2+K= 78
K=68, ou seja 68 tem apenas carro.
Bom dia peço ajuda: Numa escola 30 professores lecionam no periodo de manha, 25 lecionam a tarde e 5 lecionam nos dois periodos, representa dos dados num diagrama de veen. quantos professores lecionam num so periodo?
300 alunos de uma escola foram entrevistados a respeito de três frutos: Morango, uva e abacaxi.
O resultado foi o seguinte:
160 gostam de comer Morango;
120 gostam de comer uva;
80 gostam de comer abacaxi;
30 gostam de comer morango e uva;
40 gostam de comer uva e abacaxi;
40 gostam de comer morango e abacaxi;
10 gostam de comer os três frutos.
Utilizando o diagrama de Venn, Calcule quantos alunos não gostam de comer nenhum dos três frutos.
A 40
B 50
C 60
D 70
E 80
Me ajudem a achar a resposta Prfv
simplesmente dez amei irmao, mantenha o site , ele é otimo parabéns.
Questão 2 eu encontrei rapidamente a resposta somando tudo ! ( voleibol ) 40 + 68 (futebol) +14 = 122, peguei o número de pessoas que gostam dos 2 esportes e de que não gosta de nenhum deles e diminui pelo numero total de pessoas 100, resultado 22. B
Em uma sala com 50 alunos, 30 leram o Livro: Memórias Póstumas de Brás Cubas, de Machado de Assis, 17 leram somente o Livro: Senhora, de José de Alencar, 3 não leram nenhum dos livros. Dois alunos tentaram representar essa situação por diagrama de Venn, onde “M” foi o nome dado ao conjunto que indica o livro escrito por Machado de Assis e “S” o nome dado ao conjunto que indica o livro escrito por José de Alencar. Analise os diagramas a seguir e determine o correto. Depois indique o valor de x, no diagrama correto.
O diagrama A{ 30-x(x)17-x}. B={30-x(x)17 }
{Nenhum 3 }. {Nenhum 3}
() O valor de x é 5
() O valor de x é 2
() O valor de x é – 2
() O valor de x é zero
() Os dois alunos erraram, logo não existe alternativa correta
Olá, eu acho que você representou a equação errada o certo não seria A{30-X+X+17-X}?
Olá Newton,
Está se referindo a qual questão?
tenho uma duvida na questão 6:
se
SI=SÓ INCENDIO
SH=SÓ HOSPITAL
SS=SÓ SALVAMENTO
IS=INCENDIO E SALVAMENTO=50
SH=SALVAMENTO E HOSPITAL =23
HI=HOSPITAL E INCENDIO=25
HIS=AS 3 AREAS=20
I=SI+HI+HIS+IS
59=SI+25+20+50
59-25-30-50=SI
SCI=-43?
S=SS+IS+HIS+SH
56=SS+50+20+23
56-50-20-23=SS
SS=-37?
H=SH+SH+HIS+HI
33=SH+23+20+25
33-23-20-25=SH
SH=-35?
não consigo colar o diagrama, mas aprece não ser possível esses valores
Obrigado por compartilhar.
Muito bom esse material, para não dizer excelente.
questão 2: x são os soldados que praticam os dois esportes, então: 68-x+x+40-x+14=100
-x+122=100 -x=100-122 -x=-22 x=22