Procurando exercícios resolvidos sobre áreas de figuras planas?
Chegou ao site certo.
Confira exercícios resolvidos retirados de diversas provas de concursos realizadas por todo o país.
Bons estudos.
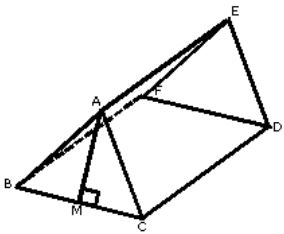
Questão 1 (PM Pará 2012). A figura abaixo mostra um telhado de uma casa, onde AB = AC, BC = 4 m, AM = 1,5 m, CD = BF = 15 m e M é o ponto médio de BC. Considerando que para cobrir um metro quadrado de telhado são utilizadas 16 telhas, a quantidade de telhas para cobrir esse telhado será de:
a) 800
b) 900
c) 1000
d) 1200
e) 1500
Resolução:
Primeiramente vamos calcular a medida de AC:
Como AB = AC e M é ponto médio de BC, temos que AMC é um triângulo retângulo, onde AC é a hipotenusa, MC = 2 pois BC = 4 e AM = 1,5.
Utilizando o Teorema de Pitágoras:
AC² = MC² + AM²
AC² = 2² + 1,5²
AC² = 4 + 2,25
AC² = 6,25
AC = 2,5m
Agora vamos calcular a área de um dos lados do telhado, depois multiplicar por 2:
Área = AC.CD = 2,5.15 = 37,5m²
2.37,5 = 75m²
Como cada m² equivale a 16 telhas:
16.75 = 1200
Resposta: D
Questão 2 (PM Pará 2012). Um empresário possui um espaço retangular de 110 m por 90 m para eventos. Considerando que cada metro quadrado é ocupado por 4 pessoas, a capacidade máxima de pessoas que esse espaço pode ter é:
a) 32.400
b) 34.500
c) 39.600
d) 42.500
e) 45.400
Resolução:
Vamos calcular a área do espaço:
A = 90 x 110 = 9900 m²
Como cabem 4 pessoas por m²:
Capacidade = 4.9900 = 39600
Resposta: C
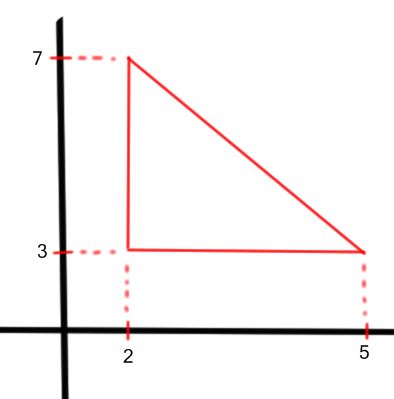
Questão 3 (PM Pará 2012). Os pontos (2,3), (5,3) e (2,7) são vértices de um triângulo retângulo. A área desse triângulo é:
a) 5 u.a
b) 6 u.a
c) 7 u.a
d) 8 u.a
e) 9 u.a
Resolução:
Veja no desenho como fica o triângulo:
Fórmula para cálculo de área de um triângulo:
A = base x altura / 2
base = 5 – 2 = 3
altura = 7 – 3 = 4
A = 3.4/2 = 6
Resposta: B
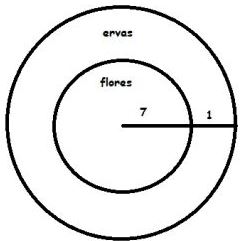
Questão 4 (CFO PM ES 2013 – Exatus). Adriana planta flores num canteiro circular de raio 8 m. Ao redor desse canteiro, ela pretende plantar ervas medicinais formando uma coroa circular, de maneira que a parte destinada às flores sofrerá uma redução de 2 m em seu diâmetro. A área ocupada pelas ervas medicinais neste canteiro será igual a:
a) 14π
b) 12π
c) 5π
d) 15π
Resolução:
Adriana planta em um circulo de raio 8, de onde podemos concluir que o diâmetro mede 16 metros.
Se reduzirmos o diâmetro em 2 metros, passando a medir 14 metros, o raio passará a medir 7 metros.
Assim, a área da coroa circular será a diferença entre a área do circulo de raio 8 e do circulo de raio 7 (Área circunferência = π.r²):
π.8² – π.7² = 64π – 49π = 15π
Resposta: D
Questão 4 (PM ES 2013 – Funcab). Um para-raios instalado em um determinado prédio protege uma área circular de raio R = 20 m no solo. O valor total da área do solo, em metros quadrados, protegida por esse para-raios, é de:
(Adote o valor aproximado de π= 3,14)
A) 1.256 m²
B) 1.294 m²
C) 1.306 m²
D) 1.382 m²
E) 1.416 m²
Resolução:
Calculando a área do círculo:
Área = π . r²
Área = 3,14 . 20²
Área = 3,14 . 400
Área = 1256
Resposta: A
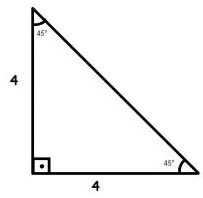
Questão 5 (PM Acre Músico 2012 – Funcab). A área de um triângulo isósceles cujos lados iguais medem 4, e dois de seus ângulos medem 45º, corresponde a:
A) 4 u.a.
B) 8 u.a.
C) 12 u.a.
D) 16 u.a.
E) 20 u.a.
Resolução:
Temos um triângulo retângulo (o valor da altura e da base é 4).
A = base x altura / 2
A = 4×4/2
Resposta: B
Questão 6 (Correios 2011 – Cespe). Em 2008, nos 200 anos do Banco do Brasil, os Correios lançaram um selo comemorativo com uma tiragem de 1.020.000 unidades. No selo, cujo formato é de um retângulo medindo 40 mm × 30 mm, a estampa ocupa um retângulo que mede 35 mm × 25 mm. Dadas essas condições, é correto afirmar que a área do retângulo da estampa é
A. superior a 90% da área do retângulo do selo.
B. inferior a 75% da área do retângulo do selo.
C. superior a 75% e inferior a 80% da área do retângulo do selo.
D. superior a 80% e inferior a 85% da área do retângulo do selo.
E. superior a 85% e inferior a 90% da área do retângulo do selo.
Resolução:
Como estamos trabalhando com porcentagem, não há necessidade de utilizar a medida mm.
Basta dividirmos a área da estampa pela área do selo. Veja:
Resposta: B
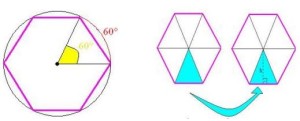
Questão 7 (PM Paraná 2010 – Cops). Considere uma placa de trânsito na forma de um hexágono regular com lados de L centímetros. Sabe-se que um hexágono regular de lados L é formado por seis triângulos equiláteros de lados L. Como a leitura desta sinalização (placa) depende da área A da placa, temos que A, em função do comprimento L, é dada por:
Resolução
Aplicando o Teorema de Pitágoras, vamos descobrir a altura h do triângulo para descobrirmos sua área:
l² = h² + (l/2)²
l² – l²/4 = h²
(4l² – l²)/4 = h²
3l²/4 = h²
h = l√3/2
Calculando a área:
A∆ = l . l√3/2/2
A∆ = l² √3 /4
A área do hexágono regular será igual a 6 vezes a área do triângulo equilátero.
A = 6 . l² √3/4
A = 3 l² √3 / 2
Resposta: B
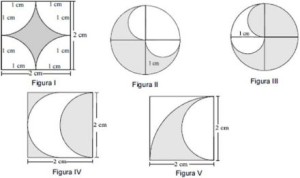
Questão 8 (PRF 2008 – Cespe). Considerando, em relação às figuras abaixo, que, na figura I, as 4 curvas são quartos de circulo; nas figuras II, III e IV, as curvas são 2 semicírculos; na figura V, aparece 1 quarto de círculo e, interno a ele, um semicírculo, nessa situação, as figuras em que as partes sombreadas têm áreas iguais são:
b) I e V.
c) II e III.
d) II e V.
e) III e IV
Resolução
Figura I:
Temos um quadrado com 4 semicírculos inscritos, que resultam em um círculo completo. Então a área sombreada será a área do quadrado menos a área do círculo com raio de 1 cm. Calculando as áreas:
1. Área do quadrado: 2 x 2 = 4 cm²;
2. Área do círculo: ∙π 1² = π cm²;
3. Área sombreada: 4 – π.
Figura II:
A área sombreada é formada por 3/4 da área de um círculo com raio de 1 centímetro, menos a área de 2 semicírculos de raio igual a 1/2 centímetro. Lembre que dois semicírculos formam um círculo. Então:
1. Área do círculo com raio de 1 cm: π 1² = π cm²;
2. 3/4 da área do círculo anterior: 3π/4
3. Área do círculo com raio igual de 1/2 cm: π.(1/2)² = π/4
4. Área sombreada: 3π/4 – π/4 = 2π/4 = π/2cm².
Figura III:
Se o semicírculo sombreado trocar de lugar com o semicírculo brando, a área sombreada será igual a 3/4 da área do círculo de raio de 1 cm. Veja:
1. Área do círculo de raio de 1 cm: π1² = π cm²;
2. Área sombreada: 3π/4 cm².
Figura IV
Se encaixarmos o semicírculo sombreado no semicírculo branco, têm-se um retângulo com a metade sombreada e a outra branca. Dessa forma, a área sombreada seria igual a metade da área de um retângulo de 2 x 2. Veja:
1. Área sombreada: 2.2/2 = 2 cm².
Figura V:
A área sombreada será obtida com a subtração da área de um quarto de círculo de raio igual a 2 centímetro pela metade de um semicírculo de raio igual a 1 centímetro. Calculando as áreas:
1. Área de 1/4 de círculo de 2 cm de raio: π2²/4 = πcm².
2. Área de um semicírculo de 1 cm de raio: π1²/2 = π/2cm².
3. Área sombreada: π – π/2 = π/2 cm².
Resposta: D
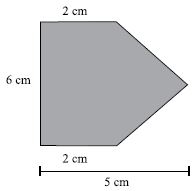
Questão 9 (SAP SP 2013). Ricardo esteve em um lançamento imobiliário onde a maquete, referente aos terrenos, obedecia a uma escala de 1:500. Ricardo se interessou por um terreno de esquina, conforme mostra a figura da maquete.
A área, em metros quadrados, desse terreno é de
(A) 300.
(B) 755.
(C) 120.
(D) 525.
(E) 600.
Resolução
Primeiramente, vamos utilizar a escala 1:500 para sabermos as dimensões reais do terreno:
2cm equivale a 2.500 = 1000cm = 10m
6cm equivale a 6.500 = 3000cm = 30m
5cm equivale a 5.500 = 2500cm = 25m
Sabendo disto, para calcularmos a área é muito simples, basta dividirmos a figura em duas, um retângulo e um triângulo:
O retângulo terá base 30m (6cm) e altura 10m (2cm):
Área = 30×10 = 300m²
O triângulo terá base 30m (6cm) e altura 15m (3cm):
Área = 30×15/2 = 225m²
Área total = 300 + 225 = 525m²
Resposta: D

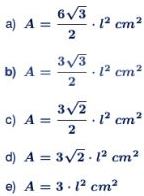
determine a area de um triangulo retangulo tal que a soma das medidas dos catetos e igual a 28 cm e a soma dos quadrados das medidas dos tres lados e igual a800 cm²
A questão que diz respeito ao jardim parece estar errada. A questão nos da um raio de 8 cm, e diz que é retirado 2cm. Como ficaria com 7 ?
Olá Ana,
Uma típica pegadinha que confunde bastante.
A questão fala que o RAIO é 8 e o DIÂMETRO é reduzido em 2, ou seja, o RAIO é reduzido em 1.
Bons Estudos.
3 anos depois …
Pelo que eu entendi, RAIO = 8 , LOGO O DIÂMETRO = 16. TENHO D= 16 -2 = 14, R=7 OU R= 8-1
RAIO = 8 , LOGO O DIÂMETRO = 16. TENHO D= 16 -2 = 14, R=7 OU R= 8-1
quantas e quais sao as formulas utilizadas para calcular area de figuras planas?
Olá Kryslany!
Você encontrará as fórmulas na sessão “Material Didático”.
ou valeu tu me salvou, eu nao estava entendo nada agora sei quase tudo
Uma quadra de futebol foi construída com as seguintes dimensões: 10 metros de largura e 20 metros de
comprimento, conforme a figura abaixo. Obteve-se por círculo central (região circular no centro da quadra),
um círculo C de raio 2 metros e, por áreas (regiões nas quais os goleiros podem tocar a bola com as mãos),
dois semicírculos, S1 e S2, de raio 4 metros.
Essa quadra será reformada, aumentando-se, proporcionalmente, seu comprimento e sua largura, mas
mantendo-se inalterados os raios de C, S1 e S2, de tal modo que o percentual ocupado pela soma das áreas
de C, S1 e S2 seja igual a 10% da área da nova quadra.
Usando = 3 e √ = 1,7, é CORRETO afirmar que a diferença entre o novo comprimento e a nova largura
dessa quadra será, em metros, de
Um engenheiro de férias em seu sítio, ao sair para um passeio habitual, se depara com um velho problema de suas caminhadas, um grande barranco. Este obstáculo sempre o faz aumentar seu trajeto, o que o deixa cansado e o impede de aproveitar o por do sol acima dos morros da região. Compenetrado em se ver de vez livre deste problema, decide construir uma ponte que o poupe do desvio de seu caminho. O primeiro passo é medir a distância entre um lado e outro do barranco para comprar os materiais necessários. No entanto, justamente o buraco o impede de medi-lo. Justamente onde termina o barranco, onde ele geralmente contorna o barranco para continuar sua caminhada, há uma árvore. Ele percebe que essa árvore poderá formar um triangulo, tendo a distância de um lado e outro do buraco como um de seus lados. A distância de cada ponta do barranco até a árvore é de 60 m.
Como o engenheiro deverá proceder para descobrir a distância entre um lado e outro do barranco?