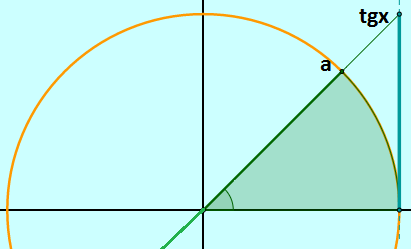
As equações trigonométricas costumam “dar um nó” na cabeça de muitos estudantes. Nesta página vamos aprender a resolvê-las através da resolução das equações trigonométricas fundamentais.
Pede-se que o aluno tenha um conhecimento avançado sobre o ciclo trigonométrico, arcos, seno, cosseno e tangente.
Bom estudo!
Definição
Uma equação é dita trigonométrica quando a incógnita representa um arco. Veja:
- Exemplos de equações trigonométricas:
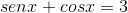
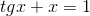
- Exemplos de equações não trigonométricas:
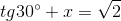
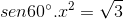
Você já deve ter notado que as equações trigonométricas não possuem um modelo pré definido, como, por exemplo, uma equação do segundo grau. E justamente por este motivo, não existe um único e infalível método que possa ser utilizado para resolver todas elas.
O que podemos fazer e manipulá-las, transformando-as em equações mais simples e equivalentes. São as chamadas equações trigonométricas elementares ou equações trigonométricas fundamentais. São elas:
a) sen(x) = sen(a)
b) cos(x) = cos(a)
c) tg(x) = tg(a)
Lembrando que a∈R e x é a incógnita.
Vamos agora aprender a resolver cada uma das três equações.
Resolução da equação fundamental sen(x) = sen(a)
Para que x e a tenham o mesmo seno, basta que suas extremidades coincidam ou sejam simétricas em relação ao eixo dos senos.
Nessas condições, podemos afirmar que os arcos abaixo possuem o mesmo seno, onde k∈Z e representa a quantidade de voltas no ciclo trigonométrico no sentido horário, se positivo, ou a quantidade de voltas no sentido anti horário, se negativo.
- a+2kπ
- (π-a) + 2kπ
Veja como fica o conjunto solução:
S = {x∈R | x = a + 2kπ ou x = (π-a) + 2kπ, k∈Z}
Exemplo 1
Resolver a equação senx = sen(π/5)
Temos:
x = π/5 + 2kπ, k∈Z
ou
x = (π – π/5) + 2kπ = 4π/5 + 2kπ, k∈Z
Conjunto solução:
S = {x∈R | x = π/5 + 2kπ ou x = 4π/5 + 2kπ, k∈Z}
Resolução da equação fundamental cos(x) = cos(a)
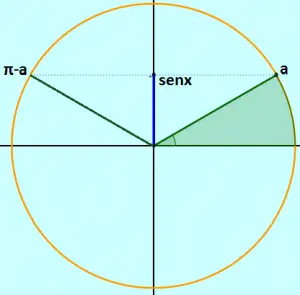
Para que x e a tenham o mesmo seno, é necessário e suficiente que suas extremidades coincidam ou sejam simétricas em relação ao eixo dos cossenos.
Podemos afirmar que os arcos abaixo possuem o mesmo cosseno, onde k∈Z e representa a quantidade de voltas no ciclo trigonométrico no sentido horário, se positivo, ou a quantidade de voltas no sentido anti horário, se negativo.
- a+2kπ
- -a + 2kπ
Podemos representar o conjunto solução da seguinte forma:
S = {x∈R | x = a + 2kπ ou x = (π-a) + 2kπ, k∈Z}
Exemplo 2
Resolver a equação cosx = cos(π/3)
Temos:
x = π/3 + 2kπ, k∈Z
ou
x = -π/3 + 2kπ, k∈Z
Conjunto solução:
S = {x∈R | x = π/3 + 2kπ ou x = -π/3 + 2kπ, k∈Z}
Resolução da equação fundamental tg(x) = tg(a)
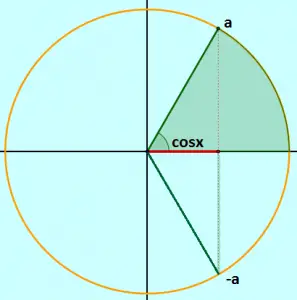
Na tangente também temos dois casos: ou as extremidades de x e a são coincidentes, ou são simétricas em relação do centro do ciclo trigonométrico.
Podemos afirmar que os arcos abaixo possuem a mesma tangente, onde k∈Z e representa a quantidade de voltas no ciclo trigonométrico no sentido horário, se positivo, ou a quantidade de voltas no sentido anti horário, se negativo.
- a+2kπ
- (a+π) + 2kπ
Podemos representar o conjunto solução da seguinte forma:
S = {x∈R | x = a + 2kπ ou x = (a+π) + 2kπ, k∈Z}
Exemplo 3
Resolver a equação tgx = 1
Como já é sabido, tg(π/4) = 1.
Temos:
x = π/4 + 2kπ, k∈Z
ou
x = (π/4+π) + 2kπ = 5π/4 + 2kπ, k∈Z
Conjunto solução:
S = {x∈R | x = π/4 + 2kπ ou x = 5π/4 + 2kπ, k∈Z}
Como as soluções são simétricas em relação ao centro, o conjunto solução também pode ser simplificado da seguinte forma:
S = {x∈R | x = π/4 + kπ, k∈Z}
Como já foi dito, não existe uma fórmula pronta para a resolução das equações trigonométricas. O estudante deve analisar bem a equação e tentar chegar em uma das equações fundamentais. Vamos resolver um exemplo onde isto acontece:
Exemplo 4
Resolver a equação senx + cosx = 1.
Elevando ambos os membros ao quadrado:
(senx + cosx)² = 1²
(senx)² + 2.senx.cosx + (cosx)² = 1
(senx)² + (cosx)² + 2.senx.cosx = 1
Utilizando a relação fundamental da trigonometria:
1 + 2.senx.cosx = 1
2.senx.cosx = 0
sen(2x) = 0
Daí,
2x = kπ, k∈Z
x = k.(π/2), k∈Z
Para finalizar, devemos ainda verificar se existem raízes estranhas, considerando que inicialmente elevamos ambos os membros ao quadrado.
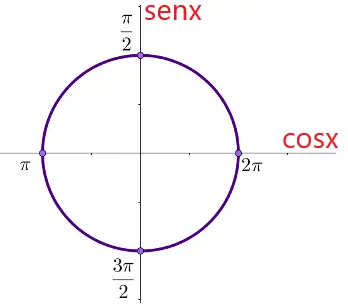
Observando o círculo trigonométrico, as raízes encontradas foram 0, π/2, π, 3π/2, 2π, …
Analisando as raízes, é possível verificar que π e 3π/2 não são raízes da equação, assim, o conjunto solução será:
x = 2kπ ou x = π/2 + 2kπ, k∈Z.
Gostou da nossa publicação sobre equações trigonométricas?
Deixe o seu comentário.