Dando continuidade ao estudo da geometria analítica, nesta página apresentaremos o estudo da equação reduzida da reta.
Considere estudar primeiro os nossos conteúdos sobre plano cartesiano e equação do primeiro grau.
Bom estudo!
Uma reta no plano cartesiano pode ser representada por diversas formas. Nesta página veremos como é feita a representação através da chamada equação reduzida da reta, a saber:
y = m.x + n
Onde:
x e y são as coordenadas dos pontos pertencentes à reta
m é o coeficiente angular da reta
n é o coeficiente linear
Exemplo 1
y = 2x + 1
Veja que o coeficiente angular é igual a 2, enquanto o coeficiente linear é igual a 1.
Exemplo 2
y = -x + 10
Veja que o coeficiente angular é igual a -1, enquanto o coeficiente linear é igual a 10.
Exemplo 3
y = -x
Temos que o coeficiente angular é igual a -1 e o coeficiente linear é igual a 0.
Mas qual é o objetivo de estudar o coeficiente angular e o coeficiente linear?
Eles nos fornecem informações importantíssimas sobre o posicionamento da reta no plano cartesiano. Veja:
Coeficiente angular
O coeficiente angular (m) nos informa a inclinação da reta em relação ao eixo x.
Neste caso temos que tgα = m, onde α é o ângulo formado entre a reta e o eixo x.
Coeficiente linear
O coeficiente linear (n) nos informa o ponto em que a reta intercepta o eixo y.
Neste caso temos que as coordenadas deste ponto são (0, n).
A figura abaixo apresenta as informações fornecidas pelos coeficientes angular e linear.
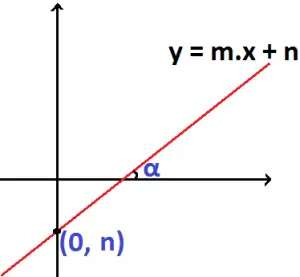
DETERMINANDO A EQUAÇÃO REDUZIDA DA RETA A PARTIR DE DOIS PONTOS
A maneira mais simples de se determinar a equação reduzida da reta é determinar o coeficiente angular e utilizá-lo para determinar o coeficiente linear. Veja o exemplo:
Exemplo 4. Determinar a equação reduzida da reta que passa pelos pontos A(2, 3) e B(-1, -3).
Sabendo que a reta passa pelos pontos A e B, é possível traçá-la no plano cartesiano. Nosso objetivo será descobrir a sua inclinação (m) e o ponto onde passa pelo eixo y (n).
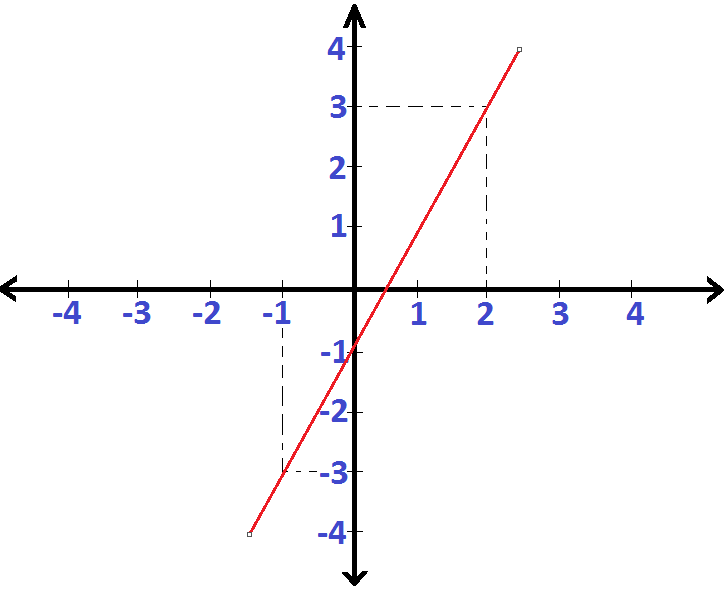
Determinando o coeficiente angular
Sabendo as coordenadas dos pontos A e B, é possível calcular o coeficiente angular através da seguinte fórmula:
![]()
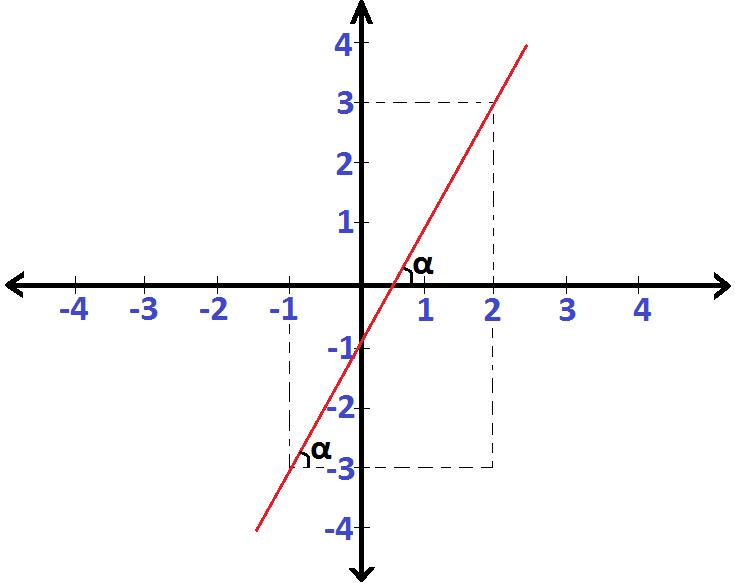
Observando a figura acima, temos que:
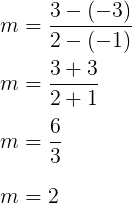
Determinando o coeficiente linear
Vimos que a equação reduzida da reta é do tipo y = mx + n. Como já descobrimos o valor de m, temos que a equação pode ser escrita como y = 2x + n.
Para descobrimos o valor de n, vamos utilizar qualquer um dos pontos conhecidos, que nos fornecerão valores de x e y.
Podemos escolher entre A(2, 3) e B(-1, -3). Como ambos nos levarão ao mesmo resultado, vamos utilizar o ponto A.
No ponto A temos x = 2 e y = 3.
y = 2x + n
3 = 2.2 + n
3 = 4 + n
n = 3 – 4
n = -1
Conclusão: O coeficiente linear é igual a -1, ou seja, a reta passa pelo eixo y no ponto (0, -1).
Gostou do nosso conteúdo sobre a equação reduzida da reta?
Deixe o seu comentário e compartilhe nas redes sociais.
