Você sabe resolver uma equação do 2º (segundo) grau? Veremos aqui as características deste tipo especial de equação, métodos de resolução e vários exemplos.
Bom estudo!
O que é uma equação do 2º grau?
Uma equação é dita do segundo grau ou quadrática quando a incógnita está elevada a um expoente de grau 2.
A forma geral da equação do 2º grau é:
a.x² + b.x + c = 0
Onde:
- x é a incógnita
- a, b e c são as constantes
A única restrição é que a não ode ser igual a zero. Claro né, pois se fosse, não teríamos uma equação do segundo grau e sim do primeiro grau.
Exemplo 1
x² + 5x + 1 = 0
x é a incógnita
a = 1
b = 5
c = 1
Exemplo 2
0,5x² + 6x + 7 = 0
x é a incógnita
a = 0,5
b = 6
c = 7
Exemplo 3
2x² – 6x = 0
x é a incógnita
a = 2
b = -6
c = 0
Exemplo 4
5k² – 9 = 0
k é a incógnita
a = 5
b = 0
c = – 9
Exemplo 5
5t² = 0
t é a incógnita
a = 5
b = 0
c = 0
Como resolver uma equação do 2º grau incompleta
A constante “a” é a única que não pode ser igual a zero. Quando temos b ou c igual a zero, dizemos que a equação é incompleta.
- Quando c = 0
As equações do 2º grau incompletas com c = 0 possuem o seguinte formato:
ax² + bx = 0
Podemos resolver equações com este formato colocando x em evidência:
ax² + bx = 0
x (ax + b) = 0
Observe que um produto é igual a zero quando um de seus termos é igual a zero, ou seja, x = 0 ou (ax + b) = 0.
Daí, a solução será:
x = 0
ou
ax + b = 0
ax = -b
x = -b/a
O conjunto solução será S = {0, -b/a}
Exemplo
x² + 4x = 0
x(x + 4) = 0
Daí,
x = 0
ou
x + 4 = 0
x = – 4
S = {-4, 0}
- Quando b = 0
As equações do 2º grau incompletas com b = 0 possuem o seguinte formato:
ax² + c = 0
Podemos resolver este tipo de equação isolando a incógnita:
ax² + c = 0
ax² = -c
x² = -c/a
x = ±√(-c/a)
O conjunto solução será S = {√(-c/a), -√(-c/a)}
Exemplo
2x² – 18 = 0
2x² = 18
x² = 18/2
x² = 9
x = ±√9
x = ±3
S = {-3, 3}
A fórmula de Bhaskara
As equações do segundo grau completas são resolvidas com mais agilidade através da famosa fórmula de Bhaskara.
Veja como:
Seja a equação do segundo grau ax² + bx + c = 0.
Primeiro calculamos o valor de Δ (delta), onde:
Δ = b² – 4ac
Depois calculamos as raízes através da fórmula:
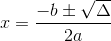
Exemplo
Resolver a equação x² + 2x – 3 = 0.
As constantes são:
a = 1
b = 2
c = – 3
Calculando o valor de Δ:
Δ = b² – 4ac
Δ = 2² – 4.1.(-3)
Δ = 4 + 12
Δ = 16
Calculando as raízes:
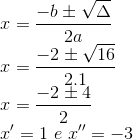
S = {-3, 1}.
A importância do valor de Delta
É importante citar que Δ informa quantas raízes reais a equação do segundo grau possui. Veja:
- Se Δ<0, a equação não possui raízes reais.
- Se Δ=0, a equação possui apenas uma raiz real.
- Se Δ>0, a equação possui duas raízes reais.
O método da soma e produto
Algumas equações do 2º grau podem ser resolvidas através deste método. O seu objetivo é agilizar a resolução, evitando todos os cálculos utilizados na fórmula de Bhaskara.
Considerando a equação do segundo grau geral ax² + bx + c = 0, temos que:
A soma das raízes é sempre -b/a.
O produto das raízes é sempre c/a.
Exemplo
Resolver a equação x² – 5x + 6 = 0
A soma das raízes será:
S = -b/a = -(-5/1) = 5
P = c/a = 6/1 = 6
Neste caso não é difícil perceber que os dois números cuja soma é igual a 5 e o produto é igual a 6 são os números 2 e 3.
S = {2, 3}
Aprendeu a resolver uma equação do 2º grau? Não se esqueça de acessar a sessão com exercícios resolvidos. Aproveite também para compartilhar nas redes sociais e deixar seu comentário no final da página.
