Confira aqui a resolução comentada da questão 145 (volume e porcentagem) do caderno amarelo, matéria de MATEMÁTICA E SUAS TECNOLOGIAS.
Bom estudo!
Questão 145. Um processo de aeração, que consiste na introdução de ar num líquido, acontece do seguinte modo: uma bomba B retira o líquido de um tanque T1 e o faz passar pelo aerador A1, que aumenta o volume do líquido em 15%, e em seguida pelo aerador A2, ganhando novo aumento de volume de 10%. Ao final, ele fica armazenado num tanque T2, de acordo com a figura.
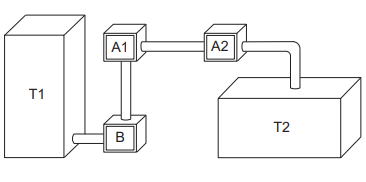
Os tanques T1 e T2 são prismas retos de bases retangulares, sendo que a base de T1 tem comprimento c e largura L, e a base de T2 tem comprimento c/2 e largura 2L.
Para finalizar o processo de aeração sem derramamento do líquido em T2, o responsável deve saber a relação entre a altura da coluna de líquido que já saiu de T1, denotada por X, e a altura da coluna de líquido que chegou a T2, denotada por y.
A equação que relaciona as medidas das alturas y e x é dada por
A) y = 1,265x
B) y = 1,250x
C) y = 1,150x
D) y = 1,125x
E) y = x
Resolução
Considerando que o líquido que saiu de T1 possui altura x, e sabendo o comprimento (c) e a largura (L) de T1, podemos calcular o volume do líquido em T1:
VT1 = x.c.L
Ao passar pelos aeradores A1 e A2, o volume tem um acréscimo de 15% e 10%, respectivamente. Com essas alterações, o volume passará a ser de:
Valterado = x.c.L . 115% . 110%
Valterado = x.c.L . 1,15 . 1,10
Valterado = x.c.L . 1,265
Quando o líquido alterado chegar ao tanque T2, que tem comprimento c/2 e largura 2L, ele estará com altura y, ou seja, o volume em T2 poderá ser calculado da seguinte forma:
VT2 = y . (c/2) . 2L
VT2 = y.c.L
Considerando que o líquido teve o volume alterado e foi despejado em T2, podemos igualar os volumes:
VT2 = Valterado
y.c.L = x.c.L . 1,265
y = 1,265x
Resposta: A
